设（X, Y)~N（1,2;4,9;0.2)，则X服从A．N(1,9)B．N(1,2)C．N(2,9)D．N(1,4)

题目

设（X, Y)~N（1,2;4,9;0.2)，则X服从

A．N(1,9)

B．N(1,2)

C．N(2,9)

D．N(1,4)

相似考题

1.设x1,x2,x3,…,x25是从均匀分布U(0,5)中抽取的一个样本,则样本均值近似服从的分布为________。A．N(5,1/2)B．N(5,1/10)C．N(2.5,1/12)D．N(2.5,1/10)

2.设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()

3.X服从标准正态分布(0,1),则Y=1＋2X的分布是:()A、N(1,2);B、N(1,4)C、N(2,4);D、N(2,5)。

4.两独立随机变量X和Y都服从正态分布,且X~N(3,4),Y~N(2,9)求D(X＋Y)=()。

更多“设（X, Y)~N（1,2;4,9;0.2)，则X服从A．N(1,9)B．N(1,2)C．N(2,9)D．N(1,4)”相关问题

  • 第1题：

    一个物理ID是由( )和( )来唯一定义。

    A.N^(1)

    B.N^(2)

    C.N^(3)

    D.N^(4)


    答案：AB

  • 第2题：

    假设X～N(-1,2),Y～N(1,3)，且X与Y相互独立，则X+2Y～

    A、N(1,8)

    B、N(1,14)

    C、N(1,40)

    D、N(1,22)


    正确答案:B

  • 第3题：

    设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。

    A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布

    B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布

    C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布

    D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布


    正确答案：D
    解析：中心极限定理指出，无论共同的分布是什么，只要随机变量的个数n相当大时，的分布总近似于正态分布。

  • 第4题：

    设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,


    答案：
    解析：
    【解】因为X，Y相互独立且都服从正态分布，所以X，Y的线性组合仍服从正态分布，即2=2X-Y+3服从正态分布，由E(Z)=2E(X)-E(Y)+3=5，D(Z)=4D(X)+D(Y)=9，则Z的密度函数为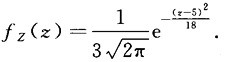

  • 第5题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第6题：

    若集合M={（x，y）｜ 3x一2y=-1），N={（x，y）｜ 2x+3y=8}，则M∩N=（）

    A.（1，2）
    B.{1，2}
    C.{（1，2）}
    D.φ

    答案：C
    解析：

  • 第7题：

    设n、m为一棵二叉树上的两个结点，在中序遍历时，n在m前的条件是()。

    A.n在m右方
    B.n是m祖先
    C.n在m左方
    D.n是m子孙

    答案：C
    解析：
    中序遍历时，先访问左子树，再访问根结点。n在m前，则n必须在m的左子树中。

  • 第8题：

    已知随机变量X服从正态分布N(μ，σ2)，设随机变量V=2X-3，则Y服从的分布是()。


    A.N(2μ-3，2σ2-3)

    B.N(2μ-3，4σ2-2)

    C.N(2μ-3，4σ2+9)

    D.N(2μ-3，4σ2-9)

    答案：B
    解析：
    由于随机变量X服从正态分布N(μ，σ2)，则随机变量y=2x-3的均值为2μ-3，方差为4σ2，故Y服从的分布是N(2μ-3，4σ2)。@##

  • 第9题：

    若随机变量X与Y相互独立，且X服从N（1，9），Y服从N（2，6），则X+Y服从（）分布。


    正确答案:N（3，25）

  • 第10题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第11题：

    对于两个独立的随机变量X，Y服从正态分布，即X~N（4，9），Y~N（1，4）则，E（2X+3Y）=（）。

    • A、9
    • B、11
    • C、13
    • D、7

    正确答案:B

  • 第12题：

    设随机变量X服从N（-1，4），则P｛X+1＜0｝=（）


    正确答案:0.5

  • 第13题：

    亚油酸是（ ）。

    A.n—3系脂肪酸

    B.n—6系脂肪酸

    C.n—7脂肪酸

    D.n—9系脂肪酸


    正确答案：B
    B

  • 第14题：

    具有n(n＞0)个顶点的无向图最多含有(37)条边。

    A．n(n-1)

    B．n(n+1)

    C．n(n-1)

    D．n(n+1)


    正确答案：C

  • 第15题：

    设Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，为样本均值，则的分布可以表示为( )。

    A．N(0，1/2)

    B．N(0，4)

    C．N(0，1/4)

    D．概率密度为

    E．N(0，1/8)


    正确答案：CD
    解析：因Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，所以其均值也服从正态分布，且均值为0，标准差为；将μ=0，σ=1/2代入正态分布的概率密度函数p(x)=，-∞x∞，可得的概率密度为。

  • 第16题：

    设随机变量X在［-1,2］上服从均匀分布,随机变量=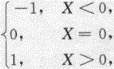则D(Y)=_______.


    答案：
    解析：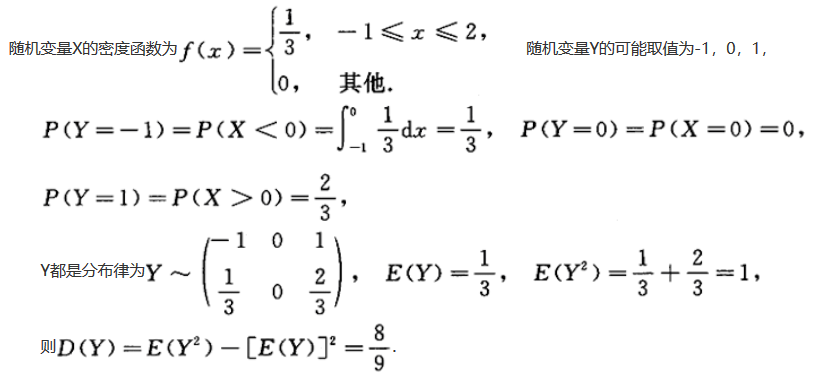

  • 第17题：

    设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
    　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).


    答案：
    解析：

  • 第18题：

    设随机变量X服从正态分布N(-1，9)，则随机变量Y=2-X服从( ).

    A.正态分布N(3，9)
    B.均匀分布
    C.正态分布N(1，9)
    D.指数分布

    答案：A
    解析：

  • 第19题：

    已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。


    A.N(2μ，2σ2)

    B.N(4μ，4σ2)

    C.N(2μ，4σ2)

    D.N(μ，σ2)

    答案：C
    解析：
    由于随机变量X服从正态分布N(μ，σ2)，则随机变量Y=2X的均值为2μ，方差为4σ2，即Y服从的分布是N(2μ，4σ2)。

  • 第20题：

    设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。


    答案：
    解析：
    解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

  • 第21题：

    若随机变量X～N（1，4），Y～N（2，9），且X与Y相互独立。设Z＝X－Y＋3，则Z～（）。


    正确答案:N（2，13）

  • 第22题：

    设X为服从正态分布N（-1，2）的随机变量，则E（2X-1）=（）。

    • A、9
    • B、6
    • C、4
    • D、-3

    正确答案:D

  • 第23题：

    设随机变量X服从正态分布N（-1，9），则随机变量Y=2-X服从（）．

    • A、正态分布N（3，9）
    • B、均匀分布
    • C、正态分布N（1，9）
    • D、指数分布

    正确答案:A

  • 第24题：

    对于两个独立的随机变量X，Y服从正态分布，即X~N（4，9），Y~N（1，4），则Z=X+Y服从（）分布。

    • A、Z~N（4，9）
    • B、Z~N（3，5）
    • C、Z~N（5，13）
    • D、Z~N（5，5）

    正确答案:C

相关内容