4个人玩游戏,在每张纸上写上l~9中的一个数字,然后叠起来,每人从中抽取2张,然后报出两数的关系,由此猜出剩下没有人拿的那个数字是多少。 已知:I.A说他手里的两数相加为lO。Ⅱ.B说他手里的两数相减为l。Ⅲ.C说他手里的两数之积为24。Ⅳ.D说他手里的两数之商为3。由此他们4人都猜出了剩下没有人拿的那个数字,这个数字是( )。 A. 5 B. 6 C. 7 D. 8
题目
B. 6
C. 7
D. 8
相似考题
参考答案和解析
更多“4个人玩游戏,在每张纸上写上l~9中的一个数字,然后叠起来,每人从中抽取2张,然后报出两数的关系,由此猜出剩下没有人拿的那个数字是多少。 已知:I.A说他手里的两数相加为lO。Ⅱ.B说他手里的两数相减为l。Ⅲ.C说他手里的两数之积为24。Ⅳ.D说他手里的两数之商为3。由此他们4人都猜出了剩下没有人拿的那个数字,这个数字是( )。 ”相关问题
-
第1题:
:一个两位数,十位上的数字是个位上的数字的丁2,把十位上与个位上的数字调换后,新数比原数大18,则原来这个两位数的两个数字和是( )
A.12
B.10
C.8
D.21
正确答案:B满足十位数是个位数字的导的数只能是23,46和69,这三个两位数的两个数字之和分别是5,10和15,选项中只出现10,所以选择B。
-
第2题:
第五题. 推理游戏
教授选出两个从2到9的数,把它们的和告诉学生甲,把它们的积告诉学生乙,让他们轮流猜这两个数
甲说:“我猜不出”
乙说:“我猜不出”
甲说:“我猜到了”
乙说:“我也猜到了”
问这两个数是多少
正确答案:第五题:3和4(可严格证明)
设两个数为n1,n2,n1>=n2,甲听到的数为n=n1+n2,乙听到的数为m=n1*n2
证明n1=3,n2=4是唯一解
证明:要证以上命题为真,不妨先证n=7
1)必要性:
i) n>5 是显然的,因为n<4不可能,n=4或者n=5甲都不可能回答不知道
ii) n>6 因为如果n=6的话,那么甲虽然不知道(不确定2+4还是3+3)但是无论是2,4还是3,3乙都不可能说不知道(m=8或者m=9的话乙说不知道是没有道理的)
iii) n<8 因为如果n>=8的话,就可以将n分解成 n=4+x 和 n=6+(x-2),那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10,那样n又可以分解成8+2,所以总之当n>=8时,n至少可以分解成两种不同的合数之和,这样乙说不知道的时候,甲就没有理由马上说知道。
以上证明了必要性
2)充分性
当n=7时,n可以分解成2+5或3+4
显然2+5不符合题
第五题:3和4(可严格证明)
设两个数为n1,n2,n1>=n2,甲听到的数为n=n1+n2,乙听到的数为m=n1*n2
证明n1=3,n2=4是唯一解
证明:要证以上命题为真,不妨先证n=7
1)必要性:
i) n>5 是显然的,因为n<4不可能,n=4或者n=5甲都不可能回答不知道
ii) n>6 因为如果n=6的话,那么甲虽然不知道(不确定2+4还是3+3)但是无论是2,4还是3,3乙都不可能说不知道(m=8或者m=9的话乙说不知道是没有道理的)
iii) n<8 因为如果n>=8的话,就可以将n分解成 n=4+x 和 n=6+(x-2),那么m可以是4x也可以是6(x-2)而4x=6(x-2)的必要条件是x=6即n=10,那样n又可以分解成8+2,所以总之当n>=8时,n至少可以分解成两种不同的合数之和,这样乙说不知道的时候,甲就没有理由马上说知道。
以上证明了必要性
2)充分性
当n=7时,n可以分解成2+5或3+4
显然2+5不符合题意,舍去,容易判断出3+4符合题意,m=12,证毕
于是得到n=7 m=12 n1=3 n2=4是唯一解。
意,舍去,容易判断出3+4符合题意,m=12,证毕
于是得到n=7 m=12 n1=3 n2=4是唯一解。
-
第3题:
宫浩的工牌号是一个五位数,它是由五个不同的数字构成,小周说:“它是85291。”小辛说:“它是16549。”小郭说:“它是59210。”小曾说:“每人都猜对了位置不相邻的两个数字。”宫浩的工牌号是多少?( )
A.86240
B.86149
C.51260
D.46280
正确答案:A
因为每人猜对两个数字,三人共猜对2×3=6(个)数字,而工牌号是五位数,所以必须有一位数字被两个人同时猜对,猜对的是左起第三位数字2。因为每人猜对的两个数字不相邻,所以周、郭猜对的另一个数字分别在两端,从而小辛猜对的数字是6和4,进一步推知小周猜对8,小郭猜对0。所以工牌号是86240。 -
第4题:
一个两位数,十位上的数字是个位上的数字的2/3,把十位上与个位上的数字调换后,新数比原数大
18,则原来这个两位数的两个数字之和是( )。
A.12
B.10
C.8
D.2l
正确答案:B
-
第5题:
一个两位数,十位数上的数字是个位上上数字的2/3,把十位与个位上的数调换后,新数比原数大18则原来两位数字的和是()
A.12
B.10
C.8
D.21
正确答案:B
-
第6题:
—个四位数,其个位上的数是其十位上的数的3倍,它后两位数字组成的两位数是其前 两位数字组成的两位数的3倍,求这个四位数各位数字之和是多少?A.16
B.18
C.19
D.21答案:A解析:
-
第7题:
10张卡片上分别写着从1到10的自然数,小王和小张分别从中抽出两张卡,并计算其中较大数字除以较小数字的结果,小王先抽,他抽到的卡片是3和9,小张在剩下卡片中抽取,计算出的结果比小王计算的结果大的概率:A.小于20%
B.在20%到30%之间
C.在30%到40%之间
D.大于40%答案:C解析:第一步,本题考查概率问题,属于分类分步型,用枚举法解题。
第二步,小王抽到的卡片是3和9,其计算结果为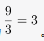
小张从剩下的1、2、4、5、6、7、8、10中任意抽取2张卡片,其结果比3大,假设小张抽取的较大数字的卡片情况如下:
抽到10,则第二张卡片可以是1、2,共2种;
抽到8,则第二张卡片可以是1、2,共2种;
抽到7,则第二张卡片可以是1、2,共2种;
抽到6、5或4,则第二张卡片都只能是1。共3种;
第三步,小张计算的结果比小王计算的结果大的情况数为2+2+2+3=9(种);总情况数为从剩下的8个数中抽取2个,有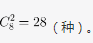
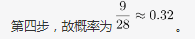
-
第8题:
4个人玩游戏,在每张纸上写上1~9中的一个数字,然后叠起来,每人从中抽取2张,然后报出两数的关系,由此猜出剩下没有人拿到的那个数字是多少。已知:
I.A说他手里的两数相加为10II. B说他手里的两数相减为1
III.C说他手里的两数之积为24
IV.D说他手里的两数之商为3
由此他们4人都猜出了剩下没有人拿的那个数字,这个数字是()
A.5
B.6
C. 7
D.8答案:C解析:本题为寻找假设型。本题题干中的前提不足够充分,要开展必要的假设去补充前提,从而合乎逻辑,推出结论。C可能拿3,8或4,6,D可能拿2,6或3,9或1,3。现分别假设:(1)假设C拿了3,8,则D只能拿2,6,进一步假设:如果A拿7,但3已经在C手中,I不成立;如果7,但6已经在D手中,8在C手中,II也不成立。结论是7不能有人拿。(2)假设C拿4,6,则D只能拿1,3或3,9,进一步假设:如果A拿7,但3已在D手中,I不成立,如果7,但6在C手中,B只能是7,8的组合可以成立II。此时,1,3,4,6,7,8或3,4,6,7,8,9被拿,剩余2,5,9或1,2,5,任意两项相加都不可能等于10,I不成立。结论还是7不可能有人拿。可知选C项。 -
第9题:
一个两位数,十位上的数字是个位上的数字的2/3,把十位上与个位上的数字调换后,新数比原数大18,则原来这个两位数的两个数字之和是( )。A. 12
B. 10
C. 8
D. 2l答案:B解析:故答案为B。 -
第10题:
小胡和小涂计算甲、乙两个两位数的乘积,小胡看错了甲数的个位数字,计算结果为1274;小涂看错了甲数的十位数字,计算结果为819。甲数是多少?
正确答案: 解:由于小胡和小涂都没有看错乙数,所以,乙数是1274和819的公约数。
1274=2×7×7×13
819=3×3×7×13
1274与819的公约数有1,7,13,91这四个。但是由“乙数是两位数”,可排除1和7;又由“小涂看错了的甲数也是两位数”,可排除91(不然的话,小涂看错了的甲数只能是一位数9)。因此,乙数必定是13。
根据乙数是13,可知小胡看错了的甲数是
1274÷13=98(8是看错的)
小涂看错了的甲数是
819÷13=63(6是看错的)
因此,甲数是93。
答案是93。 -
第11题:
在一张纸条上,老师写了甲乙丙丁等四个人中的一个人的名字,然后握在手里,让这四个人猜一猜是谁的名字。甲说:是丙的名字。乙说:不是我的名字。丙说:不是我的名字。丁说:是甲的名字。老师听完后说:”只有一个人说对了。请再猜一遍。”这四个人很快猜出了这张纸条上写的是谁的名字。问:这张纸条上究竟写的是谁的名字?
正确答案: 根据前提条件,第一次猜的结果,四个人中只有一个人的话说对了。其中甲的命题和丙的命题是矛盾的。根据矛盾律的要求,不可能都是真的,其中必然有一真,有一假。这样,其余两个人的话就必假。这样,乙的命题就与事实相反,所以纸条上就一定写的是乙的名字。 -
第12题:
问答题小胡和小涂计算甲、乙两个两位数的乘积,小胡看错了甲数的个位数字,计算结果为1274;小涂看错了甲数的十位数字,计算结果为819。甲数是多少?正确答案: 解:由于小胡和小涂都没有看错乙数,所以,乙数是1274和819的公约数。
1274=2×7×7×13
819=3×3×7×13
1274与819的公约数有1,7,13,91这四个。但是由“乙数是两位数”,可排除1和7;又由“小涂看错了的甲数也是两位数”,可排除91(不然的话,小涂看错了的甲数只能是一位数9)。因此,乙数必定是13。
根据乙数是13,可知小胡看错了的甲数是
1274÷13=98(8是看错的)
小涂看错了的甲数是
819÷13=63(6是看错的)
因此,甲数是93。
答案是93。解析: 暂无解析 -
第13题:
有一个四位数,把它从中间分成两半,得到前、后两个两位数,将前面的两位数的末尾添一个
零,然后加上前后两个两位数的乘积,恰好等于原来的四位数,又知道原数的个位数字为5,这个四位数是( )。
A.1985
B.1795
C.1895
D.1995
正确答案:D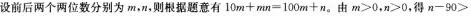
-
第14题:
一个四位数,其个位上的数是其十位上的数的3倍,它后两位数字组成的两位数是其前 两位数字组成的两位数的3倍,求这个四位数各位数字之和是多少?
A.16
B.18
C.19
D.21
正确答案:A
解析:个位上的数是其十位上的数的3倍的数的后两位只能是l3、26、39三种情况。又因为它后两位数组成的两位数是其前两位数组成的两位数的3倍,符合条件的只有39,那么这个四位数就为l339。它各位数字之和为1+3+3+9=16,答案选A。 -
第15题:
有一个四位数,把它从申间分成两半,得到前、后两个两位数,将前面的两位数的末尾添一个零,然后加上前后两个两位数的乘积,恰好等于原来的四位数,又知道原数的个位数字为5,这个四位数是( )。
A.1985
B.1795
C.1895
D.1995
正确答案:D
此题采用代入法,A项中190+19×85=1805≠1985,B项中170+17×95:1785≠1975,C项中180+18×95=1890~1895,D项190+19×95=1995,故选D。 -
第16题:
一个两位数,将个位数字与十位数字调换后,比原数小18,且这个原数是8的倍数,则这个数是多少?( )
A.24
B.32
C.40
D.64
正确答案:D
-
第17题:
10张卡片上分别写着从1到10的自然数,小王和小张分别从中抽出两张卡,并计算其中较大数字除以较小数字的结果,小王先抽,他抽到的卡片是3和9,小张在剩下卡片中抽取,计算出的结果比小王计算的结果大的概率:
A小于20%
B在30%到40%之间
C在20%到30%之间
D大于40%答案:B解析:解析:
故正确答案为B。 -
第18题:
已知一个四位数能够被15整除,其中百位数字比十位数字大2。如果将前两位数字与 后两位数字对调,得到的新数比原数的3倍大252,则原来的四位数是多少?
A.1755
B. 1530
C.3465
D.2532答案:A解析:此题用排除法。巳知该四位数能够被15整除,即能同时被3和5整除。若要被5整除, 个位数字必须为O或5,排除D项;根据题干要求,百位数字比十位数字大2,排除C项;将四位数的前两位数字 与后两位对调,得到的新数比原数的3倍大252,只有A项符合,5517=1755x3+252。 -
第19题:
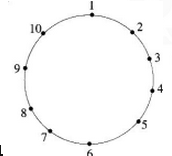
十个人围成一个圆圈,每人选择一个整数并告诉他的两个邻座的人,然后每人算出并宣布他两个邻座所选数的平均数,这些平均数如右图所示,则宣布6的那个人选择的数是多少?
 A.l
A.l
B.2
C.3
D.4答案:B解析:设宣布1~10的人选择的数分别是,a1,a2,a3,,…am。由图形可知a2+a4=3×2=6,a4+a6=5×2=10,a6+a8=7×2=14,a6+a8=9×2=18,a10+a2=1×2=2,等式左右分别相加,得到2(a2+a4+a6+a8+a10)=6+10+14+18+2=50,则(a2+a4)+a4+(a8+a10)=25,所以a6=25-6-18=1,应选择A。 -
第20题:
4个人玩游戏,在每张纸上写上1?9中的一个数字,然后叠起来,每人从中抽取2张,然后报出两数的关系,由此猜出剩下没有人拿到的那个数字是多少。已知:
I . A说他手里的两数相加为10
II. B说他手里的两数相减为1
III. C说他手里的两数之积为24
IV. D说他手里的两数之商为3
由此他们4人都猜出了剩下没有人拿的那个数字,这个数字是( )
A. 5 B. 6
C. 7 D.8答案:C解析:本题为寻找假设型。本题题干中的前提不足够充分,要开展必要的假设去补充前提,从而合乎逻辑,推出结论。C可能拿3,8或4,6,D可能拿2,6或3,9或1,3。现分别假设: (1)假设C拿3,8,则D只能拿2,6,进一步假设:如果A拿7,但3已经在C手中,I不成立;如果 B拿7,但6已经在D手中,8在C手中,II也不成立。结论是7不能有人拿。(2)假设C拿4,6,则 D只能拿1,3或3,9,进一步假设:如果A拿7,但3已在D手中,I不成立;如果B拿7,但6在C 手中,B只能是7,8的组合可以成立II。此时,1,3,4,6,7,8或3,4,6,7,8,9被拿,剩余2,5,9或 1,2,5,任意两项相加都不可能等于10,I不成立。结论还是7不可能有人拿。可知选C项。 -
第21题:
在数的运算中,一般地说,两数相加或相减,应该使它们具有相同精确度;两数相乘或相除,应使它们有相同的准确度,即每一个数都保留同样位数的有效数字,计算结果也是如此。()
正确答案:正确 -
第22题:
在两个近似数相乘或相除时,有效数字较多的近似数,只须比有效数字少的那个多保留()位。
- A、1
- B、2
- C、3
- D、4
正确答案:A -
第23题:
判断题在数的运算中,一般地说,两数相加或相减,应该使它们具有相同精确度;两数相乘或相除,应使它们有相同的准确度,即每一个数都保留同样位数的有效数字,计算结果也是如此。()A对
B错
正确答案: 对解析: 暂无解析
