（本题满分8分）甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由．

题目

（本题满分8分）

甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由．

相似考题

1.与同伴做下面的游戏：每个人从一副扑克牌（去掉大、小王和J，Q，K）中选择3张黑色牌和3张红色牌（黑色牌代表正分，红色牌代表负分），使得6张牌的总分为零。两人轮流从同伴手中抽1张牌，10次以后，计算每人手中牌的总分，得分高者获胜。

2.一个两位数，十位数字是个位数字的2倍，将两个数字对调后得到的两位数比原来的数小36，求这个两位数。

3.（本题满分6分）小莉的爸爸买了今年七月份去上海看世博会的一张门票，她和哥哥两人都很想去观看，可门票只有一张，读九年级的哥哥想了一个办法，拿了八张扑克牌，将数字为1，2，3，5的四张牌给小莉，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小莉和哥哥从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则小莉去；如果和为奇数，则哥哥去．（1）请用数状图或列表的方法求小莉去上海看世博会的概率；

4.从一副混合后的扑克牌（52张）中随机抽取2张，则“抽出的2张均为红桃”的概率为_________（结果用最简分数表示）。

参考答案和解析
正确答案：

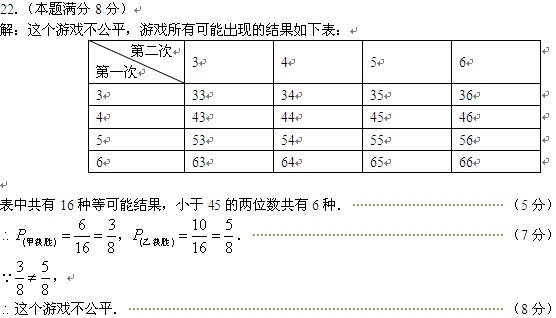
更多“（本题满分8分）甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏．游戏规则是：将这4张牌的正面全部朝下，洗匀，从中随机抽取一张，抽得的数作为十位上的数字，然后，将所抽的牌放回，正面全部朝下、洗匀，再从中随机抽取一张，抽得的数作为个位上的数字，这样就得到一个两位数．若这个两位数小于45，则甲获胜，否则乙获胜．你认为这个游戏公平吗？请运用概率知识说明理由．”相关问题

  • 第1题：

    ：一个两位数，十位上的数字是个位上的数字的丁2，把十位上与个位上的数字调换后，新数比原数大18，则原来这个两位数的两个数字和是（ ）

    A．12

    B．10

    C．8

    D．21


    正确答案：B

    满足十位数是个位数字的导的数只能是23，46和69，这三个两位数的两个数字之和分别是5，10和15，选项中只出现10，所以选择B。

  • 第2题：

    甲、乙两人分别从随机数字表抽得30个（各取两位数字）随机数字作为两个样本，求得则理论上

    A、

    B、作两样本t检验，必然得出无差别的结论

    C、作两方差齐性的F检验，必然方差齐

    D、分别由甲、乙两样本求出的总体均数的95%可信区间，很可能有重叠

    E、分别由甲、乙两样本求出的总体均数的95%可信区间，一定不重叠


    参考答案：D

  • 第3题：

    ● 甲和乙用如下图的两个转盘做游戏，游戏规则如下：分别旋转两个转盘，当两个转盘所转到的数字之积为奇数时，甲得 2 分；当所转到的数字之积为偶数时，乙得1分，则这游戏规则 （16） 。

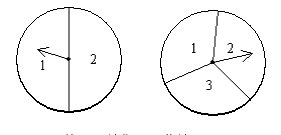
    （16）

    A. 对双方都公平

    B. 对甲不公平

    C. 对乙不公平

    D. 对双方都不公平


    正确答案：A

  • 第4题：

    有一个两位数，如果用它去除以个位数字，商为9余数为6，如果用这个两位数除以个位数字与十位数字之和，则商为5余数为3。这个两位数为（ ）。 A．33 B．78 C．38或78 D．33或78


    正确答案：D
    设这个两位数为10a+b，则有10a+6＝96+6，1Oa+b=5(a+b)+3，两式化简得到相同的方程5a－4b=3，将各选项代入，可知33、78均满足。故选D。

  • 第5题：

    ：一个两位数，将个位数字与十位数字调换后，比原数小18，且这个原数是8的倍数，则这个数是多少?（ ）

    A．24

    B．32

    C．40

    D．64


    正确答案：D

  • 第6题：

    —个四位数，其个位上的数是其十位上的数的3倍，它后两位数字组成的两位数是其前 两位数字组成的两位数的3倍，求这个四位数各位数字之和是多少？

    A.16
    B.18
    C.19
    D.21

    答案：A
    解析：

  • 第7题：

    在一场“请问谁在说谎”的游戏中，四位游戏参与者每人从一副没有大小王的扑克牌中抽取一张。
    甲说：“我抽中的牌是黑桃。”
    乙说：“我抽中的牌是红桃。”
    丙说：“我抽中的牌不是红桃。”
    丁说：“我抽中的牌是梅花。”
    已知4人抽取的扑克牌花色各不相同，且只有一人说谎。
    根据上述条件，下列说法正确的是：

    A.甲、乙、丙、丁四人均有可能说谎
    B.可以推知每个人抽取的扑克牌花色
    C.丙有可能抽中方块
    D.乙抽中的牌一定是红桃

    答案：D
    解析：
    第一步，确定题型。
    题干有若干论断和真假限定，确定为真假推理。
    第二步，分析条件，进行推理。
    题干无矛盾或反对关系，可考虑使用假设法，乙与丙均提到了红桃，可对乙或丙进行假设。
    假设乙说谎，则其他几人说真话。乙说谎，则乙抽中的不是红桃；其余为真，则甲、丙、丁抽中的牌都不是红桃。此时，没有人抽中红桃，与题干矛盾，该假设不成立。
    故乙说的肯定为真话，即乙抽中的是红桃。
    因此，选择D选项。

  • 第8题：

    甲从1、2、3中抽取一个数，记为a；乙从1、2、3、4中抽取一个数，记为b，规定当a大于b或者a+1小于b时甲获胜，则甲取胜的概率为（ ）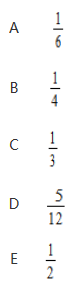


    答案：E
    解析：
    穷举法：满足a大于b的有（2,1）（3,1）（3,2）；满足a+1小于b的有（1,3）（1,4）（2,4）；共六组，因此概率为3/6=1/2

  • 第9题：

    一个两位数，十位上的数字是个位上的数字的2／3，把十位上与个位上的数字调换后，新数比原数大18，则原来这个两位数的两个数字之和是( )。

    A. 12
    B. 10
    C. 8
    D. 2l

    答案：B
    解析：
    故答案为B。

  • 第10题：

    你正在玩扑克牌游戏，从52张牌中抽出两张。如果你抽到的第一张牌是A，第二张牌是K，你就赢了。你赢得游戏的概率是多少？（）

    • A、（4/52）x（4/51）
    • B、2/52
    • C、（4/52）x（4/52）
    • D、（1/4）x（1/4）

    正确答案:A

  • 第11题：

    在一副52张的扑克牌中（没有大小王）任意抽取一张牌，抽出的这张牌是方块的机会是（）。

    • A、1/2
    • B、1/4
    • C、1/3
    • D、0

    正确答案:B

  • 第12题：

    单选题
    在一副扑克牌中单独抽取一次，抽到一张红桃或爱司的概率是（）
    A

    1/4

    B

    1/52

    C

    1/8

    D

    1/2


    正确答案： A
    解析： 暂无解析

  • 第13题：

    有一个四位数，把它从中间分成两半，得到前、后两个两位数，将前面的两位数的末尾添一个

    零，然后加上前后两个两位数的乘积，恰好等于原来的四位数，又知道原数的个位数字为5，这个四位数是（ ）。

    A．1985

    B．1795

    C．1895

    D．1995


    正确答案：D

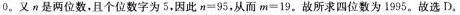
  • 第14题：

    有一个两位数，它的十位数字比个位数字大1，并且这个两位数大于30且小于42，求这个两位数。

  • 第15题：

    一个两位数，十位上的数字是个位上的数字的2／3，把十位上与个位上的数字调换后，新数比原数大

    18，则原来这个两位数的两个数字之和是( )。

    A．12

    B．10

    C．8

    D．2l


    正确答案：B

  • 第16题：

    一个两位数，十位数上的数字是个位上上数字的2/3，把十位与个位上的数调换后，新数比原数大18则原来两位数字的和是（）

    A.12

    B.10

    C.8

    D.21


    正确答案：B

  • 第17题：

    在一副52张扑克牌中(没有大小王)任意抽取一张牌，抽出的这张牌是方块的机会是
    （　　）．

    A.1／2
    B.1／4
    C.1／3
    D.0

    答案：B
    解析：
    52张牌中，每种图形的牌数都是13张，所以，抽取方块的机会是13／52=1／4.

  • 第18题：

    一个四位数，其个位上的数是其十位上的数的3倍，它后两位数字组成的两位数是其前两位数字组成的两位数的3倍，求这个四位数各位数字之和是多少？

    A.16
    B.18
    C.19
    D.21

    答案：A
    解析：
    个位上的数是其十位上的数的3倍的数的后两位只能是13、26、39三种情况。又因为 它后两位数组成的两位数是其前两位数组成的两位数的3倍，符合条件的只有39，那么这个四位数就为1339， 它各位数字之和为1+3+3+9=16，答案选A。

  • 第19题：

    在分别记了数字1、2、3、4、5、6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为（ ）



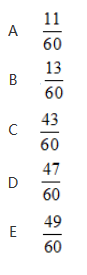    答案：D
    解析：

  • 第20题：

    有三张扑克牌，牌的数字互不相同，并且都在10以内。把三张牌洗好后，分别发给甲、乙、丙每人一张。每人记下自己牌的数字，再重新洗牌、发牌、记数。这样反复几次后，三人各自记录的数字之和分别为17、18、22。这三张牌的数字之和是多少？（ ）

    A.15
    B.17
    C.18
    D.19

    答案：D
    解析：
    本题属于倍数特性。
    每一轮发牌，三张牌的总和是一样的，设为s，几轮下来三人的数字之和应为s的倍数，即17＋18＋22＝57＝ns，四个选项只有19能被57整除。

  • 第21题：

    一副卡牌上面写着1到10的数字，甲和乙从中分别随机抽取三张牌，并比较其中较大的两张牌的牌面之积，数字大的人获胜。甲先抽出三张牌，上面的数字分别是2、6和8，问乙从剩下的牌中抽取三张牌的话，其胜过甲的概率（ ）

    A. 高于60%
    B. 在50%60%之间
    C. 在40%50%之间
    D. 低于40%

    答案：C
    解析：
    本题属于概率问题，选择C项。甲的最大乘积为6*8=48，要求乙胜过甲的话，其乘积大于48即可，由此，（1-10中除了2、6、8）可以是
    （1）5、10 （第三个数可以为1、3、4）三种；
    （2）7、10 （第三个数可以为1、3、4、5）四种；
    （3）9、10 （第三个数可以为1、3、4、5、7）五种；
    （4）7、9 （第三个数可以为1、3、4、5）四种；共计16种.
    所以概率为，因此选择C项。

  • 第22题：

    在一副扑克牌中单独抽取一次，抽到一张红桃或爱司的概率是（）

    • A、1/4
    • B、1/52
    • C、1/8
    • D、1/2

    正确答案:A

  • 第23题：

    单选题
    你正在玩扑克牌游戏，从52张牌中抽出两张。如果你抽到的第一张牌是A，第二张牌是K，你就赢了。你赢得游戏的概率是多少？（）
    A

    （4/52）x（4/51）

    B

    2/52

    C

    （4/52）x（4/52）

    D

    （1/4）x（1/4）


    正确答案： A
    解析： 当抽第一张牌时，52张牌中有4张A。当抽第二张牌时，51张牌中有4个K。因此，赢得游戏的概率是（4/52）x（4/51）。

相关内容