数学奥林匹克高中训练题37
在高中数学中,算法应作为一种核心观念贯穿于高中数学教学的始终。()
此题为判断题(对，错)。
正确答案：√
《普通高中数学课程标准(实验)》的基本理念给高中数学课程的定位是基础性、普及性和发展性。()
此题为判断题(对，错)。
正确答案：×
高中数学《几何概型》
一、考题回顾
一、考题回顾
答案：
解析：
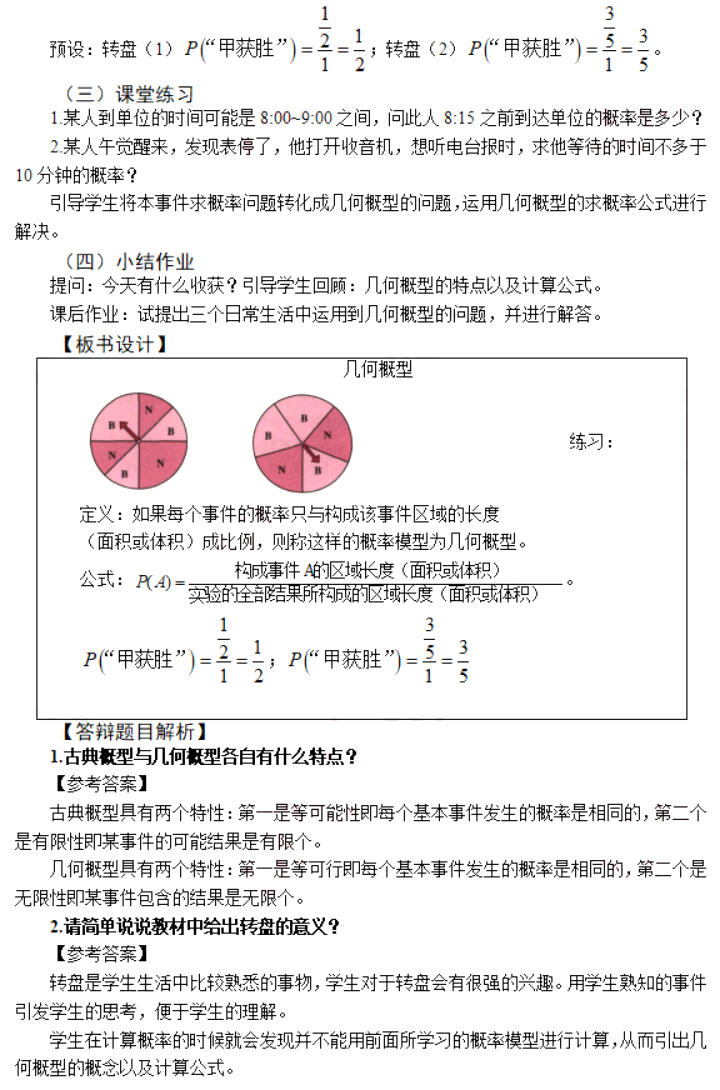
高中数学《余弦定理的证明》
一、考题回顾
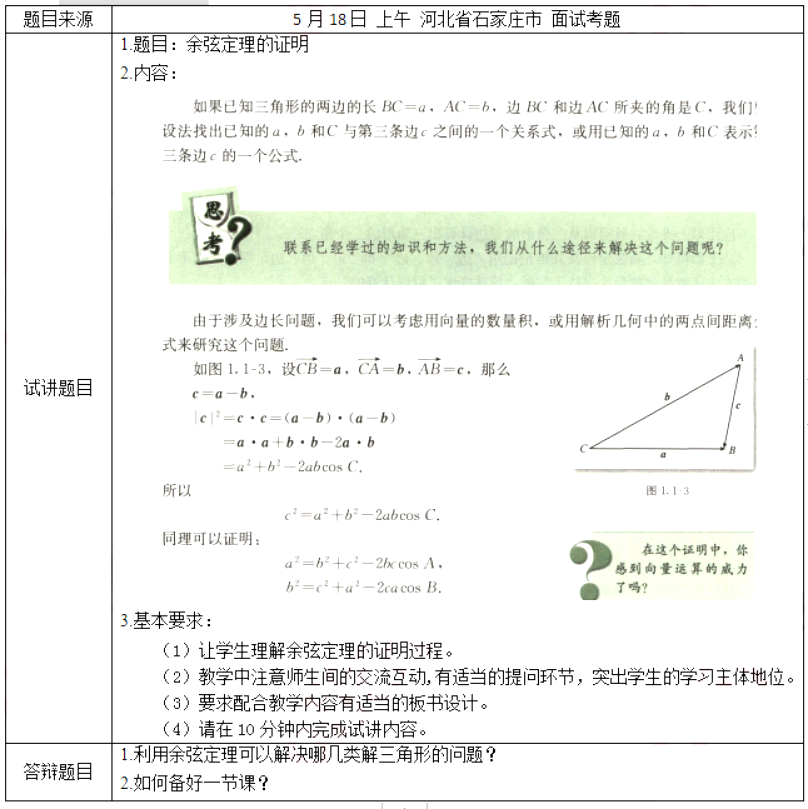
一、考题回顾
答案：
解析：
二、考题解析
【教学过程】
(一)导入新课
情景导入：多媒体展示修路工人开凿山地隧道的情境图。提问：“为了测量山地隧道的长度，工人先在山顶选一个位置A，量出A点到隧道两端的距离AB、AC及AB与AC的夹角，最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设：已知三角形两边及其夹角，去求另一边的数学问题。
提问：“那工人们是如何算出来的呢?”
引发认知冲入，从而引出课题。
(四)小结作业
小结：通过这节课的学习，你有什么收获?
作业：课后题。
【板书设计】
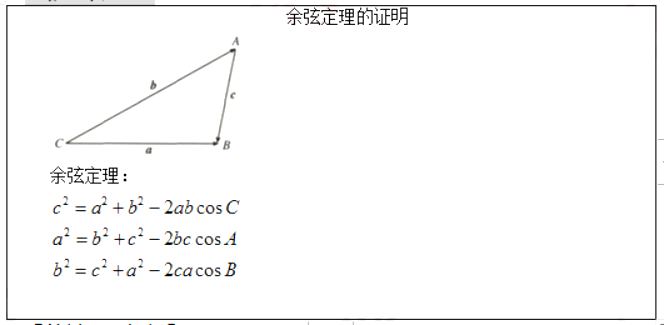
【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边，求三个角。
(2)已知两边和夹角，求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课，要从以下几个方面准备：
首先，备教材，教材分析是教师备好课、上好课的基本保证，对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提，更是教师进行教学研究的一种主要方法。
其次，备学生。教学的基本前提是为了学生而进行的教学，其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后，备教学方法。现代教学理论认为，在教学过程中，学生是学习的主体，教师是学习的组织者、引导者，教学的一切活动都必须以强调学生的主动性、积极性为出发点。
【教学过程】
(一)导入新课
情景导入：多媒体展示修路工人开凿山地隧道的情境图。提问：“为了测量山地隧道的长度，工人先在山顶选一个位置A，量出A点到隧道两端的距离AB、AC及AB与AC的夹角，最后算出隧道长度。哪位同学能说说这是一个什么数学问题?”
预设：已知三角形两边及其夹角，去求另一边的数学问题。
提问：“那工人们是如何算出来的呢?”
引发认知冲入，从而引出课题。
(四)小结作业
小结：通过这节课的学习，你有什么收获?
作业：课后题。
【板书设计】
【答辩题目解析】
1.利用余弦定理可以解决哪几类解三角形的问题?
【参考答案】
(1)已知三边，求三个角。
(2)已知两边和夹角，求第三边和其他两个角。
2.如何备好一节课?
【参考答案】
一节好的数学课，要从以下几个方面准备：
首先，备教材，教材分析是教师备好课、上好课的基本保证，对教师顺利完成教学任务、提升教学质量有十分重要的意义。分析教材的过程既是教学科学把握教学内容、加深对教育理论的重要前提，更是教师进行教学研究的一种主要方法。
其次，备学生。教学的基本前提是为了学生而进行的教学，其根本目的在于促进学生的主动发展。因此在备课时要充分考虑所面对的学生特点。
最后，备教学方法。现代教学理论认为，在教学过程中，学生是学习的主体，教师是学习的组织者、引导者，教学的一切活动都必须以强调学生的主动性、积极性为出发点。
高中数学《奇函数的性质》
一、考题回顾
一、考题回顾
答案：
解析：
二、考题解析
【教学过程】
(一)导入新课
回顾偶函数的定义及性质。
教师引导：偶函数是轴对称性质在函数图象中的一种特殊体现。除了轴对称，我们还学过什么样的对称性呢?
预设：还有中心对称。
引题：今天我们就来学习中心对称性质在函数图象中的一种特殊体现。
板书课题《奇函数的性质》。
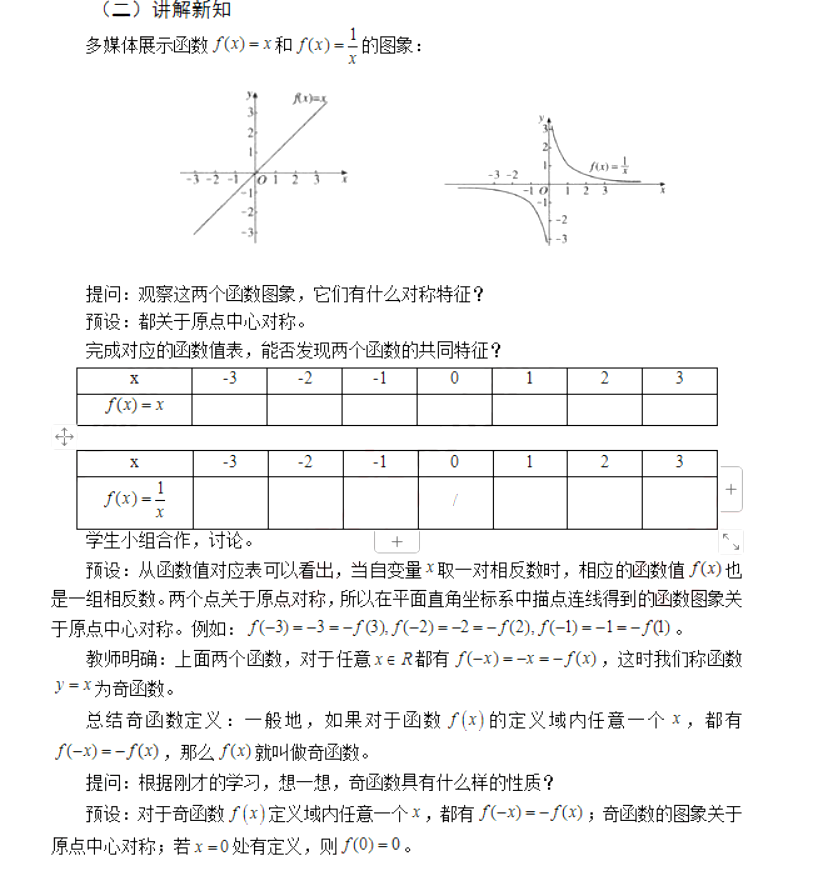
【参考答案】
知识与技能：理解并掌握奇函数的定义及其性质，会灵活运用奇函数的性质解决问题。
过程与方法：经历奇函数概念的形成过程，体会从特殊到一般的数学思想方法，提高分析问题、解决问题的能力。
情感态度与价值观：积极参与学习过程，激发学习兴趣，提高学习信心，培养良好的数学学习习惯。
【教学过程】
(一)导入新课
回顾偶函数的定义及性质。
教师引导：偶函数是轴对称性质在函数图象中的一种特殊体现。除了轴对称，我们还学过什么样的对称性呢?
预设：还有中心对称。
引题：今天我们就来学习中心对称性质在函数图象中的一种特殊体现。
板书课题《奇函数的性质》。
【参考答案】
知识与技能：理解并掌握奇函数的定义及其性质，会灵活运用奇函数的性质解决问题。
过程与方法：经历奇函数概念的形成过程，体会从特殊到一般的数学思想方法，提高分析问题、解决问题的能力。
情感态度与价值观：积极参与学习过程，激发学习兴趣，提高学习信心，培养良好的数学学习习惯。
奥林匹克高中训练题37,PDF,高中奥,训练题,pdf,数学奥林匹克,测试题,高中数学,高级中学,高中数学奥,奥林匹克,数学答案,练习题
高中数学《平面与平面的位置关系》
一、考题回顾
一、考题回顾
答案：
解析：
二、考题解析
【教学过程】
(一)导入新知
回顾直线与直线、直线与平面的位置关系。提问：平面与平面的位置关系又是如何的呢?
引出课题——平面与平面的位置关系。
(三)课堂练习
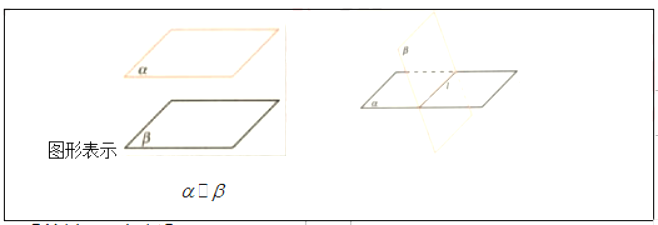
如果三个平面两两相交，那么它们的交线有多少条?画出图形表示你的结论。
(四)小结作业
提问：今天有什么收获?引导学生回顾平面与平面的位置关系。
课后作业：练习题目。
【板书设计】
【答辩题目解析】
1.本节课在教材中有着什么样的地位和作用?
【参考答案】
《平面与平面的位置关系》选自人教版高中数学必修二第二章第一节，本节课主要讲解的是平面与平面的相交和平行，在此之前，学生已经学习了《平面》，认识了平面，了解了一些相关的公理，本节课是对学生原有的平面知识的拓展，也为今后学习空间立体几何打下基础，有着承上启下的作用。
2.在本节课的教学过程中，对于探究平面与平面的位置关系你是如何设计的?
【参考答案】
首先，设置了两个活动，一个是让学生将两本书看做两个平面，在移动和翻转的过程中观察它们的位置关系有几种，另一个是观察出示的长方体，思考围成长方体的六个面两两之间的位置关系有几种。通过这两个活动，让学生结合实例思考平面与平面的位置关系有几种，最后师生共同总结出平面与平面的位置关系，并说明如何用图形表示平面与平面的位置关系。接着，让学生自己尝试用图形表示。最后设置小组讨论，根据平面与平面的位置关系探究直线与直线的位置关系。整个教学过程，采用学生观察，师生总结，最后设置问题，将知识形成体系的方式来探究平面与平面的位置关系。
【教学过程】
(一)导入新知
回顾直线与直线、直线与平面的位置关系。提问：平面与平面的位置关系又是如何的呢?
引出课题——平面与平面的位置关系。
(三)课堂练习
如果三个平面两两相交，那么它们的交线有多少条?画出图形表示你的结论。
(四)小结作业
提问：今天有什么收获?引导学生回顾平面与平面的位置关系。
课后作业：练习题目。
【板书设计】
【答辩题目解析】
1.本节课在教材中有着什么样的地位和作用?
【参考答案】
《平面与平面的位置关系》选自人教版高中数学必修二第二章第一节，本节课主要讲解的是平面与平面的相交和平行，在此之前，学生已经学习了《平面》，认识了平面，了解了一些相关的公理，本节课是对学生原有的平面知识的拓展，也为今后学习空间立体几何打下基础，有着承上启下的作用。
2.在本节课的教学过程中，对于探究平面与平面的位置关系你是如何设计的?
【参考答案】
首先，设置了两个活动，一个是让学生将两本书看做两个平面，在移动和翻转的过程中观察它们的位置关系有几种，另一个是观察出示的长方体，思考围成长方体的六个面两两之间的位置关系有几种。通过这两个活动，让学生结合实例思考平面与平面的位置关系有几种，最后师生共同总结出平面与平面的位置关系，并说明如何用图形表示平面与平面的位置关系。接着，让学生自己尝试用图形表示。最后设置小组讨论，根据平面与平面的位置关系探究直线与直线的位置关系。整个教学过程，采用学生观察，师生总结，最后设置问题，将知识形成体系的方式来探究平面与平面的位置关系。
高中数学《线面垂直的判定》
一、考题回顾
一、考题回顾
答案：
解析：
高中数学《圆的标准方程》
答案：
解析：
高中数学《曲线与方程》
答案：
解析：
高中数学《等比数列》
一、考题回顾
一、考题回顾
答案：
解析：
更多 “数学奥林匹克高中训练题37” 相关考题
考题
简述高中数学课程的地位和作用。 答案：解析：高中数学课程是义务教育后普通高级中学的一门主要课程，它包含了数学中最基本的内容。是培养公民素质的基础课程。高中数学课程对于认识数学与自然界、数学与人类社会的关系，认识数学的科学价值、文化价值，提高提出问题、分析和解决问题的能力，形成理性思维，发展智力和创新意识具有基础性的作用。
高中数学课程有助于学生认识数学的应用价值，增强应用意识，形成解决简单实际问题的能力。高中数学课程是学习高中物理、化学、技术等课程和进一步学习的基础。同时，它为学生的终身发展，形成科学的世界观、价值观奠定基础，对提高全民族素质具有重要意义。
考题
下列关于高中数学基础性的说法不正确的是（ ）A.高中数学课程为学生进一步学习提高了必要的数学准备
B.高中数学为不同学生提供相同的基础
C.高中数学课程体现时代性、基础性和选择性
D.高中数学课程要以学生的发展为本，尊重他们的个性发展答案：B解析：本题考查高中数学课程的性质选项A、C、D都体现了高中数学课程的定位，高中数学课程面向全体学生，为不同兴趣和志向、不同发展方向、进入不同高校不同专业学习的学生提供适合他们的数学基础，高中数学课程为不同学生提供不同的基础。
考题
单选题下列关于高中数学课程结构的说法不正确的是（）。A
高中数学课程可分为必修与选修两类B
高中数学选修课程包括4个系列的课程C
高中数学必修课程包括5个模块D
高中课程的组合具有固定性，不能发生改变正确答案：C解析：高中数学课程可分为必修与选修两类，必修课程由五个模块组成，选修课程包括四个系列。高中课程的组合具有一定的灵活性，不同的组合可以相互转换。学生在做出选择之后，可以根据自己的意愿和条件向学校提出申请调整，经过测试获得相应的学分即可转换。
考题
简述高中数学课程的地位和作用。答案：解析：本题主要考查对《高中数学新课程标准》的理解。高中数学课程对于认识数学与自然界、数学与人类社会的关系，认识数学的科学价值、文化价值，提高提出问题、分析和解决问题的能力，形成理性思维，发展智力和创新意识具有基础性的作用。高中数学课程有助于学生认识数学的应用价值，增强应用意识，形成解决简单实际问题的能力。高中数学课程是学习高中物理、化学、技术等课程和进一步学习的基础。同时，它为学生的终身发展，形成科学的世界观、价值观奠定基础，对提高全民族素质具有重要意义。
考题
简述高中数学课程的地位和作用。 答案：解析：高中数学课程是义务教育后普通高级中学的一门主要课程，它包含了数学中最基本的内容是培养公民素质的基础课程。
高中数学课程对于认识数学与自然界、数学与人类社会的关系，认识数学的科学价值、文化价值．提高提出问题、分析和解决问题的能力，形成理性思维，发展智力和创新意识具有基础性的作用。
高中数学课程有助于学生认识数学的应用价值，增强应用意识，形成解决简单实际问题的能力。
高中数学课程是学习高中物理、化学、技术等课程和进一步学习的基础。同时，它为学生的终身发展．形成科学的世界观、价值观奠定基础，对提高全民族素质具有重要意义。
考题
单选题下列关于高中数学基础性的说法不正确的是（）。A
高中数学课程为学生进一步学习提供了必要的数学准备B
高中数学课程为不同学生提供相同的基础C
高中数学课程体现时代性、基础性和选择性D
高中数学课程要以学生的发展为本，尊重他们的个性发展正确答案：D解析：选项A、C、D都体现了高中数学课程的定位，高中数学课程面向全体学生，为不同兴趣和志向、不同发展方向、进入不同高校不同专业学习的学生提供适合他们的数学基础，为不同的学生提供的基础是不同的，所以选项B是错误的。故选B。
考题
单选题下列关于高中数学基础性的说法不正确的是（）。A
高中数学课程为学生进一步学习提供了必要的数学准备B
高中数学课程为不同学生提供相同的基础C
高中数学课程体现时代性、基础性和选择性D
高中数学课程要以学生的发展为本，尊重他们的个性发展正确答案：C解析：选项A、C、D都体现了高中数学课程的定位，高中数学课程面向全体学生，为不同兴趣和志向、不同发展方向、进入不同高校不同专业学习的学生提供适合他们的数学基础，为不同的学生提供的基础是不同的，所以选项B是错误的。故选B。
考题
单选题高中数学要强调对数学的本质的认识，否则会将什么淹没在形式化海洋里：（）A
数学思维活动B
解题训练活动正确答案：A解析：暂无解析