南通棋牌游戏中心下载2010年全国各地数学中考试题

△ABC中,AB=13cm,BC=10cm,BC边上的中线AD=12cm.求AC
方法①∠B小于90°;
左上为A,左下为B,右下为C,右上为D;
已知∠B=∠D;AB=CD;
证明:过A作AN⊥BC于N;
过C作CM⊥AD于M;
连接AC
∵AN⊥BC;CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D;AB=CD
∴△ANB=△DMC(AAS)
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°,AC=AC
∴△ACD=△AMD(HL)
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
方法②∠B大于90°
左上为A,左下为B,右下为C,右上为D;
已知∠B=∠D;AB=CD;
证明:延长CD,过A作AN⊥BC于N;
延长AB,过C作CM⊥AD于M;
连接AC
∵AN⊥BC;CM⊥AD
∴∠ANB=∠DMC=90°
又∵∠B=∠D;AB=CD
∴△ANB=△DMC(AAS)
∴AN=CM;BN=DM
又∵∠ANB=∠DMC=90°,AC=AC
∴△ACD=△AMD(HL)
∴AM=DN
又∵BN=DM
∴BD=AC
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
方法③∠B等于90°
证明:∵∠B=∠D=90°;AB=CD;AC=AC
∴△ABC=△ADC(HL)
∴AB=CB
∵BD=AC;AB=CD
∴凸四边形ABCD为平行四边型。
有错吗?若我的证明有错请明示,我知道有个反例,但它是凹四边形。
在等腰三角形ABC中,A是顶角,且cosA=-21,则cosB=( )

A.A
B.B
C.C
D.D
本题主要考查的知识点为三角函数式的变换.【应试指导】
在△ABC中,D、E分别是边AB、AC的中点,若BC=5,则DE的长是( )。
A.2.5
B.5
C.10
D.15
分析:由D、E分别是边AB、AC的中点可知,DE是ABC的中位线,根据中位线定理可知,DE=BC=
 2.5。
2.5。涉及知识点:中位线
点评:本题考查了中位线的性质,三角形的中位线是指连接三角形两边中点的线段,中位线的特征是平行于第三边且等于第三边的一半。
推荐指数:★★
摘要:【官方直通车AG9858、COM】2010年全国各地数学中考试题分类汇编26三角形的基础知识一、选择题1.(2010江苏苏州)如图,在△ABC中,D、E两点分别在BC、AC边上.若BD=CD,∠B=∠CDE,DE=2,则AB的长度是A.4B.5C.6D.7【答案】A2.(2010安徽省中中考)如图,直线l1∥l2,∠1=550,∠2=650,则∠3为……………)……………(A)500.B)550C)600D)650【答案】C3.(2010广东广州,4,3分)在△ABC中,D、E分别是边AB、AC的中点,若BC=5,则DE的长是()A.2.5B.5C.10D.15【分析】由D、E分别是边AB、AC的中点可知,DE是△ABC的中位线,根据中位线定理可知,DE=1BC=2.5.2【答案】A【涉及知识点】中位线【点评】本题考查了中位线的性质,三角形的中位线是指连接三角形两边中点的线段,中位线的特征是平行于第三边且等于第三边的一半.4.(10湖南益阳)如图3,已知△ABC,求作一点P,使CPAB P到∠A的两边的距离相等,且PA=PB.下列确定P点的方法正确的是A.P为∠A、∠B两角平分线的交点B.P为∠A的角平分线与AB的垂直平分线的交点C.P为AC、AB两边上的高的交点图3D.P为AC、AB两边的垂直平分线的交点【答案】B5.(2010山东济宁)若一个三角形三个内角度数的比为2︰3︰4,那么这个三角形是A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形【答案】B6.(2010四川凉山)将一副三角板按图中的方式叠放,则角等于A.75oB.60oC.45o

(1)求证:BE是⊙0的切线;
(2)若BC=√3,AC=5,求圆的直径AD及切线BE的长。
∵AO=BO,∴∠BAD=∠ABO,
又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°,
∵B0是圆的半径,∴BE是⊙O的切线。
(2)设圆的半径为r,连接CD交OB于F,
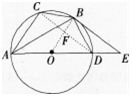
设圆的半径为R,连接CD,.




B.14
C.15
D.16


(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.




(1)当MN∥AC且BM=12.5时,求线段MN的长。
(2)当MN与AC不平行时,△CMN可能成为直角三角形吗?若可能,请写出线段CN长的取值范围;若不可能,请说明理由。


