如图5,在△ABC中,∠ABC=90o,∠CBD=40o,AC∥BD,则∠A=__________度。
题目
如图5,在△ABC中,∠ABC=90o,∠CBD=40o,AC∥BD,则∠A=__________度。

相似考题
更多“如图5,在△ABC中,∠ABC=90o,∠CBD=40o,AC∥BD,则∠A=__________度。”相关问题
-
第1题:
如图,D是△ABC内的一点,BD⊥CD,AD=6,BD=8,CD=6,E,F,G,H分别是AB,AC,CD, BD的中点.则四边形EFGH的周长是()。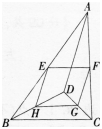 A.12
A.12
B.14
C.15
D.16答案:D解析:因为BD⊥CD,BD=8,CD=6,由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=
-
第2题:
如图,Rt△ABC中,∠ABC=90o,AB=28 cm,以AB为直径的半圆与AC相交,图中的阴影部分①的面积比⑦的面积少28.28 cm2,求BC的长(π取3.14)。
 答案:解析:
答案:解析:
-
第3题:
数学运算。通过运算,选择最合适的一项。
如图,在△ABC中,已知BD=2DC,EC=2AE,则△BFD与△AEF面积的比值为( )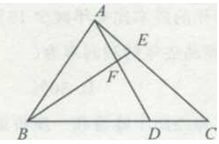 A.4 B.6 C.8 D.9答案:C解析:几何问题。连接CF,因为BD=2DC,EC=2AE,所以设
A.4 B.6 C.8 D.9答案:C解析:几何问题。连接CF,因为BD=2DC,EC=2AE,所以设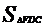 =a,则
=a,则 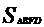 =2a;设
=2a;设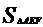 =1,则
=1,则 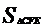 =2。结合图形列方程组得
=2。结合图形列方程组得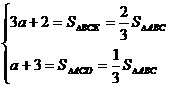 ,两式相除可得a=4。所以
,两式相除可得a=4。所以  ,C项当选。
,C项当选。 -
第4题:
如图所示,在△ABC中,已知AB=AC,AM=AN,∠BAN=30°。问∠MNC的度数是多少?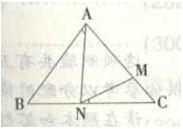 A. 15°
A. 15°
B. 20°
C. 25°
D. 30°答案:A解析:
-
第5题:
在△ABC中,已知AB=5,AC=3,∠A=120°,则BC长为
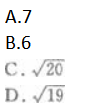 答案:A解析:
答案:A解析: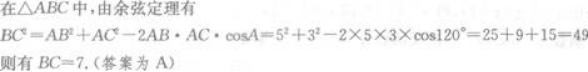
-
第6题:
在△ABC中,AB=2,BC=3,B=60°.求AC及△ABC的面积.答案:解析:解:由余弦定理得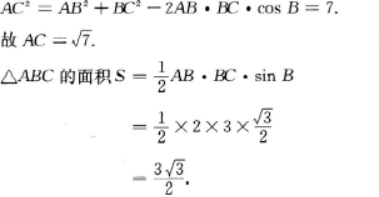
-
第7题:
已知△ABC和△A'B'C'满足AB:A'B'=AC:AC'=2:3,∠A+∠A'=,则△ABC和△A'B'C'的面积比为( ) 答案:E解析:特值法:假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2,S:S'=12*2*2:12*3*3=4:9
答案:E解析:特值法:假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2,S:S'=12*2*2:12*3*3=4:9 -
第8题:
如右图所示,在△ABC:中,D为AC的中点,E在BC上,且 BE : EC=1 : 2,AE与BD交于F。则△BEF与四边形EFDC 的面积之比为( )。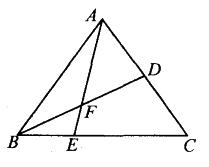
A. 1 : 3 B. 1 : 4
C. 1 : 5 D. 1 : 6答案:C解析: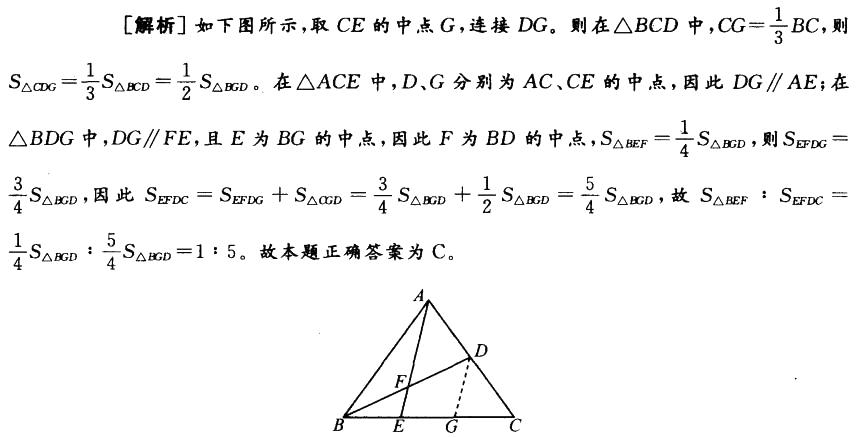
-
第9题:
如图4,在等腰直角△ABC中,∠B=90o,将△ABC绕顶点A逆时针旋转60o后得到△ADE,则∠BAE=__________度。 答案:解析:105
答案:解析:105 -
第10题:
如图,Rt△ABC中,AB=6,BC=4,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为__________。
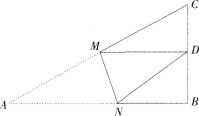 答案:解析:
答案:解析:
-
第11题:
若a,b,c为△ABC的三边之长,则化简的结果为()
- A、a+b-c
- B、b+c-a
- C、a+c-b
- D、a+b+c
正确答案:D -
第12题:
单选题具有激肽样作用的补体裂解片段是()AC2a
BC3a
CC3b
D5a
EBb
正确答案: E解析: 暂无解析 -
第13题:
如图,在Rt△ABC中,∠C=90o,AC=6,BC=8,动点P由起点A沿边AB向终点B运动,每秒2个单位,动点Q由起点B沿边BC向终点C运动,每秒1个单位,P、Q两点同时由起点开始运动,记运动时间为t秒。
(1)设△BPQ的面积为S,求S的最大值:
(2)当△BPQ与△ABC相似时,求t的值。
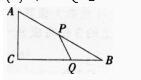 答案:解析:
答案:解析:
-
第14题:
已知两个共用一个顶点的等腰Rt△ABC,等腰Rt△CEF,∠ABC=∠CEF= 90o,连接AF,M是AF的中点,连接MB,ME。
(1)如图1,当CB与CE在同一直线上时,若CB=a,CE=2a,求BM,ME的长;
(2)如图2,当∠BCE=45o时,求证:BM=ME。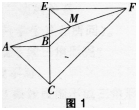
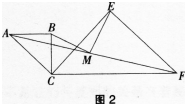 答案:解析:(1)如图,延长AB交CF于点D,则易知△BCD为等腰直角三角形,
答案:解析:(1)如图,延长AB交CF于点D,则易知△BCD为等腰直角三角形,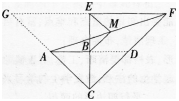

(2)如图,延长AB交CE于点D,连接DF,则△BCD为等腰直角三角形,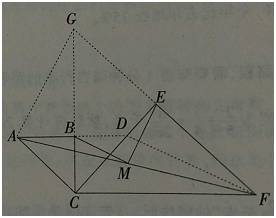
延长FE与CB交于点G,连接AG,则易知△CEG为等腰直角三角形,
∴CE=EF=EG,CF=CG。
∴点E为FG中点。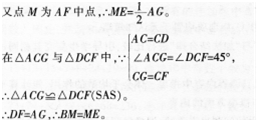
-
第15题:
在△ABC中,BD平分∠ABC,CD平分∠ACB,∠A=50o,则∠BDC=()。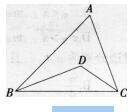 A.100o
A.100o
B.115o
C.120o
D.125o答案:B解析:因为∠A=50°,所以∠ABC+∠ACB=130°,又∵BD平分∠ABC,CD平分∠ACB,所以∠DBC+∠DCB=65°,∠∴BDC=115°。 -
第16题:
如图,在△ABC中,已知BD=2DC,EC=2AE,则△BFD与△AEF面积的比值为( )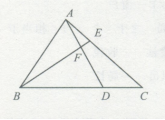 A.4
A.4
B.6
C.8
D.9答案:C解析:C。几何问题。连接CF,因为BD=2DC,EC=2AE,所以设 ,则 ;设 ,则 。结合图形列方程组得 ,两式相除可
得a=4b。所以 ,C项当选。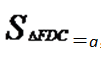
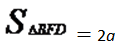

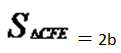

-
第17题:
在△ABC中,AB=2,BC=3,B=60°,BD为AC边上的高.求AC,BD.答案:解析:
-
第18题:
在 ABC中,∠ABC=600,AB=4,BC=6,则AC=()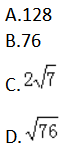 答案:C解析:
答案:C解析: -
第19题:
如图6-9所示,在△ABC中,AD⊥BC于D点,BD=CD,若BC=6,AD=5,则图中阴影部分的面积为( )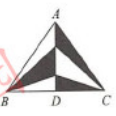 A.3
A.3
B.7.5
C.15
D.30
E.5.5答案:B解析:
-
第20题:
在△ABC中,∠C=90o,AC=8,BC=6,则△ABC的外接圆直径的长为__________ 。答案:解析:10 -
第21题:
如图所示,在△ABC中,AD是∠BAC的平分线,AD = 15,AC=12,CD=9,则点D到AB边的距离是( )。
A. 12 B. 10
C. 9 D.无法确定 答案:C解析:
答案:C解析:



-
第22题:
已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。
正确答案:正确 -
第23题:
判断题已知Rt△ABC中,斜边BC上的高AD=4,cosB=4/5,则AC=5。A对
B错
正确答案: 对解析: 暂无解析
