△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

题目

△ABC中，AB=3，BC=4，则AC边的长满足（ ）。

A．AC=5

B．AC>1

C．AC<7

D．1<AC<7

相似考题

1.在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。A．2.5B．5C．10D．15

2.在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．

3.在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）

4.在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为

参考答案和解析
正确答案：D
三角形的任意两边之和大于第三边，任意两边之差小于第三边，BC-AB=1，BC+AB=7，所以1<AC<7。
更多“△ABC中,AB=3,BC=4,则AC边的长满足( )。 A.AC=5B.AC&gt;1C.AC&lt;7D.1&lt;AC&lt;7 ”相关问题

  • 第1题：

    已知△ABC和△A'B'C'满足AB:A'B'=AC:AC'=2:3,∠A+∠A'=,则△ABC和△A'B'C'的面积比为（ ）


    答案：E
    解析：
    特值法：假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2，S:S'=12*2*2:12*3*3=4:9

  • 第2题：

    如图1，在△ABC中，BC = 8 cm，AB的垂直平分线交AB于点Ｄ， 交边AC于点E，△BCE的周长等于18 cm，则AC的长等于（ ）

    A、6cm　
    B、8cm
    C、10cm　　
    D、12cm

    答案：C
    解析：

  • 第3题：

    1、已知F=A（B’+C)+（A+C)’则其反演式F’=（)。

    A．AC’+A’BC’

    B．AC’+A’B’C

    C．A’C+A’BC’

    D．A’C+ABC’


    结构综合、逻辑综合、版图综合

  • 第4题：

    如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）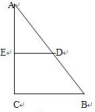



    答案：D
    解析：

  • 第5题：

    在Rt△ABC中，∠C=90°，AB=15，BC：AC=3：4，则BC=_________


    B. 试题分析：在Rt△ABC中，由勾股定理得 ，所以 . 故选A. 考点: 解直角三角形．

相关内容