福建师范大学22春《复变函数》在线作业三及答案参考77
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
C.若正项级数
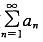 收敛,则
收敛,则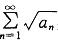 必收敛
必收敛
D.正项级数收敛的充分且必-条件是级数的部分和数列有界
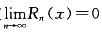 ;选项C,可通过举反例说明,级数
;选项C,可通过举反例说明,级数 收敛,但
收敛,但 发散。
发散。
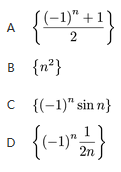

B.收敛数列必单调
C.有界数列必收敛
D.收敛数列必有界

B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
C.若正项级数
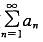 收敛,则
收敛,则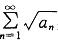 必收敛
必收敛
D.正项级数收敛的充分且必-条件是级数的部分和数列有界
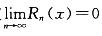 ;选项C,可通过举反例说明,级数
;选项C,可通过举反例说明,级数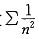 收敛,但
收敛,但 发散。
发散。
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
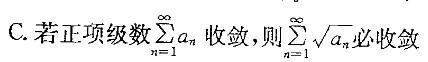
D.正项级数收敛的充分且“条件是级数的部分和数列有界

福建师范大学22春复变函数在线作业三及答案参考1. 下列数列收敛于0的有( ). A,0,0,0, B1, C D下列数列收敛于0的有().A,0,0,0,B1,CDABCD因为这些数列的奇数项和偶数项都收敛于02. 试利用逐项积分法求下列幂级数的和:试利用逐项积分法求下列幂级数的和:提示 其答案依次为: 3. 计算mod5的整数的加法表、乘法表和减法表。计算mod5的整数的加法表、乘法表和减法表。 oplus 0 1 2 3 4 0 0 1 2 3 4 1 1 2 3 4 0 2 2 3 4 0 1 3 3 4 0 1 2 4 4 0 1 2 3 otimes 0 1 2 3 4 0 0 0 0 0 0 1 0 1 2 3 4 2 0 2 4 1 3 3 0 3 1 4 2 4 0 4 3 2 1 ominus 0 1 2 3 4 0 0 4 3 2 1 1 1 0 4 3 2 2 2 1 0 4 3 3 3 2 1 0 4 4 4 3 2 1 0 4. 任意给定Cnn中的矩阵范数M,则存在Cn中的向量范数v,使得对任意的ACnn和任意的xCn都有 AxvAM任意给定Cnn中的矩阵范数M,则存在Cn中的向量范数v,使得对任意的ACnn和任意的xCn都有AxvAMxv(1.16)取非零列向量yCn,定义xv=xyHM,则v是Cn中的向量范数,且满足式(1.16) 证毕 5. 设A,B,C为任意集合,试证: (1)A(BC)=(AB)(AC); (2)A(BC)=(AB)(AC)设A,B,C为任意集合,试证:(1)A(BC)=(AB)(AC);(2)A(BC)=(AB)(AC)分析上述等式左边是表示先做括号内的并、交运算,再做笛卡尔乘积;而等式右边则表示先做括号内的笛卡尔乘积,再做并、交运算它们的结果应该是一样的,可以用笛卡尔乘积和并、交运算的定义及括号的优先级别来证明,这是集合等式证明中常见的一种基本方法 证明 (1)A(BC)=(x,y)| xA且yBC =(x,y) xA且yB或xA且yC =(x,y)|(x,y)AB或(x,y)AC =(x,y)|(x,y)(AB)(AC) =(AB)(AC); (2)A(BC)=(x,y)| xA且yBC =(x,y)| xA且yB且xA且yC =(x,y)|(x,y)AB且(x,y)AC =(x,y)|(x,y)(AB)(AC) =(AB)(AC) 6. 初等函数是否必定存在原函数?初等函数是否必定存在原函数?7. 求下列函数的极值: (1) yx55x1; (2) yxlnx; (3) yx2x1求下列函数的极值: (1) yx55x1; (2) yxlnx; (3) yx2x1正确答案:解 (1) D(f)()y5x45 令y0得驻点x11x21rn列表rn解(1)D(f)(,),y5x45令y0得驻点x11,x21列表8. 设随机变量X的分布律为 X 0 p 0.4 r 0.1设随机变量X的分布律为X0p0.4r0.1且E(X)=0,D(X)=2,试求待定系数,r,其中由离散型随机变量分布律的性质得1=0.4+r+0.1r=0.5 又由数学期望与方差的定义得 E(X)=0=0.4+00.5+0.10.4+0.1=0=-4, D(X)=2=0.4(-0)2+0.5(0-0)2+0.1(-0)20.42+0.12=2,解得=1,=4 又,故=-1,=4,r=0.5小结随机变量的分布律(或概率密度)的性质、数学期望和方差的定义在确定待定系数的题目中经常用到,要灵活掌握三者之间的相互转化关系 9. 试证明: 设且m(E)+,若fk(x)在E上依测度收敛于f(x),且f(x)0,fk(x)0,aexE(kN),则1/fk(x)在E上依测度试证明:设且m(E)+,若fk(x)在E上依测度收敛于f(x),且f(x)0,fk(x)0,aexE(kN),则1/fk(x)在E上依测度收敛于1/f(x).证明 不妨假定fk(x)(kN)与f(x)皆不为0依题设知,对任一子列fki(x),均存在子列fkij(x)几乎处处收敛于f(x)也就是说,对任一子列1/fk(x),均存在子列1/fkij(x)几乎处处收敛于1/f(x).这说明命题结论成立.10. 对积分上限的函数求导时应注意些什么?对积分上限的函数求导时应注意些什么?(1)首先要弄清是对哪个变量求导,把积分上限的函数的自变量与积分变量区分开来积分上限的函数的自变量是上限变量,因此对积分上限的函数求导,就是对上限变量求导,与积分变量没有关系但有时会遇到上限变量也含在被积表达式内的情况,这时应先设法把上限变量从被积表达式内分离出来,并提到积分号外,然后再进行求导,例如上个问题中的,对它求导时,应先把它写作,然后应用乘积的求导公式求导 (2)当积分上限,甚至积分下限,都是x的函数时,就要应用复合函数的求导法则进行求导一般说来,有下述结果(证明从略): 当函数(x),(x)均在a,b上可导,函数f(x)在a,b上连续时,则有 =(x)f(x)-(x)f(x) 11. 证明每个结点的次数至少为2的图必包含一个回路证明每个结点的次数至少为2的图必包含一个回路设L是图G中最长路中的一条,设其长度为m,这条路的一个端点设为a,考察G中与a关联的那些边,这些边中任何一条边的另一端必在L上,否则,将这个结点加进L中就可得到一条更长的路 如果G中每个结点的次数至少为2,那么a也要关联于一条不在L上的边e,若e是环,则e本身就是回路,否则,边e的另一个端点b(与a不同的点)在L上,而连通L中a到b的子通路与边e就组成一个回路本题证明时所设L是考虑了能否构成环的最坏情况(见图(a),除两头外,其他结点的次数为2(满足至少为2的最少次数情况),如果不按L来安排结点在图中位置的话,已经可出现回路 由于条件给出每个结点的次数至少为2,那么结点a及L中的另一端点的次数就不会是1,故会有如图(b)所示的情况由a引出的另一条边e的另一头必会去与另一结点相连(如结点b,因为按最差情形所有点均放到了L上),此时已出现了回路 12. 两个本原多项式g(x)和h(x)若在Qx中相伴,那么g(x)h(x)等于多少?A、1B、任意常数cC、任意有理数两个本原多项式g(x)和h(x)若在Qx中相伴,那么g(x)/h(x)等于多少?A、1B、任意常数cC、任意有理数D、任意实数正确答案: A13. 证明:当n3时,全体3一循环是交代群An的一个生成系证明:当n3时,全体3一循环是交代群An的一个生成系正确答案:n=3时结论显然成立因此下设n3rn 由于An中每个元素都可表为偶数个对换之积从而也就是一些形如rn (ab)(cd)或(ab)(ac)的项之积其中abcd是12n中互异的元素但由于rn (ab)(cd)=(abc)(bcd) (ab)(ac)=(acb)rn故An中的每个元素又都是一些3一循环之积即An由全体3一循环生成n=3时,结论显然成立因此下设n3由于An中每个元素都可表为偶数个对换之积,从而也就是一些形如(ab)(cd)或(ab)(ac)的项之积其中a,b,c,d是1,2,n中互异的元素但由于(ab)(cd)=(abc)(bcd),(ab)(ac)=(acb),故An中的每个元素又都是一些3一循环之积,即An由全体3一循环生成14. 试证明: 设fn(x是R1上非负渐降连续函数列若在有界闭集F上fn(x)0(n),则fn(x)在F上一致收敛于零试证明:设fn(x是R1上非负渐降连续函数列若在有界闭集F上fn(x)0(n),则fn(x)在F上一致收敛于零证明 由题设可知,对任意的xF以及0,存在自然数指标n,使得fn(x)因为f(x)是连续函数,所以存在x0,使得fn(t)(tB(x,x)注意到B(x,x)是F的开覆盖,故存在有限个开球 B(xi,xi) (i=1,2,m), 记与xi相应的自然数指标为ni(i=1,2,m),则令N=maxn1,n2,nm,我们得到 fn(x) (nN,xF) 这说明fn(x)在F上一致收敛于0 15. 具有特解y1=e-x,y2=2xe-x,y3=3ex的3阶常系数齐次微分方程是( ) Ay&39;-y-y&39;+y=0 By具有特解y1=e-x,y2=2xe-x,y3=3ex的3阶常系数齐次微分方程是()Ay-y-y+y=0By+y-y-y=0Cy-6y+11y-6y=0Dy-2y-y+2y=0B将y1=ev代入上述四个选项,可将(C)淘汰 将y2=2xe-x代入其余三个选项,可知,仅有(B)正确,且y3=3ex亦满足(B) 16. 若A 和B都是R中开集,且A是B的真子集,则( )A.m(A)m(B)B.m(A)=m(B)C.m(BA)=m(A)D.m(B)=m(A)+m(BA)参考答案:BD17. 试证试证(sinh z)=cosh z;(cosh z)=sinh z试证(sinh z)=cosh z;(cosh z)=sinh z正确答案:
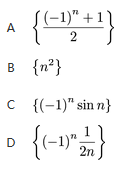

 的收敛域及和函数.
的收敛域及和函数.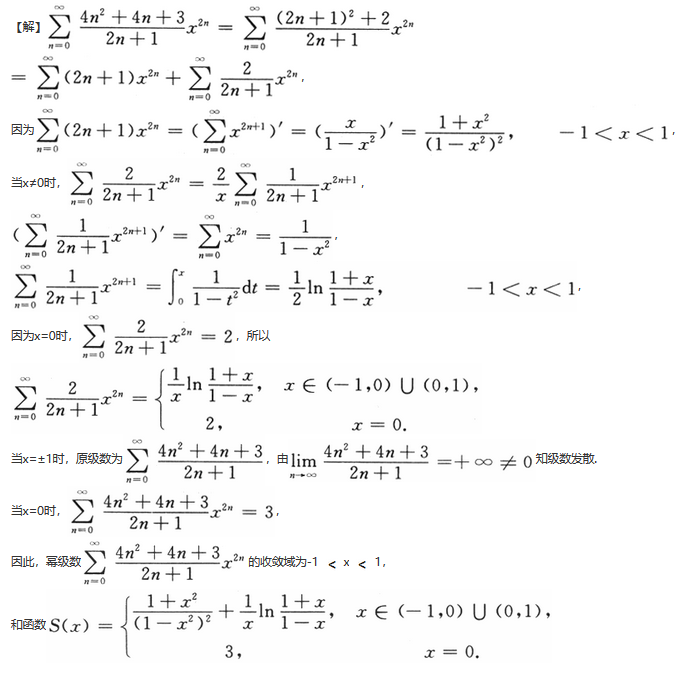
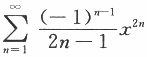 的收敛域及和函数
的收敛域及和函数
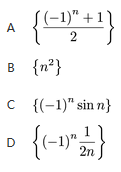

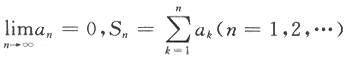 无界,则幂级数
无界,则幂级数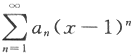 的收敛域为
的收敛域为B.[-1,1)
C.[0,2)
D.(0,2]

更多 “福建师范大学22春《复变函数》在线作业三及答案参考77” 相关考题
相关内容
最新试卷
热门试卷
- 重庆大学22春《建筑节能》在线作业三及答案参考87-
- 重庆大学22春《建筑结构》抗震在线作业二及答案参考15-
- 重庆大学22春《建筑节能》在线作业三及答案参考64-
- 重庆大学22春《建筑结构》在线作业二及答案参考91-
- 重庆大学22春《建筑节能》在线作业三及答案参考48-
- 南开大学2021年12月《销售风险管理与实务》期末考核试题库及答案参考14-
- 重庆大学22春《建筑结构》在线作业二及答案参考18-
- 重庆大学2021年12月《高电压技术》期末考核试题库及答案参考65-
- 西安交通大学2021年12月《病理学》期末考核试题库及答案参考53-
- 西安交通大学2021年12月《病理学》期末考核试题库及答案参考17-
