单选题数列1，0，1/2，0，1/3，…，0，1/n，……（）。A 收敛于2B 收敛于1C 收敛于0D 发散

题目
单选题
数列1，0，1/2，0，1/3，…，0，1/n，……（）。
A

收敛于2

B

收敛于1

C

收敛于0

D

发散

相似考题

1.（ 12 ）已知数列的递推公式如下：f(n)=1 当 n=0,1 时f(n)=f(n-1)+f(n-2) ? 当 n>1 时则按照递推公式可以得到数列： 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …… 。现要求从键盘输入 n值，输出对应项的值。例如当输入 n 为 8 时，应该输出 34 。程序如下，请补充完整。Private Sub runl1_Click( )f0=1f1=1num=Val(InputBox(" 请输入一个大于 2 的整数 : "))For n=2 To____ 【 12 】 _______f2= ___ 【 13 】 ________f0=f1f1=f2Next nMsgBox f2End Sub

2.已知数列{an}满足an=3n+1(n为奇数，n∈N) 2n-2（n为偶数，n∈N）则a2·a3=（ ）。A．70B．28C．20D．8

3.已知数列的递推公式如下：f(n)＝1 当n＝0，1时f(n)＝f(n-1)+f(n-2) 当n＞1时则按照递推公式可以得到数列：1，1，2，3，5，8，13，21，34，55，……。现要求从键盘输入n值，输出对应项的值。例如当输入n为8时，应该输出34。程序如下，请补充完整。Private Sub runll_Click()f0=1f1=1num=Val(InputBox("请输入一个大于2的整数："))For n=2 To 【 】f2＝【 】f0=f1f1=f2Next nMsgBox f2End Sub

4.设X~N(0,1),Y~N(0,1),且X与Y相互独立,则X＋Y服从的分布为()A、X+Y服从N(0，1)B、X+Y不服从正态分布C、X+Y~X2(2)D、X+Y也服从正态分布

参考答案和解析
正确答案： C
解析： 暂无解析
更多“数列1，0，1/2，0，1/3，…，0，1/n，……（）。”相关问题

  • 第1题：

    数字推理。给你一个数列，但其中缺少一项。要求你仔细观察数列的排列规律。然后从四个供选择的选项中选择你认为最合理的一项，来填补空缺项。使之符合原数列的排列规律。

    3，3，-1，0，1，( )，2，11。

    A．-3

    B．4

    C．7

    D．5


    正确答案：D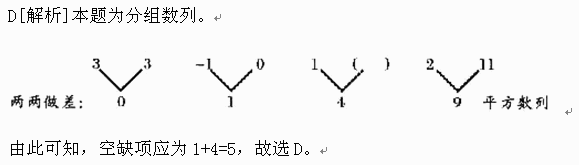

  • 第2题：

    “对任意给定的ε∈(0，1)，总存在正整数N，当n>N时，恒有｜xn-a｜≤2ε”是数列{xn}收敛于a的


    A.充分条件但非必要条件
    B.必要条件但非充分条件
    C.充分必要条件
    D.既非充分条件又非必要条件


    答案：C
    解析：
    本题主要考查考生对数列极限的ε-N定义的理解.其定义是“对任意给定的ε>0，总存在正整数N，当n>N时，恒有｜xn-a｜<ε”显然，若｜xn-a｜<ε，则必有｜xn-a｜≤2ε，但反之也成立，这是由于ε的任意性，对于任意给定的ε1>0，取｜xn-a｜≤2ε中的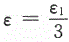，则有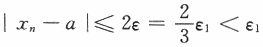即，对任意给定的正数ε1>0，总存在正整数N，当n>N时，恒有｜xn-a｜<ε1，故应选(C).　　【评注】到目前为止，考研试卷中还没考过利用极限定义证明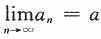，或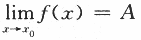的试题，但从本题可看出，要求考生理解极限的定义.

  • 第3题：

    创建一个范围在(0,1)之间的长度为12的等差数列, 可以使用 ________ 。


    答案：
    解析：
    1、np.linespace()

  • 第4题：

    已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为（ ）

    A.248
    B.168
    C.128
    D.19
    E.以上选项均不正确

    答案：B
    解析：

  • 第5题：

    在体心立方晶胞中，体心原子的坐标是（）。

    A.1/2，1/2，0
    B.1/2，0，1/2
    C.1/2，1/2，1/2
    D.0，1/2，1/2

    答案：C
    解析：

  • 第6题：

    (10分)已知数列{an}满足a1=3，an+1= an +2n，
    (1)求{ an }的通项公式an；
    (2)若bn=n an，求数列{bn}的前n项和sn。


    答案：
    解析：

  • 第7题：

    数列1，0，1/2，0，1/3，…，0，1/n，……（）。

    • A、收敛于2
    • B、收敛于1
    • C、收敛于0
    • D、发散

    正确答案:C

  • 第8题：

    设（X1，X2，…，X）是抽自正态总体N（0，1）的一个容量为n的样本，记，则下列结论中正确的是（）。

    • A、服从正态分布N（0，1）
    • B、n服从正态分布N（0，1）
    • C、服从自由度为n的x2分布
    • D、服从自由度为（n-1）的t分布

    正确答案:C

  • 第9题：

    在移动平均中，设移动n年则（）。

    • A、当n为偶数时，移动后所得新数列较原数列首尾各缺n∕2项
    • B、当n为奇数时，移动后所得新数列较原数列首尾缺（N-1）∕2项
    • C、当n为偶数时，移动后所得新数列较原数列首尾缺n项
    • D、当n为奇数时，移动后所得新数列较原数列首尾缺n项

    正确答案:A,B

  • 第10题：

    单选题
    设（X1，X2，…，X）是抽自正态总体N（0，1）的一个容量为n的样本，记，则下列结论中正确的是（）。
    A

    服从正态分布N（0，1）

    B

    n服从正态分布N（0，1）

    C

    服从自由度为n的x2分布

    D

    服从自由度为（n-1）的t分布


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    np.linspace（-1，1，2）输出结果为：（）
    A

    array（[-1，1]）

    B

    array（[-1，0，1]）

    C

    array（[-1，0]）

    D

    array（[0，1]）


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    设集合M＝{－1，0，1，2，8}，N＝{x|x≤2}，则M∩N＝（　　）．
    A

    {0，1，2}

    B

    {－1，0，1}

    C

    {－1，0，1，2}

    D

    {0，1}


    正确答案： D
    解析：
    所求M∩N是M中所有满足条件x≤2的元素组成的集合，易知元素－1，0，1，2均满足条件，所以M∩N＝{－1，0，1，2}．

  • 第13题：

    设Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，为样本均值，则的分布可以表示为( )。

    A．N(0，1/2)

    B．N(0，4)

    C．N(0，1/4)

    D．概率密度为

    E．N(0，1/8)


    正确答案：CD
    解析：因Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，所以其均值也服从正态分布，且均值为0，标准差为；将μ=0，σ=1/2代入正态分布的概率密度函数p(x)=，-∞x∞，可得的概率密度为。

  • 第14题：

    请选择你认为最为合理的一项，来填充所给数列的空缺项，使之符合原数列的排列规律：0，1/3 ，6/11 ，7/10 ，（ ）， 31/35


    A. 29/30
    B. 29/33
    C. 31/36
    D. 30/37

    答案：D
    解析：
    30/37

    0/ 3 2/6 6/11 14/20 30/37 62/70

    分母减分子，3,4,5,6,7,8

  • 第15题：

    设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,


    答案：
    解析：
    【解】因为X，Y相互独立且都服从正态分布，所以X，Y的线性组合仍服从正态分布，即2=2X-Y+3服从正态分布，由E(Z)=2E(X)-E(Y)+3=5，D(Z)=4D(X)+D(Y)=9，则Z的密度函数为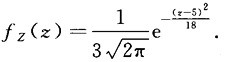

  • 第16题：

    在fcc晶胞中，八面体间隙中心的坐标是（）。

    A.1/2，1/2，0
    B.1/2，0，1/2
    C.0，1/2，1/2
    D.1/2，1/2，1/2

    答案：D
    解析：

  • 第17题：

    若不等式x2-x≤0的解集为M，函数?(x)=In(1-|x|)的定义域为N，则M∩N为()．?

    A.[0，1)
    B.(0，1)
    C.[0，1]
    D.(-1，0]

    答案：A
    解析：
    M={x|x2-x≤0}={x{0≤x≤1}，N={x|1-|x|>0}={x|-1

  • 第18题：

    已知数列{an}满足a1=2，an+1=3an+2(n∈N*)，
    (1)求数列{an}的通项公式；



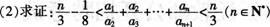    答案：
    解析：

  • 第19题：

    几何平均数是指（）。

    • A、分布数列中n个标志值的连乘积的n次方根
    • B、分布数列中n个标志值的连相加的n次方根
    • C、分布数列中n个标志值的连相减的n次方根
    • D、分布数列中n个标志值的连开方的n次方根

    正确答案:A

  • 第20题：

    设随机变量X~N（0，1），Y=aX+b（a＞0），则（）

    • A、Y~N（0，1）
    • B、Y~N（b，a）
    • C、Y~N（b，a2）
    • D、Y~N（a+b，a2）

    正确答案:C

  • 第21题：

    单选题
    数列1，0，1/2，0，1/3，…，0，1/n，……（）。
    A

    收敛于2

    B

    收敛于1

    C

    收敛于0

    D

    发散


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    “对任意给定的ε∈（0，1），总存在正整数N，当n≥N时，恒有|xn－a|≤2ε”是数列{xn}收敛于a的（　　）。
    A

    充分条件但非必要条件

    B

    必要条件但非充分条件

    C

    充分必要条件

    D

    既非充分又非必要条件


    正确答案： A
    解析：
    对于任意给定的ε＞0，总∃正整数N，使当n＞N时，|xn－a|＜ε，则称数列{xn}收敛于a。这是数列的极限的精确定义。其中，ε要任意小，才能使|xn－a|任意小。题目可改为：对任意ε1＝2ε∈（0，2）＞0，总∃正整数N1，使当n≥N＞N1时，|xn－a|＜2ε＝ε1，则称{xn}收敛于a，其中ε1∈（0，2）可以任意小，则|xn－a|可以任意小，这两种说法是等价的。

  • 第23题：

    单选题
    在体心立方晶胞中，体心原子的坐标是（）。
    A

    1/2，1/2，0

    B

    1/2，0，1/2

    C

    1/2，1/2，1/2

    D

    0，1/2，1/2


    正确答案： B
    解析： 暂无解析

  • 第24题：

    单选题
    设X～N（0，1），则X2服从（）．
    A

    χ2（n）

    B

    χ2（1）

    C

    t（1）

    D

    N（0，1）


    正确答案： B
    解析： 暂无解析

相关内容