苏教版初中数学八年级上第一学期第3周周考试卷

请教:2012年初中数学第7章三角形综合检测题A(七年级下)第1大题第5小题如何解答?

【题目描述】

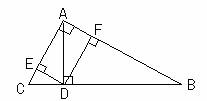
如图，在直角三角形ABC中，AC≠AB，AD是斜边上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角的个数是（）

A、3个 B、4个 C、5个 D、6个

【参考答案与解析】：

正确答案：B

答案分析：

就是三个吧

∠ADE,∠DAB,∠BDF
应该只有3个，可能答案有问题吧。

二、判断题（本大题共4小题，每题2分，共8分）

第 12 题三角形中最大的一个角是70。，按角分类这是一个锐角三角形。（）

正确答案：√

在等腰三角形ABC中，A是顶角，且cosA=-21，则cosB=（）

A.A

B.B

C.C

D.D

正确答案：B
本题主要考查的知识点为三角函数式的变换．【应试指导】

如图．△ABC是一个等腰直角三角形，它与一个正方形叠放在一起，已知AE=EF=FB，⊿EFD的面积是4 cm2，则⊿ABC的面积是________cm2。

答案：

解析：

在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一条射线CM，与线段AB交于点M，则AC>AM的概率是______。

答案：

解析：

苏教版初中数学八年级上册第一学期第3周周考试卷一、选择题（每题4分，共28分）1. 在ABC中， C=B，与ABC全等的三角形有一个角是100，那么ABC中与这个角对应的角是 ( )AB BA CC DB或C2. 如图，已知AB=AD，那么添加下列一个条件后，仍无法判定ABCADC的是( )ACB=CD BBAC=DACCBCA=DCA DB=D=90 第2题图第3题图3. 如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是 ( )A.SSS B.SAS C.AAS D.ASA 4. 如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD相交于点O，且ABAD，则下列判断不正确的是 ( )AABDCBD B ABCADC CAOBCOB DAODCOD 第4题图第5题图5. 如图，点B、C、E在同一条直线上，ABC与CDE都是等边三角形，则下列结论不一定成立的是 ( )AACEBCD BBGCAFC CDCGECF DADBCEA 6.A 在ABC中，A=90，CD平分ACB，DEBC于点E，若AB=6，则DE+DB= ( )A4 B. 5 C. 6 D. 7 第6题图第7题图7. 如图，已知点C是AOB的平分线上一点，点P、P分别在边OA、OB上如果要得到OP=OP，需要添加以下条件中的某一个即可，请你写出所有可能的结果的序号为 ( )OCP=OCP；OPC=OPC；PC=PC；PPOCA. B. C. D.二、填空题（每题4分，共28分）8.A 如图，ABCADE，B=100，BAC=30，那么AED=_ 第8题图第9题图 9.A如图，1=2，要使ABEACE，还需添加一个条件是（填上你认为适当的一个条件即可）.10.A 如图，AE=BF，ADBC，AD=BC，则有ADF ，且DF= . 第10题图第11题图11 如图，ABC中，ADBC于D，要使ABDACD，若根据“HL”判定，还需要加条件，若加条件B=C，则可用判定12 把两根钢条AA、BB的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳），如图，若得AB=5厘米，则槽为厘米第12题图第13题13.A如图，AD=AE，BE=CD，1=2=100，BAE=60，那么CAE=_. 第14题图 14.如图，A=E， ACBE，AB=EF，BE=10，CF=4，则AC=_.三、解答题（共44分）15.（10分）A 已知：如图，ABC=DCB，BD、CA分别是ABC、DCB的平分线求证：AB=DC 16.（10分）A 两块完全相同的三角形纸板ABC和DEF，按如图所示的方式叠放，阴影部分为重叠部分，点O为边AC和DF的交点.不重叠的两部分AOF与DOC是否全等？为什么？ 17. （10分）A如图，DCE=90，CD=CE，ADAC，BEAC，垂足分别为A、B求证：AD+AB=BE 18 .（14分）如图A、E、F、C在一条直线上，AE=CF，过E、F分别作DEAC，BFAC，若AB=CD（1）图中有对全等三角形，并把它们写出来（2）求证：BD与EF互相平分于G；（3）若将ABF的边AF沿GA方向移动变为图时，其余条件不变，第（2）题中的结论是否成立，如果成立，请予证明

用铁皮剪成两个三角形：
①如果剪成顶角相等，并且有一条腰相等的两个等腰三角形，则它们全等。
②如果都有一个角等于42°，且有两边相等，则它们全等。
③如果在剪成的△ABC和△A1B1C1中，∠C=∠C1＝90°，那么不论是BC=B1C1,AC=A1C1，还是BC=B1C1，AC=B1C1，剪的两个三角形都全等。
上面说法中，正确的是（）。

A. ①
B. ①②
C. ②③
D. ①③

答案：D

解析：

［解析］根据三角形角边角规则，①③正确，②错误。

在△ABC中，若

则△ABC必是( )

A.直角三角形
B.等腰三角形
C.等边三角形
D.钝角三角形

答案：C

解析：

【考情点拨】本题主要考查的知识点为等式的变换．【应试指导】

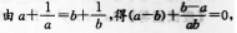
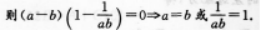
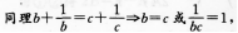
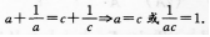
∴a=b=C．

△ABC中，已知acosA=bcosB，则△ABC是

A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰三角形或直角三角形

答案：D

解析：

在相似三角形的判定的复习课上，甲乙两位教师分别设计了如下的教学片段：

（甲教师）

问题引入：如图1，在△ABC中，D、E分别是AB、AC上的两点，请你另外添加一个条件，使△ABC∽△ADE，并说明添加条件的理由。

预设学生回答。

（1）添加一个条件，∠ADE=∠B

（2）添加一个条件，∠AED=∠C

（5）依次说出判定方法和理由。

（乙教师）

教师提问：判定三角形相似有哪些方法？

预设学生回答：

（1）两角分别相等的两个三角形相似；

（2）两边成比例且夹角相等的两个三角形相似；

（3）三边成比例的两个三角形相似。

针对上述材料，完成下列任务。

（1）请分别对两位教师的教学设计片段进行评价，并简述理由。（10分）

（2）为了进一步巩固三角形相似的判定定理，请设计开放性的例题和习题各一个，并简述理由。（10分）

（3）简述数学教学中例题和习题设计的注意事项。（10分）

答案：

解析：

本题主要考查数学教学设计内容。

1.分析两位教师的教学设计过程，针对不同内容给出对应的评价；2.根据教学要求及教学目标设计相应的例题与习题。

在相似三角形的判定的复习课上．甲乙两位教师分别设计了如下的教学片段：
(甲教师)
问题引入：如图1，在△ABC中，D、E分别是AB、AC上的两个点，请你另外添加一个条件，使△ABC—AADE．并说明添加条件的理由。
预设学生回答。
(1)添加一个条件

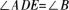
(2)添加一个条件

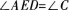
(3)添加一个条件

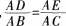
(4)添加一个条件

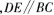
(5)…………依次说出判定方法和理由。
(乙教师)
教师提问：判定三角形相似有哪些方法
预设学生回答：
(1)两角分别相等的两个三角形相似；
(2)两边成比例且夹角相等的两个三角形相似；
(3)三边成比例的两个三角形相似。
针对上述材料，完成下列任务。
(1)请分别对两位教师的教学设计片段进行评价，并简述理由。(10分)
(2)为了进一步巩固三角形相似的判定定理，请设计开放性的例题和习题各一个，并简述理由。(10分)
(3)简述数学教学中例题和习题设计的注意事项。(10分)

答案：

解析：

(1)两位教师的教学片段均属于课堂提问的类型。教师甲是应用提问。这种提问的目的是了解学生能否在理解新知识的基础上应用新知识和旧知识来解决问题。而教师乙采用的是复习、回忆提问。通过复习，回忆提问，使新旧知识相互连贯，强化了所学知识，还能检查学生的复习情况。
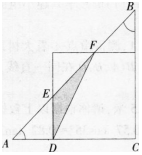
(2)例题：如图2在AABC中，点D，E分别在AB，AC边上，连结DE并延长交BC的延长线于点F，连结DC，BE，若∠BDE+∠BCE=1800

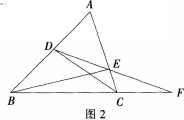
①写出图中三对相似三角形(注意：不得加字母和线)
②请在你所找出的相似三角形中选取一对，说明他们相似的理由。
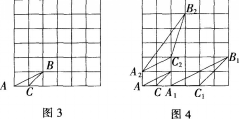
习题：如图3，已知格点AABC，请在图4中分别画出与△ABC相似的格点△A1B1C1和格点△A2B2C2，并使△A1B1C1和△ABC的相似比等于2，而△ABC和△ABC的相似比等于根号5。(说明：顶点都在网格线交点处的三角形叫做格点三角形，友情提示：请在画出的三角形的顶点处标上相应的字母。)

理由：两道例题设计具有梯度，难度逐渐增加，例l在老师的引导下充分巩固了三角形相似的性质，练习题设置具有开放性，能够充分发挥学生的创造力，调动学生主动思考的积极性。
(3)例题设计应具有目的性、典型性、启发性、科学性、变通性和有序性。具体来说，例题的选择要从学习目标和任务出发进行精选；要根据学生的学情进行例题的选配和安排，学习新知识必须建立在已有知识基础之上；更要具有提炼性。
习题是数学课堂教学的一个重要组成部分，他不仅有助于学生对知识的理解，巩固形成熟练的技能技巧，而且对学生智力发展和能力提高起着重要的作用，所以习题的设计应具有目的性、要及时、要有层次、要多样化、要有反馈。

苏教版初中数学八年级上第一学期第3周周考试卷

更多 “苏教版初中数学八年级上第一学期第3周周考试卷” 相关考题

相关内容

最新试卷

热门试卷