设0≤an≤1/n(n=1,2,…)，下列级数中绝对收敛的是（ ）。

题目
设0≤an≤1/n(n=1,2,…)，下列级数中绝对收敛的是（ ）。

相似考题

1.下列级数中绝对收敛的级数是(64)。A．B．C．D．

2.设X～N(μ，σ2)，σ未知，xi为样本(i=1，2，…，n)。H0:μ≤μ0，H1:μ＞μ0，α为显著性水平，则接受域( )。

3.设Xi(i＝1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。A．若Xi(i＝1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布B．若Xi(i＝1，2，…，n)服从指数分布，且λ相同，则服从正态分布C．若Xi(i＝1，2，…，n)服从[a，b]上的均匀分布，则服从正态分布D．无论Xi(i＝1，2，…，n)服从何种相同的分布，其均值都服从正态分布

4.设X～N(μ，σ2)，σ未知，xi为样本(i＝1，2，…，n)，H0:μ=μ0，Hi:μ≠μ0，a为显著性水平，则接受域为( )。A．t＜t1-a(n-1)B．t＞ta(n-1)C．D．以上都不对

参考答案和解析
答案：C
解析：
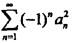提示：因为0n≤1/n(n=1,2,…)，所以0≤an2≤1/n2，故绝对收敛。
更多“设0≤an≤1/n(n=1,2,…)，下列级数中绝对收敛的是（ ）。 ”相关问题

  • 第1题：

    设Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，为样本均值，则的分布可以表示为( )。

    A．N(0，1/2)

    B．N(0，4)

    C．N(0，1/4)

    D．概率密度为

    E．N(0，1/8)


    正确答案：CD
    解析：因Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，所以其均值也服从正态分布，且均值为0，标准差为；将μ=0，σ=1/2代入正态分布的概率密度函数p(x)=，-∞x∞，可得的概率密度为。

  • 第2题：

    设an>0(n=1，2，…)，Sn=a1+a2+…+an，则数列{Sn}有界是数列{an}收敛的

    A.充分必要条件
    B.充分非必要条件
    C.必要非充分条件
    D.既非充分也非必要条件

    答案：B
    解析：

  • 第3题：

    设任意项级数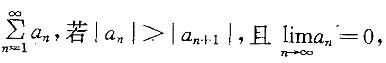则对该级数下列哪个结论正确？
    A.必条件收敛 B.必绝对收敛
    C.必发散 D.可能收敛，也可能发散


    答案：D
    解析：
    提示:举例说明，级数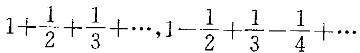均满足条件，但前面级数发散，
    后面级数收敛，敛散性不能确定。

  • 第4题：

    设X~N(μ，σ2)，σ已知，xi为样本（i= 1，2，…，n）。 H0：μ=μ0 ， H1：μ≠μ0 ，则检验统计量指的是（ ）。


    答案：B
    解析：
    对于单个正态总体，当总体方差σ2已知时，均值μ的检验统计量为。

  • 第5题：

    设X1,X2,…,Xn（n>2）是来自总体X～N(0,1)的简单随机样本,记Yi=Xi-（i=1,2,…,n）.求：(1)D(Yi);(2)Cov(Yb,Yn).


    答案：
    解析：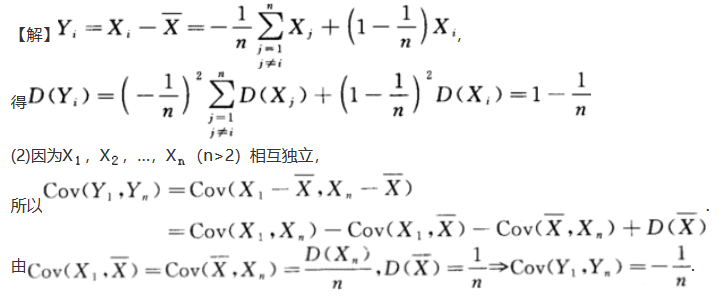

  • 第6题：

    设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
    　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).


    答案：
    解析：

  • 第7题：

    设un≤vn(n=1，2，…)，则（）



    答案：D
    解析：
    un、vn可能为任意数值，因此正项级数的比较判别法不能成立，可知应选D．

  • 第8题：

    若设w表示权重，Wi表示第i项指标的权重，在同一层次上指标应满足（）。

    A0

    B0≤Wi<1，对i=1，2，…，n求和：∑Wi=1

    CWi=1，对i=1，2，…，n求和：∑Wi=1

    D0≤Wi≤1，对i=1，2，…，n求和：∑Wi=0


    A
    略

  • 第9题：

    标准正态分布的表示方法是（）

    • A、N（1，0）
    • B、N（0，1）
    • C、N（1，1）
    • D、N（0，0）
    • E、N（1，2）

    正确答案:B

  • 第10题：

    设p是一个素数，且p≡-1（mod4）则Zp的所有非零平方元的集合D是Zp的加法群的什么差集？（）

    • A、（4n-1，2n，n）
    • B、（4n-1，2n-1，n-1）
    • C、（4n+1，2n-1，n-2）
    • D、（4n-1，2n+1，n-3）

    正确答案:B

  • 第11题：

    单选题
    若设w表示权重，Wi表示第i项指标的权重，在同一层次上指标应满足（）。
    A

    0

    B

    0≤Wi<1，对i=1，2，…，n求和：∑Wi=1

    C

    Wi=1，对i=1，2，…，n求和：∑Wi=1

    D

    0≤Wi≤1，对i=1，2，…，n求和：∑Wi=0


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    设p是一个素数，且p≡-1（mod4）则Zp的所有非零平方元的集合D是Zp的加法群的什么差集？（）
    A

    （4n-1，2n，n）

    B

    （4n-1，2n-1，n-1）

    C

    （4n+1，2n-1，n-2）

    D

    （4n-1，2n+1，n-3）


    正确答案： D
    解析： 暂无解析

  • 第13题：

    设Xi (i=1，2，…，n)为n个相互独立的随机变量，则下列结论成立的是( )。

    A．若Xi (i=1，2，…，n)服从正态分布，且分布参数相同，则服从正态分布

    B．若Xi (i=1，2，…，n)服从指数分布，且λ相同，则服从正态分布

    C．若Xi(i=1，2，…，n)服从[a，b)上的均匀分布，则服从正态分布

    D．无论Xi (i=1，2，…，n)服从何种分布，其均值都服从正态分布


    正确答案：A
    解析：若总体服从正态分布，无论样本量大小，其样本均值X都服从正态分布。

  • 第14题：

    下列级数中，绝对收敛的级数是（　　）。



    答案：D
    解析：
    可将各项分别取绝对值后判别敛散性。A项，取绝对值后为调和级数，发散；B项，取绝对值后为p级数，且p=1/2＜1，发散；C项，由

  • 第15题：

    下列级数中，绝对收敛的是（　　）．



    答案：A
    解析：

  • 第16题：

    设X,Y相互独立,且X～N(1,2),Y～N(0,1),求2=2X－Y＋3的密度函数,


    答案：
    解析：
    【解】因为X，Y相互独立且都服从正态分布，所以X，Y的线性组合仍服从正态分布，即2=2X-Y+3服从正态分布，由E(Z)=2E(X)-E(Y)+3=5，D(Z)=4D(X)+D(Y)=9，则Z的密度函数为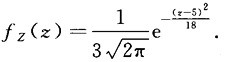

  • 第17题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第18题：

    级数 ( )。
    A.当p>1/2时，绝对收敛 B.当p>1/2时，条件收敛
    C.当0


    答案：A
    解析：
    提示：取绝对值后是p级数，2p>1绝对收敛。

  • 第19题：

    设幂级数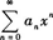在x=2处收敛，则该级数在x=-1处必定()．

    A.发散
    B.条件收敛
    C.绝对收敛
    D.敛散性不能确定

    答案：C
    解析：

  • 第20题：

    当n趋于无穷时，级数的一般项的极限为0，则级数（）。

    • A、肯定收敛
    • B、肯定发散
    • C、不一定收敛
    • D、收敛于0

    正确答案:C

  • 第21题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第22题：

    单选题
    当n趋于无穷时，级数的一般项的极限为0，则级数（）。
    A

    肯定收敛

    B

    肯定发散

    C

    不一定收敛

    D

    收敛于0


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    已知级数的收敛域为［-1，3），则级数的收敛域为（）．
    A

    ［-2，2）

    B

    ［-1，2）

    C

    （-1，2］

    D

    （-2，2］


    正确答案： A
    解析： 暂无解析

相关内容