将函数f(x）=1/(3-x)展开成(x+1)的幂级数并指出收敛区间（6分）

第1题：

幂级数在区间(-1，1)内的和函数S(x)=________.

答案：

解析：

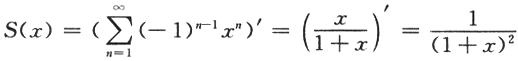
第2题：

函数1/x展开成(x-2)的幂级数为（ ）。

答案：A

解析：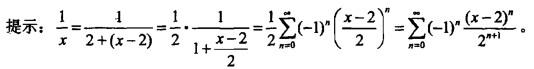

第3题：

下列结论正确的是：（） （1）幂级数在收敛区间内一定绝对收敛。 （2）经过计算求得幂级数的收敛半径为R，则R一定是正常数。 （3）幂级数在区间[-R,R]上连续。 （4）幂级数的和函数S（x)在收敛域上连续。 （5）幂级数在收敛域上逐项可微，可微后所得到幂级数与原级数具有相同的收敛域。 （6）幂级数的收敛区间就是我们俗称的收敛域。 （7）幂级数在收敛域上不可能条件收敛。 （8）幂级数在收敛区间内逐项可积，可积后所得到幂级数与原级数有相同的收敛区间。

A．（1）（8）

B．（1）（7）

C．（1）（3）（8）

D．（1）（3）（5）（8）

E．（1）（2）（8）

F．（2）（3）（5）

G．（5）（6）（8）

H．（4）（7）

I．全部正确

J．全部错误

第4题：

将函数f(x)=1-x(0≤x≤π)展开成余弦级数，并求级数的和.

答案：

解析：

第5题：

答案：

解析：