函数1/x展开成(x-2)的幂级数是:

题目

函数1/x展开成(x-2)的幂级数是:

相似考题

1.将函数f(x）=1/(3-x)展开成(x+1)的幂级数并指出收敛区间（6分）

3.下列给定程序中，函数fun()的功能是：计算S=f(-n)+f(-n+1)+…+f(0)+f(1)+f(2)+…f(n)的值。例如，当n为5时，函数值应为10.407143。f(x)函数定义如下：请改正程序中的错误，使它能得山正确的结果。注意：不要改动main 函数，不得增行或删行，也不得更改程序的结构。试题程序：include ＜conio. h＞include ＜stdio. h＞include ＜math. h＞/**************found***************/f (double x){if (x==0.0 ｜｜ x==2.0)return 0.0;else if (x＜0.0)return (x-1) / (x-2);elsereturn (x+1) / (x-2);}double fun(int n){int i; double s=0.0,y;for (i=-n; i＜=n; i++){ y=f(1.0*i); s+=y;}/**************found**************/return s}main(){ clrscr();printf ("%f\n", fun (5));}

4.将函数f(x）=x2e2x展开成x的幂级数。

参考答案和解析

答案：A

解析：

提示:将函数1/x变形后，再利用已知函数1/(x+1)的展开式写出结果。

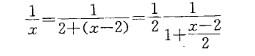
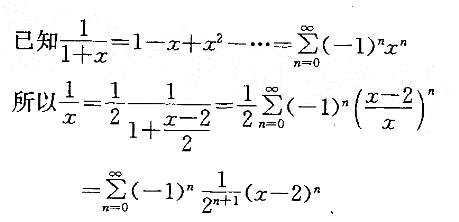
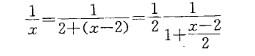
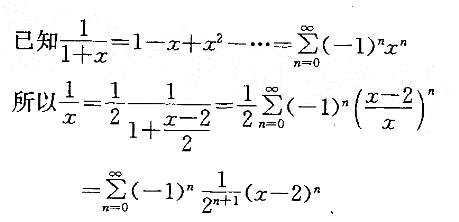
更多“函数1/x展开成(x-2)的幂级数是:”相关问题

第1题：

幂级数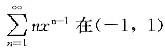内的和函数为( )。

答案：B
解析：
设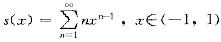由逐项积分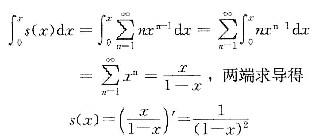
第2题：

函数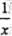展开成（x-2）的幂级数是：

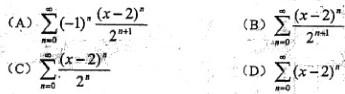答案：A
解析：
由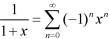得到启发，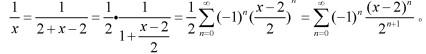
第3题：

幂级数在区间(-1，1)内的和函数S(x)=________.

答案：
解析：
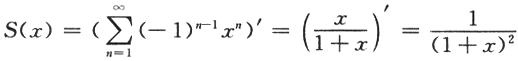
第4题：

设数列{an}满足条件：a0=3，a1=1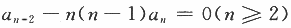，，S(x)是幂级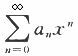数的和函数.
　　(Ⅰ)证明：S"(x)-S(x)=0；
　　(Ⅱ)求S(x)的表达式.

答案：
解析：
【分析】利用幂级数可逐项求导的性质，验证(Ⅰ)成立；解微分方程求出S(x)，注意初值条件的使用.
第5题：

函数1/x展开成(x-2)的幂级数是( )。

A.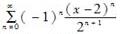
B.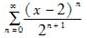
C.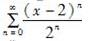
D.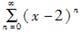

答案：A
解析：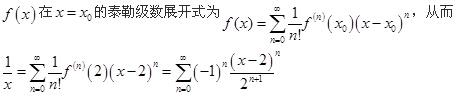
第6题：

A.（x+2）（2x-1）2
B.（x-2）（x+1）2
C.（2x+1）（x2-2）
D.（2x-1）（x+2）2
E.（2x+1）2（x-2）

答案：B
解析：
第7题：

函数1/x展开成(x-2)的幂级数为（）。

答案：A
解析：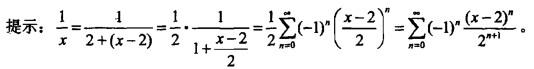
第8题：

函数f（x）=x／（x²-5x+6）展开成（x-5）的级数的收敛区间是（）
- A、（-1，1）
- B、（-1，1）
- C、（3，7）
- D、（4，5）
正确答案:C
第9题：

在数域F上x^2-3x+2可以分解成（）。
- A、（x-1）^2
- B、（x-1）（x-3）
- C、（x-2）（x-3）
- D、（x-1）（x-2）
正确答案:D
第10题：

设a<0，则当满足条件（）时，函数f（x）=ax3+3ax2+8为增函数。
- A、x<-2
- B、-2
- C、x>0
- D、x<-2或x>0
正确答案:B
第11题：

单选题
设函数f（x）＝x2（x－1）（x－2），则f′（x）的零点个数为（　　）。
A
0
B
1
C
2
D
3

正确答案： A
解析：
函数f（x）＝x²（x－1）（x－2），f（0）＝f（1）＝f（2）＝0，由罗尔定理可知，至少有ξ₁∈（0，1）、ξ₂∈（1，2）使得f′（ξ₁）＝0，f′（ξ₂）＝0，即f′（x）至少有两个零点。又函数f（x）是四次多项式，故f′（x）是三次多项式，三次方程f′（x）＝0的实根不是一个就是三个，故f′（x）有三个零点。
第12题：

单选题
（x^3-6x^2+11x-6，x^2-3x+2）=（）。
A
（x-1）（x+2）
B
（x+1）（x-2）
C
（x-1）（x-2）
D
（x-2）（x-3）

正确答案： C
解析：暂无解析
第13题：

函数ex展开成为x-1的幂函数是：

答案：B
解析：
提示:已知ex=e x- 1+1=e ? e x-1。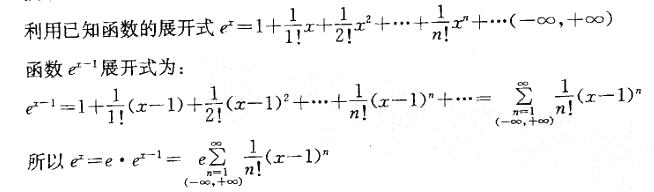
第14题：

不等式2(x-2)≤x-2的非负整数解的个数为().?

A.1
B.2
C.3
D.4

答案：C
解析：
解2(x-2)≤x-2得x≤2，故非负整数解为0，1，2，即有3个.
第15题：

将函数f(x)=1-x(0≤x≤π)展开成余弦级数，并求级数的和.

答案：
解析：
第16题：

幂级数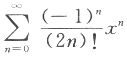在(0,+∞)内的和函数S(x)=_________.

答案：
解析：
利用余弦函数的幂级数展开式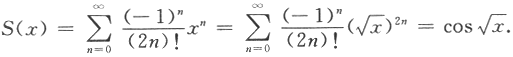
第17题：

设函数f(x－2)＝x2－3x－2，则f(x)＝（　　）

A.x2＋x－4
B.x2－x－4
C.x2＋x＋4
D.x2－x%－4

答案：A
解析：
第18题：

当∣x∣≤4时,函数y=∣x-1∣+∣x-2∣+∣x-3∣的最大值与最小值之差是

A.4
B.6
C.16
D.20
E.14

答案：C
解析：
第19题：

将函数f(x)=xe3x展开为x的幂级数，并指出其收敛区间．

答案：
解析：
第20题：

（x^3-6x^2+11x-6，x^2-3x+2）=（）。
- A、（x-1）（x+2）
- B、（x+1）（x-2）
- C、（x-1）（x-2）
- D、（x-2）（x-3）
正确答案:C
第21题：

MATLAB中提供的将函数展开为幂级数的函数是（）。
- A、taylor
- B、expand
- C、symsum
- D、float
正确答案:A
第22题：

单选题
函数f（x）=x／（x2-5x+6）展开成（x-5）的级数的收敛区间是（）
A
（-1，1）
B
（-1，1）
C
（3，7）
D
（4，5）

正确答案： B
解析：暂无解析
第23题：

单选题
在数域F上x^2-3x+2可以分解成（）。
A
（x-1）^2
B
（x-1）（x-3）
C
（x-2）（x-3）
D
（x-1）（x-2）

正确答案： D
解析：暂无解析

函数1/x展开成(x-2)的幂级数是:

题目

相似考题

参考答案和解析

更多“函数1/x展开成(x-2)的幂级数是:”相关问题

相关内容