设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。

题目

设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。

（1）求函数y=f(x)；

（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。

相似考题

1.设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

2.如果曲线y=f(x)在点（x,y）处的切线斜率与x2成正比，并且此曲线过点（1，-3）和（2，11），则此曲线方程为（ ）。A. y=x3-2B. y=2x3-5C. y=x2-2D. y=2x2-5

3.如果曲线Y=f(x）在点（x，y)处的切线斜率与x2成正比，并且此曲线过点(1，-3)和(2，11)，则此曲线方程为（　　）．A.Y=3-2 B.Y=2x3-5 C.Y=x2-2 D.Y=2x2-5

4.已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．（I）求a，b；（II）求f（x）的单调区间，并说明它在各区间的单调性．

更多“设曲线y=f(x)上任一点(x,y)处的切线斜率为(y／x)＋x2,且该曲线经过点(1,1／2)。 (1)求函数y ”相关问题

  • 第1题：

    求函数y=x-lnx的单调区间，并求该曲线在点(1，1)处的切线l的方程．


    答案：
    解析：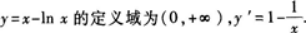


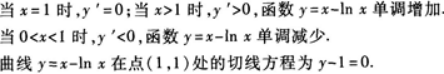
    【评析】求函数f(x)的单调区间，应先判定函数的定义域．求出函数的驻点，即y′=0的点；求出y的不可导的点，再找出y′>0时x的取值范围，这个范围可能是一个区间，也可能为几个区间．

  • 第2题：

    3、设方程y=sin（xy)+3确定了函数y=f（x),求曲线y=f（x)在点（0,3)处的切线斜率


    故

  • 第3题：

    一曲线经过原点，且曲线上任意一点（x,y）处的切线斜率为2x，则曲线方程为________。


    y=x^2

  • 第4题：

    2、一曲线过原点且在曲线上每一点（x,y)处的切线斜率等于x，求这曲线的方程


    解：设这曲线的方程为y=f（x）, ∵该曲线上任一点M(x,y)处的切线的斜率是y′=f′（x）, 此点与原点的连线的斜率是y/x.又它们互相垂直. ∴y′y/x=-1.解此微分方程得y2+x2=C,（C是积分常数） ∵此曲线通过点(1,1).∴当x=1时,y=1.代入（1）得C=2,则y2+x2=2.故这曲线的方程是y2+x2=2.

  • 第5题：

    一曲线经过原点，且曲线上任意一点（x,y）处的切线斜率为2x，则曲线方程为________。

    A．y=4x^2

    B．y=x^3

    C．y=x^2

    D．y=x^2+1


    B

相关内容