设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。A、0B、π/2C、锐角D、钝角

题目
设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。

A、0

B、π/2

C、锐角

D、钝角

相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.函数f(x)二阶可导,且f’(x0)=0,则点(x0,f(x0))为曲线y=f(x)的拐点。()此题为判断题(对，错)。

3.函数y=f(x)在点x=x0处取得极小值，则必有： A.f′(x0)=0 B.f′′(x0)＞0 C. f′(x0)=0 且 f(xo)＞0 D.f′(x0)=0 或导数不存在

4.曲线y=f(x)在点(x0,f(x0))有拐点,且f''(x0)存在,则f''(x0)=1。()此题为判断题(对，错)。

更多“设函数y=f(x)在点x0处可导,且f′(x)0,曲线y=f(x)则在点(x0,f(x0))处的切线的倾斜角为()。 ”相关问题

  • 第1题：

    函数y=f(x) 在点x=x0处取得极小值，则必有：
    A. f'(x0)=0
    B.f''(x0)＞0
    C. f'(x0)=0且f''(x0)＞0
    D.f'(x0)=0或导数不存在


    答案：D
    解析：
    提示：已知y=f(x)在x=x0处取得极小值，但在题中f(x)是否具有一阶、二阶导数，均未说明，从而答案A、B、C就不一定成立。答案D包含了在x=x0可导或不可导两种情况，如y= x 在x=0处导数不存在，但函数y= x 在x=0取得极小值。

  • 第2题：

    设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.


    答案：
    解析：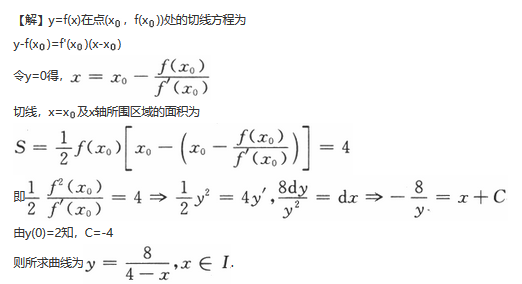

  • 第3题：

    函数y=f（x)在点x=x0 处取得极大值，则

    A．f′(x0) = 0.

    B．f′′(x0) ＜ 0.

    C．f′(x0) = 0 且 f′′(x0) ＜ 0.

    D．f′(x0) = 0 或不存在.


    A

  • 第4题：

    下列命题正确的是（）

    A.函数f(x)的导数不存在的点，一定不是f(x)的极值点
    B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点
    C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0
    D.若函数f(x)在点x0处连续，则f'(x0)一定存在

    答案：C
    解析：
    根据函数在点x0处取极值的必要条件的定理，可知选项C是正确的．

  • 第5题：

    函数y =f(x)在点x=x0处取得极小值，则必有（ ）。
    A. f'(x0)=0 B. f''(x0) > 0
    C.f'(x0) = 0且f''(x0)>0 D. f'(x0)=0或导数不存在


    答案：D
    解析：
    提示：极值在导数为零的点和导数不存在的点取到。

相关内容