若二次函数y=f（x）的图像过点（0，o），（-1，1）和（-2，o），则f（x）=__________.

题目

若二次函数y=f（x）的图像过点（0，o），（-1，1）和（-2，o），则f（x）=__________.

相似考题

1.以下结论正确的是()。A、若x0为函数y=f(x)的驻点,则x0必为函数y=f(x)的极值点.B、函数y=f(x)导数不存在的点,一定不是函数y=f(x)的极值点.C、若函数y=f(x)在x0处取得极值,且f′(x)存在,则必有f′(x)=0.D、若函数y=f(x)在x0处连续,则y=f′(x0)一定存在.

2.下列函数参数默认值定义错误的是( )。A．f(int x,int y=O)B．fun(int x=100)C．f(int x=0,int y)D．fun(int x=f())(函数f()已经定义)

3.下列命题正确的是（）A.函数f(x)的导数不存在的点，一定不是f(x)的极值点 B.若x0为函数f(x)的驻点，则x0必为f(x)的极值点 C.若函数f(x)在点x0处有极值，且f'(x0)存在，则必有f'(x0)＝0 D.若函数f(x)在点x0处连续，则f'(x0)一定存在

4.设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。

更多“若二次函数y=f（x）的图像过点（0，o），（-1，1）和（-2，o），则f（x）=__________.”相关问题

  • 第1题：

    已知函数f(x)=㏑(x+2)-x2+bx+c，
    (1)若点P(-1，0)在f(x)的图象上，过点P的切线与直线y=-x+2平行，求f(x)的解析式；
    (2)若f(x)在区间[0，2]上单调递增，求b的取值范围。


    答案：
    解析：

  • 第2题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第3题：

    若函数f(x)＝log2(5x＋1)，则其反函数y＝f－1(x)的图像过点（　　）

    A.(2，1)
    B.(3，2)
    C.(2，3)
    D.(4，3)

    答案：D
    解析：
    反函数与原函数的．27与y互换．把x＝3，y＝4代入，f(x)成立。 故反函数过点(4，3)．(答案为D)

  • 第4题：

    设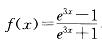，则：

    A.f(x)为偶函数，值域为(-1，1)
    B.f(x)为奇函数，值域为(-∞，0)
    C.f(x)为奇函数，值域为(-1，1)
    D.f(x)为奇函数，值域为(0，+∞)

    答案：C
    解析：

  • 第5题：

    设函数z=f（x，y）的全微分为dz=xdx+ydy，则点（0，0）（ ）《》（ ）

    A.不是f（x，y）的连续点
    B.不是f（x，y）的极值点
    C.是f（x，y）的极大值点
    D.是f（x，y）的极小值点

    答案：D
    解析：

  • 第6题：

    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.


    正确答案:错误

  • 第7题：

    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。

    • A、f（x，y）的极值点一定是f（x，y）的驻点
    • B、如果P0是f（x，y）的极值点，则P0点处B2-AC<0
    • C、如果P0是可微函数f（x，y）的极值点，则P0点处df=0
    • D、f（x，y）的最大值点一定是f（x，y）的极大值点

    正确答案:C

  • 第8题：

    单选题
    以下关于二元函数的连续性的说法正确是（　　）。
    A

    若f（x，y）沿任意直线y＝kx在点x＝0处连续，则f（x，y）在（0，0）点连续

    B

    若f（x，y）在点（x0，y0）点连续，则f（x0，y）在y0点连续，f（x，y0）在x0点连续

    C

    若f（x，y）在点（x0，y0）点处偏导数fx′（x0，y0）及fy′（x0，y0）存在，则f（x，y）在（x0，y0）处连续

    D

    以上说法都不对


    正确答案： D
    解析：
    根据二元函数f（x，y）在（x0，y0）出连续的定义可知B项正确。

  • 第9题：

    单选题
    y＝f（x）是方程y″－2y′＋4y＝0的一个解，若f（x0）＞0，f′（x0）＝0，则函数f（x）（　　）。
    A

    在x0点取得极大值

    B

    在x0的某邻域单调增加

    C

    在x0点取得极小值

    D

    在x0的某邻域单调减少


    正确答案： D
    解析：
    由f′（x0）＝0代入y″－2y′＋4y＝0可得y″（x0）＝－4y（x0）＜0。又f′（x0）＝0，故函数y＝f（x）在x0处取得极大值。

  • 第10题：

    填空题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

    正确答案： x-y=0
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第11题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    －x－y＝0

    B

    x－y－1＝0

    C

    x－y＝0

    D

    x＋y＝0


    正确答案： A
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第12题：

    单选题
    若函数f（x，y）在闭区域D上连续，下列关于极值点的陈述中正确的是（）。
    A

    f（x，y）的极值点一定是f（x，y）的驻点

    B

    如果P0是f（x，y）的极值点，则P0点处B2-AC<0

    C

    如果P0是可微函数f（x，y）的极值点，则P0点处df=0

    D

    f（x，y）的最大值点一定是f（x，y）的极大值点


    正确答案： C
    解析： 暂无解析

  • 第13题：

    已知二次函数f(x)的二次项系数为实数a，且其图像与直线2x+y=0交点横坐标为1和3．
    (1)若方程f(x)+6a=0有两个相等的实数根，求f(x)的解析式；
    (2)若f(x)的最大值为正数，求实数n的取值范围．


    答案：
    解析：
    解：根据题意f(x)与2x+y=0的交点为(1，-2)、(3，-6)，设f(x)=ax2+bx+c，将上述两个交点代入，有a+b+c=-2，9a+36+c=-6，整理可得b=-2-4a，c=3a.

  • 第14题：

    若函数z=f（x，y）在点P0（x0，y0）处可微，则下面结论中错误的是（　　）。



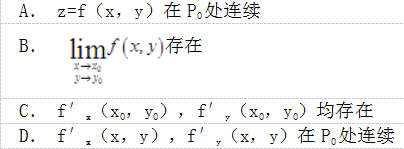    答案：D
    解析：
    二元函数z=f（x，y）在点（x0，y0）处可微，可得到如下结论：①函数在点（x0，y0）处的偏导数一定存在，C项正确；②函数在点（x0，y0）处一定连续，AB两项正确；可微，可推出一阶偏导存在，但一阶偏导存在不一定一阶偏导在P0点连续，也有可能是可去或跳跃间断点，故D项错误。

  • 第15题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是：

    A.f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC
    C.如果P0是可微函数f(x,y)的极值点，则在P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点

    答案：C
    解析：
    提示 在题目中只给出f(x,y)在闭区域D上连续这一条件，并未讲函数f(x,y)在P0点是否具有一阶、二阶偏导，而选项A、B判定中均利用了这个未给的条件，因而选项A、B不成立。选项D中f(x,y)的最大值点可以在D的边界曲线上取得，因而不一定是f(x,y)的极大值点，故选项D不成立。
    在选项C中，给出p0是可微函数的极值点这个条件，因而f(x,y)在P0偏导存在，且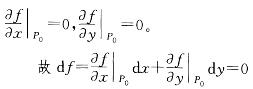

  • 第16题：

    若函数f(x,y)在闭区域D上连续，下列关于极值点的陈述中正确的是（ ）。
    A. f(x,y)的极值点一定是f(x,y)的驻点
    B.如果P0是f(x,y)的极值点，则P0点处B2-AC)
    C.如果P0是可微函数f(x,y)的极值点，则P0点处df=0
    D.f(x,y)的最大值点一定是f(x,y)的极大值点


    答案：C
    解析：
    提示：如果P0是可微函数f(x,y)的极值点，由极值存在必要条件，在P0点处有

  • 第17题：

    设函数f（x，y）＝x3+y3-3xy，则（）。

    • A、f（0，0）为极大值
    • B、f（0，0）为极小值
    • C、f（1，1）为极大值
    • D、f（1，1）为极小值

    正确答案:D

  • 第18题：

    设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）>O，f’（x0）=0，则函数f（x）在点x0（）．

    • A、取得极大值
    • B、取得极小值
    • C、的某个邻域内单调增加
    • D、的某个邻域内单调减少

    正确答案:A

  • 第19题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第20题：

    单选题
    设函数f（x）满足关系式f″（x）＋[f′（x）]2＝x，且f′（0）＝0，则（　　）。
    A

    f（0）是f（x）的极大值

    B

    f（0）是f（x）的极小值

    C

    点（0，f（0））是曲线y＝f（x）的拐点

    D

    f（0）不是f（x）的极值，点（0，f（0））也不是曲线y＝f（x）的拐点


    正确答案： C
    解析：
    已知f″（x）＋[f′（x）]2＝x，方程两边对x求导得f‴（x）＋2f″（x）·f′（x）＝1，由f′（0）＝0，则f″（0）＝0，f‴（0）＝1，故在点x＝0的某邻域内f″（x）单调增加，即f－″（0）与f＋″（0）符号相反，故点（0，f（0））是曲线y＝f（x）的拐点。

  • 第21题：

    判断题
    若连续函数y=f（x）在x0点不可导，则曲线y=f(x)在（x0,f(x0））点没有切线.
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第22题：

    单选题
    设y=f（x）是微分方程y"-2y’+4y=0的一个解，又f（x0）>O，f’（x0）=0，则函数f（x）在点x0（）．
    A

    取得极大值

    B

    取得极小值

    C

    的某个邻域内单调增加

    D

    的某个邻域内单调减少


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

相关内容