设空间有一点p，则p到平面（n，d）的最短距离为（）A、n.p+dB、dC、n.pD、无法计算

题目

设空间有一点p，则p到平面（n，d）的最短距离为（）

A、n.p+d
B、d
C、n.p
D、无法计算

相似考题

1.设X～N(0，1)，则下列各式成立的有( )。A．P(X＞a)=P(X≥a)=1-Ф(a)B．P(a≤X≤b)=Ф(b)-Ф(a)C．P(｜X｜≤a)=2Ф(a)-1D．Ф(-a)=-Ф(a)E．P(X＜a)=P(X≥a)=1-Ф(a)

2.设p0是静止液体液面上的外加压力,h是液体内任一点A距液面的高度,则A点的压力p为()。A..p=p0+ρghB.p=p0-ρghC.p=ρghD.p=-ρgh

3.设数值变量N的值为1或2，若为1，则执行程序P1．PRG，若为2，则执行程序P2．PRG，以下错误的程序段是( )。A．DO CASE CASE N=1 DO P1 CASE N-2 DO P2 ENDCASEB．IF N=1 DO P1 ELSE DO P2 ENDIFC．N=”P”+N DOAC1D．C1=STR(N，1) DO P&C1

4.设P是图G从vs到vt的最短路，则有A、P的长度等于P的每条边的长度之和B、P的最短路长等于vs到vt的最大流量C、P的长度等于G的每条边的长度之和D、P有n个点n-1条边

参考答案和解析

正确答案:A

更多“设空间有一点p，则p到平面（n，d）的最短距离为（）”相关问题

第1题：

正态分布计算所依据的重要性质为( )。
A．设X～N(μ,σ2)，则u=(X-μ)/σ～N(0，1)
B．设X～N(μ，σ2)，则对任意实数a、b有P(X＜b)=Ф[(b-μ)/σ)
C．设X～N(μ，σ2)，则对任意实数a、b有P(X＞a)=1-Ф[(a-μ)/σ]
D．设X～N(μ，σ2)，则对任意实数a、b有P(a＜X＜b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]
E．设X～μ(μ1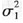，，Y～N(μ2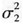，，则X+Y～N(μ1+μ2，(σ1+σ2) 2)

正确答案：ABCD
解析：若X～N(μ1，)，Y-N(μ2，)，X与Y相互独立，则(X+Y)～N(μ1，+μ2，+)。
第2题：

设X～N（μ,4^2）,y～N(μ,5^2),令p=P(X≤μ一4),q=P(Y≥μ+5),则().

A.p>q
B.pC.p=q
D.p,q的大小由μ的取值确定

答案：C
解析：
由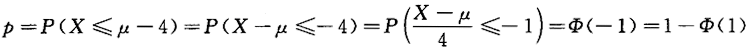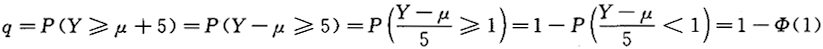，，得p=q，选(C).
第3题：

设X~N(0，1)，则下列各式成立的有（）。
A. P(X>a)=P(X≥a) =1 -Φ(a) B. P(a≤X≤b) =Φ(b) -Φ(a)
C. P( X ≤a) =2Φ(a) -1 D. Φ(-a) = -Φ(a)
E. P(X

答案：A,B,C
解析：
对于标准正态分布有Φ(-a) =1 -Φ(a), P(X
第4题：

设X～N（2,σ^2）,且P(2≤X≤4)=0.4,则P(X<0)=_______.

答案：1、0.1
解析：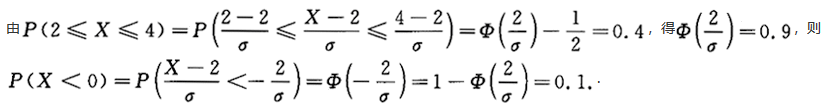
第5题：

设本金为P，利率为i，本利和为F，计息期数为n，每年末投资为A（在几年内），则现值系数可表示为（　　）。
A．P（1+i）n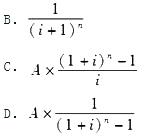

答案：B
解析：
现值是指按规定的贴现率，同某一时间的资金额等值的任何较早时间的资金额。已知终值F，求现值P，可表示为：（P/F，i，n），由公式F=P（1+i）n得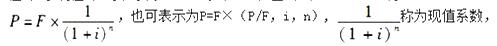：，用PW表示。
第6题：

抛物线x2=-16y上一点P到焦点的距离是6，则点P的坐标是( )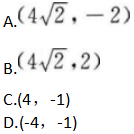

答案：A
解析：
【考情点拨】本题主要考查的知识点为抛物线的定义．【应试指导】本题应从抛物线的定义去考虑．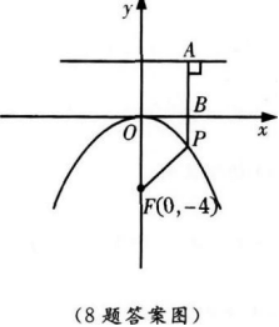

∴F(0，-4)，
∴准线方程y=4，由题意得｜PF｜=6，
∴｜PA｜=6，
∵｜AB｜=4，
∴｜PB｜=2，
∴P点的坐标为(x，-2)，
∵P(x，-2)点在抛物线上，
∴x2=-16×(-2)=32．
第7题：

设M、N为随机事件，P(N)>0，且条件概率P(M|N)=1，则必有

答案：C
解析：
P(MUN)=P(M)+P(N)-P(MN)，P(MUN)=P(M)。
第8题：

有定义：int a[10]， n， *p1=a，*p2=&a[9]；，则正确的赋值语句为（）。
- A、n=p2-p1；
- B、n=p2*p1；
- C、n=p2+p1；
- D、n=p1/p2；
正确答案:A
第9题：

设随机变量X～N（2，9），且P{Xa}=P{Xa}，则a＝（）。

正确答案:2
第10题：

设某项即付年金的期金额为A，折现率为i，计息期数为n，则此即付年金的终值Vn的正确计算公式有（）。
- A、V_n=A（F/A i，n）
- B、V_n=A（P/A i，n）
- C、V_n=A（F/A i，n）（1=i）
- D、V_n=A[（F/A i，n=1）-1]
- E、V_n=A（P/A i，n）（P/F i，n）
正确答案:C,D
第11题：

设某项先付年金的期金额为A，必要的报酬率为i，计息期数为n，则该项先付年金的现值V₀的正确计算公式有（）
- A、V₀=A（P/Ai，n）
- B、V₀=A（F/Ai，n）
- C、V₀=A（P/Ai，n）（1+i）
- D、V₀=A[（P/Ai，n-1）+1]
- E、V₀=A（P/Ai，n）（P/Fi，n）
正确答案:C,D
第12题：

多选题
已知从第0年到第n年，每年年值为A，利率为i，期限为n，则现值P为（）。
A
A+A（P／A，i，n）
B
A（P／A，i，n+1）
C
A（P／A，i，n+1）（F／P，i，1）
D
A（F／A，i，n+1）（P／F，i，n）
E
A（F／A，i，n）（P／F，i，n）

正确答案： D,A
解析：暂无解析
第13题：

设随机变量X～b(n，P)，则下列关系式正确的有( )。

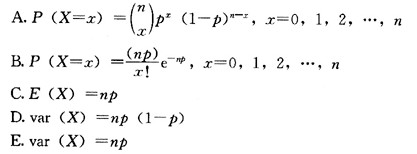正确答案：ACD
解析：由二项分布的性质可知。
第14题：

设随机变量X?N(0，σ2)，则对于任何实数λ都有:
(A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
(C) X-λ~N(λ，σ2-λ2)(D)λX~N(0，λσ2)

答案：B
解析：
解:选B。
排除错误选项。
X-λ~N(-λ，σ2)，选项C错误。
λX~N(0，λ2σ2)，选项D错误。
第15题：

正态分布计算所依据的重要性质为（）。
A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)
B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]
D.设X~N(μ,σ2),则对任意实数a、b有P(a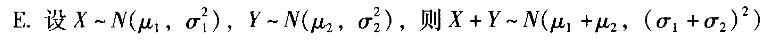

答案：A,B,C,D
解析：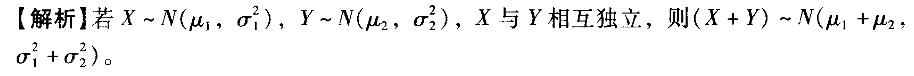
第16题：

设随机变量X～B（n,p）,且E(X)=5,E(X^2)=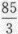,则n=_______,p=_______.

答案：
解析：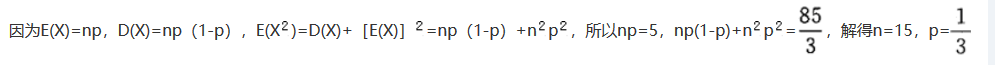
第17题：

已知正圆锥的底面半径是1cm，母线为3cm，P为底面圆周上一点，由P绕过圆锥回到P点的最短路径如图所示，由顶点V到这条路线的最小距离是多少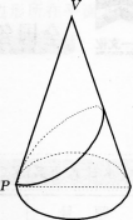

答案：
解析：
圆锥的曲面沿着母线剪开，展开成一个平面(如下图)，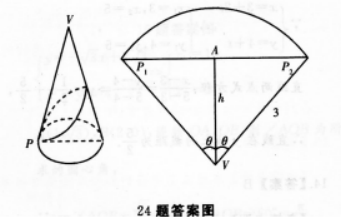

其半径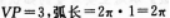的扇形
短距离，就是弦PlP2，由V到这条路线的最短距离是图中的线段h=AV．依据弧长公式2π=2θ·3，得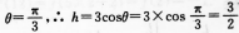
第18题：

如图4所示，半径为b的圆环状导线均匀带电，在垂直于环平面的轴线上有两点Pl和P2，Pl、P2到环心的距离分别为b和2b；设无限远处电势为零，P1、P2的电势分别为φ1，和φ2，则φ1/φ2为（）。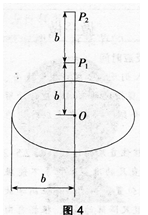

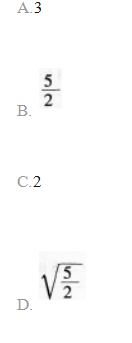答案：D
解析：
第19题：

在三维空间中，可用下面的哪个表达式表示平面（）。
- A、n.p+d=0，其中n为法线，p为平面上一点，d为常数
- B、n.P-d=0，其中n为法线，p为平面上一点，d为常数
- C、n×P=0，其中n为法线，p为平面上一点
- D、n×P+d=0，其中n为法线，p为平面上一点，d为常数
正确答案:A
第20题：

设年利率为i，现存入p元，不计复利，n年后可得钱数为（）
- A、p*（1+i﹡n）
- B、p*（i+1）n
- C、P*(1+n*i)
- D、p*（i+n）
正确答案:C
第21题：

设X服从二项分布，EX=2.4，DX=1.44，则二项分布的参数为（）.
- A、n=6，p=0.4
- B、n=6，p=0.1
- C、n=8，p=0.3
- D、n=24，p=0.1
正确答案:A
第22题：

设x1，…，X是取自总体X的容量为n的样本．已知总体X服从参数为p的二点分布，则等于（）．
- A、np（p）
- B、（n-1）p（p）
- C、np
- D、np2
正确答案:B
第23题：

单选题
设P是图G从vs到vt的最短路，则有（）
A
P的长度等于P的每条边的长度之和
B
P的最短路长等于v_s到v_t的最大流量
C
P的长度等于G的每条边的长度之和
D
P有n个点n-1条边

正确答案： A
解析：暂无解析

设空间有一点p，则p到平面（n，d）的最短距离为（）A、n.p+dB、dC、n.pD、无法计算

题目

相似考题

参考答案和解析

更多“设空间有一点p，则p到平面（n，d）的最短距离为（）”相关问题

相关内容