函数在区间上的极大值一定大于极小值。
题目
函数在区间上的极大值一定大于极小值。
相似考题
参考答案和解析
错误
更多“函数在区间上的极大值一定大于极小值。”相关问题
-
第1题：
最佳值是()A、极大值
B、极小值
C、既不是极大值，也不是极小值
D、能是极大值，也可能是极小值
正确答案：D
-
第2题：
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点答案：C解析：根据导函数的图形可知，一阶导数为零的点有3个，而x＝0是导数不存在的点。三个一阶导数为零的点左右两侧导数符号不一致，必为极值点，且两个极小值点，一个极大值点；在x=0左侧一阶导数为正，右侧一阶导数为负，可见x=0为极大值点，故f(x)共有两个极小值点和两个极大值点。 -
第3题：
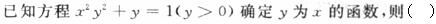A.y（x）有极小值，但无极大值
B.y（x）有极大值，但无极小值
C.y（x）既有极大值又有极小值
D.无极值答案：B解析：
-
第4题：
f（x）在（－∞，＋∞）内连续，其导数函数f′（x）图形如图所示，则f（x）有（ ）。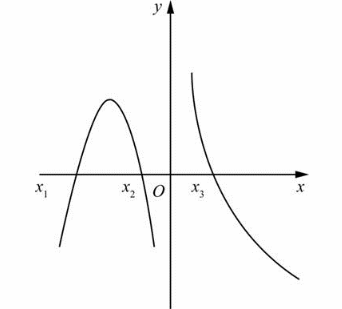
A．一个极小值点和两个极大值点
B．两个极小值点和两个极大值点
C．两个极小值点和一个极大值点
D．一个极小值点和三个极大值点答案：B解析：由导函数f ′（x）图像可知，函数f（x）有三个驻点x1、x2、x3和一个导数不存在的点0。根据题6解表，原函数f（x）在x1和0处取得极小值，在x2和x3处取得极大值。因此，f（x）有两个极小值点和两个极大值点。
题6解表 函数单调区间表
-
第5题：
设函数(x)在x=0处连续，当x<0时，'(x)<0；当x>0时，，(x)>0．则()．A.(0)是极小值
B.(0)是极大值
C.(0)不是极值
D.(0)既是极大值又是极小值答案：A解析：根据极值的第一充分条件可知A正确． -
第6题：
关于函数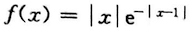
的极值个数，正确的是A. 有2个极大值，1个极小值
B. 有1个极大值，2个极小值
C. 有2个极大值，没有极小值
D. 没有极大值，有2个极小值答案：A解析：
-
第7题：
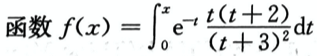A. 有1个极小值，1个极大值，1条渐近线
B.有1个极小值，1个极大值，2条渐近线
C.有2个极小值，1个极大值，1条渐近线
D.有2个极小值，2个极大值，2条渐近线答案：B解析：
-
第8题：
设函数f(x)=(1+x)ex，则函数f(x)（ ）A.有极小值
B.有极大值
C.既有极小值又有极大值
D.无极值答案：A解析：【考情点拨】本题考查了函数极值的知识点.【应试指导】
-
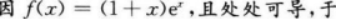
第9题：
设函数f（x，y）＝x3+y3-3xy，则（）。
- A、f（0，0）为极大值
- B、f（0，0）为极小值
- C、f（1，1）为极大值
- D、f（1，1）为极小值
正确答案:D -
第10题：
最优化控制就是在一定的约束条件下,选择一个表征过程的控制函数,再确定一个最佳的目标函数,以使目标函数取极大值或极小值
正确答案:错误 -
第11题：
判断题最优化控制就是在一定的约束条件下,选择一个表征过程的控制函数,再确定一个最佳的目标函数,以使目标函数取极大值或极小值A对
B错
正确答案： 错解析： 暂无解析 -
第12题：
单选题已知方程x2y2＋y＝1（y＞0）确定y为x的函数，则（ ）。Ay（x）有极小值，但无极大值
By（x）有极大值，但无极小值
Cy（x）既有极大值又有极小值
D无极值
正确答案： C解析：
方程x2y2＋y＝1（y＞0），两边对x求导得2xy2＋2x2y·y′＋y′＝0。y′＝0时，x＝0（y＞0）。再次求导得2y2＋4xy·y′＋4xy·y′＋2x2·（y′）2＋2x2y·y″＋y″＝0。故x＝0时，y＝1，y′（0）＝0，y″（0）＝－2＜0，则函数在x＝0点取得极大值，又因函数只有一个驻点，所以函数无极小值。 -
第13题：
设两函数f(x)及g(x)都在x=a处取得极大值，则函数F(x)=f(x)g(x)在x=a处( )。A.必取极大值
B.必取极小值
C.不可能取极值
D.是否取极值不能确定答案：D解析：
-
第14题：
设f（x）=xsinx+cosx，则下列命题中正确的是（ ）。A.f（0）是极大值，f（π/2）是极小值
B.f（0）是极小值，f（π/2）是极大值
C.f（0）是极大值，f（π/2）也是极大值
D.f（0）是极小值，f（π/2）也是极小值。答案：B解析：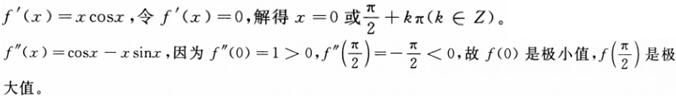
-
第15题：
设函数f(x)在
内连续，其导函数的图形如图所示，则f(x)有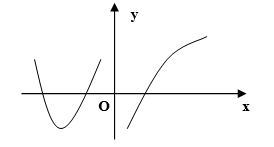 
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点答案：C解析：
-
第16题：
设函数(x)=ax3+bx2+x在x=1处取得极大值5．
①求常数a和b；
②求函数(x)的极小值．答案：解析：①'(x)=3ax2+2bx+1．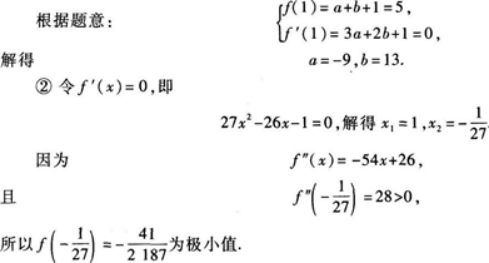
-
第17题：
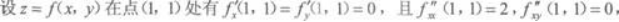
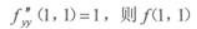A.是极大值
B.是极小值
C.不是极大值
D.不是极小值答案：B解析：根据极值的充分条件：B2－AC＝－2，A＝2＞0所以f(1，1)为极小值，选B． -
第18题：
设函数y-f(x)连续，除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下，则y=f(x)
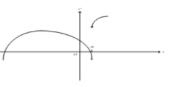A.有两个极大值点，一个极小值点，一个拐点
B.有一个极大值点，一个极小值点，两个拐点
C.有一个极大值点，一个极小值点，一个拐点
D.有一个极大值点，两个极小值点，两个拐点答案：D解析：
-
第19题：
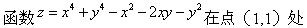A.极大值为2
B.极小值为－2
C.极小值为2
D.极大值为－2答案：B解析： -
第20题：
求函数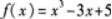
的极大值与极小值．答案：解析：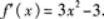
-
第21题：
在吸收光谱曲线中，吸光度的最大值是偶数阶导数光谱曲线的（）
- A、极大值
- B、极小值
- C、零
- D、极大值或极小值
正确答案:D -
第22题：
单选题设f（x）＝xsinx＋cosx。下列命题中正确的是（ ）。Af（0）是极大值，f（π/2）是极小值
Bf（0）是极小值，f（π/2）是极大值
Cf（0）是极大值，f（π/2）也是极大值
Df（0）是极小值，f（π/2）也是极小值
正确答案： B解析：
由f（x）＝xsinx＋cosx得
f′（x）＝sinx＋xcosx－sinx＝xcosx
f″（x）＝cosx－xsinx
又f′（0）＝f′（π/2）＝0，f″（0）＞0，f″（π/2）＜0，故f（0）是极小值，f（π/2）是极大值。 -
第23题：
单选题若f（x）和g（x）在x＝x0处都取得极小值，则函数F（x）＝f（x）＋g（x）在x＝x0处（ ）A必取得极小值
B必取得极大值
C不可能取得极值
D可能取极大值，也可能去极小值
正确答案： A解析：
根据极值的定义可知
∃δ1＞0使x∈（x0－δ1，x0＋δ1）时，f（x）＞f（x0）；
∃δ2＞0使x∈（x0－δ2，x0＋δ2）时，g（x）＞g（x0）；
取δ＝min[δ1，δ2]，则x∈（x0－δ，x0＋δ）时，有f（x）＋g（x）＞f（x0）＋g（x0），即F（x）＝f（x）＋g（x）在x＝x0处取得极小值。 -
第24题：
单选题设两函数f（x）及g（x）都在x＝a处取得极大值，则F（x）＝f（x）g（x）在x＝a处（ ）A必取极大值
B必取极小值
C不可能取极值
D是否取得极值不能确定
正确答案： D解析：
本题采用举例法进行排除较为简单。
令f（x）＝g（x）＝－|x|，f（x）与g（x）都在x＝0处取得极大值，但是f（x）g（x）＝x2在x＝0处取到极小值，故A、C项错误；
令f（x）＝1－x2，g（x）＝－x2，则f（x）与g（x）都在x＝0处取得极大值，分别是1和0，f（x）g（x）＝x4－x2在x＝0处取得极大值0，故B项错误。