假设A公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。6个月以后股价有两种可能,即上升33.33%,或者下降25%,无风险报酬率为每年4%。 要求:(1)根据套期保值原理估计期权价值。 要求:(2)如果期权市场上,每份看涨期权的价格为6.7元,是否存在套利的可能性,如果存在,应该如何套利?
题目
假设A公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。6个月以后股价有两种可能,即上升33.33%,或者下降25%,无风险报酬率为每年4%。
要求:(1)根据套期保值原理估计期权价值。
要求:(2)如果期权市场上,每份看涨期权的价格为6.7元,是否存在套利的可能性,如果存在,应该如何套利?
要求:(1)根据套期保值原理估计期权价值。
要求:(2)如果期权市场上,每份看涨期权的价格为6.7元,是否存在套利的可能性,如果存在,应该如何套利?
相似考题
参考答案和解析
答案:
解析:
1.(1)计算6个月后股票价格:
Su=So×u=50×(1+33.33%)=66.67(元)
Sd=So×d=50×(1-25%)=37.5(元)
(2)计算6个月后多头看涨期权价值:
Cu=So-X==66.67-52.08=14.59(元)
Cd=0
(3)计算套期保值比率
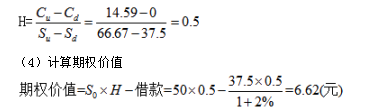
2.期权价值(6.62元)与期权市场的期权价格(6.7元)不相等,存在套利空间。
套利方法:出售1股看涨期权(6.7元),借款18.38元[=37.5×0.5/(1+2%)],购买0.5股股票支出25元(=50×0.5),可获利0.08元(6.7-6.62)。
Su=So×u=50×(1+33.33%)=66.67(元)
Sd=So×d=50×(1-25%)=37.5(元)
(2)计算6个月后多头看涨期权价值:
Cu=So-X==66.67-52.08=14.59(元)
Cd=0
(3)计算套期保值比率
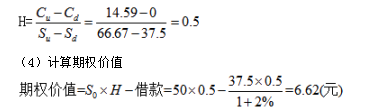
2.期权价值(6.62元)与期权市场的期权价格(6.7元)不相等,存在套利空间。
套利方法:出售1股看涨期权(6.7元),借款18.38元[=37.5×0.5/(1+2%)],购买0.5股股票支出25元(=50×0.5),可获利0.08元(6.7-6.62)。
更多“假设A公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权,执行价格为52.08元,到期时间是6个月。6个月以后股价有两种可能,即上升33.33%,或者下降25%,无风险报酬率为每年4%。 ”相关问题
-
第1题:
假设C公司股票现在的市价为20元,有1股以该股票为标的资产的看涨期权,执行价格为15元,到期时间是6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险报酬率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。
<1>、确定可能的到期日股票价格;
<2>、根据执行价格计算确定期权到期日价值;
<3>、计算套期保值比率;
<4>、计算购进股票的数量和借款数额;
<5>、根据上述计算结果计算期权价值;
<6>、根据风险中性原理计算期权的现值(假设股票不派发红利)。答案:解析:上行股价=20×(1+25%)=25(元)(0.5分)
下行股价=20×(1-20%)=16(元)(0.5分)
【考点“复制原理”】
股价上行时期权到期日价值=25-15=10(元)(0.5分)
股价下行时期权到期日价值=16-15=1(元)(0.5分)
【考点“复制原理”】
套期保值比率=(10-1)/(25-16)=1
【考点“复制原理”】
购进股票的数量=套期保值比率=1(股)(1分)
借款数额=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+6%×6/12)
=(16×1-1)/(1+3%)=14.56(元)(1分)
【考点“复制原理”】
期权价值=购买股票支出-借款=1×20-14.56=5.44(元)
【考点“复制原理”】
6%/2=上行概率×25%+(1-上行概率)×(-20%)
3%=0.45×上行概率-0.2
解得:上行概率=0.5111
下行概率=1-0.5111=0.4889(1分)
期权6个月后的期望价值
=0.5111×10+0.4889×1=5.60(元)
期权的现值=5.60/(1+3%)=5.44(元)(1分)
【思路点拨】在建立对冲组合时:
股价下行时期权到期日价值
=股价下行时到期日股票出售收入-偿还的借款本利和
=到期日下行股价×套期保值比率-借款本金×(1+r)
由此可知:
借款本金=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r)
【考点“复制原理”】 -
第2题:
假设甲公司的股票现在的市价为20元。有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。1年以后股价有两种可能:上升40%,或者降低30%。无风险利率为每年4%。
要求:利用单期二叉树定价模型确定期权的价值。答案:解析:期权价格=(1+r-d)/(u-d)×Cu/(1+r)=(1+4%-0.7)/(1.4-0.7)×7/(1+4%)=3.27(元) -
第3题:
某公司股票目前的市价为40元,有1份以该股票为标的资产的欧式看涨期权(1份期权包含1股标的股票),执行价格为42元,到期时间为6个月。6个月以后股价有两种可能:上升20%或者下降25%,则套期保值比率为( )。A.0.33
B.0.26
C.0.42
D.0.28答案:A解析:上行股价=40×(1+20%)=48(元),下行股价=40×(1-25%)=30(元);股价上行时期权到期日价值=48-42=6(元),股价下行时期权到期日价值=0;套期保值比率=(6-0)/(48-30)=0.33。 -
第4题:
假设ABC公司的股票现在的市价为80元。有1股以该股票为标的资产的看涨期权,执行价格为85元,到期时间6个月。6个月以后股价有两种可能:上升33.33%,或者降低25%。无风险利率为每年4%。现拟建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得6个月后该组合的价值与看涨期权相等。则下列计算结果正确的有( )。A.在该组合中,购进股票的数量0.4643股
B.在该组合中,借款的数量为27.31元
C.看涨期权的价值为9.834元
D.购买股票的支出为37.144元答案:A,B,C,D解析:上行股价=股票现价×上行乘数=80×1.3333=106.664(元)
下行股价=股票现价×下行乘数=80×0.75=60(元)
股价上行时期权到期日价值=上行股价-执行价格=106.664-85=21.664(元)
股价下行时期权到期日价值=0
套期保值比率H=期权价值变化量/股价变化量=(21.664-0)/(106.664-60)=0.4643
购买股票支出=套期保值比率×股票现价=0.4643×80=37.144(元)
借款=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r)=(60×0.4643)/(1+2%)=27.31(元)
期权价值=37.144-27.31=9.834(元) -
第5题:
假设ABC 公司的股票现在的市价为80 元。有1 股以该股票为标的资产的看涨期权,执行价格为85 元,到期时间6 个月。6 个月以后股价有两种可能:上升33.33%,或者降低25%。无风险报酬率为每年4%。则使用套期保值原理估算出该看涨期权价值为( )元。A.21.664
B.37.144
C.27.31
D.9.834答案:D解析:上行股价=股票现价×上行乘数=80×1.3333=106.664(元)下行股价=股票现价×下行乘数=80×0.75=60(元)股价上行时期权到期日价值=上行股价-执行价格=106.664-85=21.664(元)股价下行时期权到期日价值=0套期保值比率H=期权价值变化量/股价变化量=(21.664-0)/(106.664-60)=0.4643购买股票支出=套期保值比率×股票现价=0.4643×80=37.144(元)借款=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r)=(60×0.4643)/(1+2%)=27.31(元)期权价值=37.144-27.31=9.834(元)。 -
第6题:
ABC公司的股票目前的股价为10元,有1股以该股票为标的资产的欧式看涨期权,执行价格为10元,期权价格为2元,到期时间为6个月。假设年无风险利率为4%,计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格;
正确答案:看跌期权价格=看涨期权价格-标的资产价格+执行价格现值=2-10+10/(1+2%)=1.80(元) -
第7题:
假设甲公司的股票现在的市价为20元。有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。1年以后股价有两种可能:上升40%,或者下降30%。无风险报酬率为每年4%。拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合1年后的价值与购进该看涨期权相等。 要求: 期权的价值为多少?
正确答案: 期权价值=投资组合成本=购买股票支出一借款=0.5×20-6.73=3.27(元) -
第8题:
问答题假设甲公司的股票现在的市价为20元。有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。1年以后股价有两种可能:上升40%,或者降低30%。无风险利率为每年4%。要求:利用单期二叉树定价模型确定期权的价值。正确答案: 期权价格=(1+r-d)/(u-d)×Cu/(1+r)=(1+4%-0.7)/(1.4-0.7)×7/(1+4%)=3.27(元)解析: 暂无解析 -
第9题:
问答题计算分析题:假设C公司股票现在的市价为20元,有1股以该股票为标的资产的看涨期权,执行价格为15元,到期时间为6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年6%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。要求:(1)确定可能的到期日股票价格;(2)根据执行价格计算确定期权到期日价值;(3)计算套期保值比率;(4)计算购进股票的数量和借款数额;(5)根据上述计算结果计算期权价值;(6)根据风险中性原理计算期权的现值(假设期权期限内标的股票不派发红利)。正确答案: (1)上行股价=20×(1+25%)=25(元)下行股价=20×(1-20%)=16(元)(2)股价上行时期权到期日价值=25-15=10(元)股价下行时期权到期日价值=16-15=1(元)(3)套期保值比率=(10-1)/(25-16)=1(4)购进股票的数量=套期保值比率-1(股)借款数额=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+6%×6/,12)=(16×1-1)/(1+3%)=14.56(元)(5)期权价值=购买股票支出-借款=1×20-14.56=5.44(元)(6)6%/2=上行概率×25%+(1-上行概率)×(-20%)3%=0.45×上行概率-0.2解得:上行概率=0.5111下行概率=1-0.5111=0.4889期权6个月后的期望价值=0.5111×10+0.4889×1=5.60(元)期权的现值=5.60/(1+3%)=5.44(元)解析: 在建立对冲组合时:股价下行时期权到期日价值=股价下行时到期日股票出售收入-偿还的借款本利和=到期日下行股价×套期保值比率-借款本金×(1+r)由此可知:借款本金=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r) -
第10题:
多选题假设ABC公司的股票现在的市价为80元。有1股以该股票为标的资产的看涨期权,执行价格为85元,到期时间6个月。6个月以后股价有两种可能:上升33.33%,或者降低25%。无风险报酬率为每年4%。现拟建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得6个月后该组合的价值与看涨期权相等。则下列计算结果正确的有()。A在该组合中,购进股票的数量0.4643股
B在该组合中,借款的数量为27.31元
C看涨期权的价值为9.834元
D购买股票的支出为37.144元
正确答案: A,C解析: -
第11题:
单选题假设ABC公司的股票现在的市价为56.26元。有1股以该股票为标的资产的看涨期权,执行价格为62元,到期时间是6个月。6个月以后股价有两种可能:上升42.21%,或者下降29.68%。无风险利率为每年4%,则利用风险中性原理所确定的期权价值为()元。A7.78
B5.93
C6.26
D4.37
正确答案: A解析: 上行股价=56.26×(1+42.21%)=80.01(元)
下行股价=56.26×(1-29.68%)=39.56(元)
股价上行时期权到期日价值Cu=上行股价-执行价格=80.01-62=18.01(元)
股价下行时期权到期日价值Cd=0期望报酬率=2%=上行概率×42.21%+下行概率×(-29.68%)
2%=上行概率×42.21%+(1-上行概率)×(-29.68%)
上行概率=0.4407
下行概率=1-0.4407=0.5593
期权6个月后的期望价值=0.4407×18.01+0.5593×0=7.9370(元)
期权的价值=7.9370/(1+2%)=7.78(元) -
第12题:
问答题假设ABC公司的股票现在的市价为30元。有1份以该股票为标的资产的看涨期权,执行价格为30.5元,到期时间是6个月。6个月以后股价有两种可能:上升35%,或者下降20%。无风险利率为每年4%。拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合6个月后的价值与购进该看涨期权相等。计算利用复制原理所建组合中借款的数额为多少?正确答案: 借款数额=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+持有期无风险利率)=(24×0.61-0)/(1+2%)=14.35(元)解析: 暂无解析 -
第13题:
假设该公司的股票现在市价为45元。有1股以该股票为标的资产的看涨期权,执行价格为48元,到期时间是6个月。6个月以后股价有两种可能:上升33.33%,或者下降25%,年无风险报价利率为4%,则利用复制原理确定期权价格时,下列说法错误的有( )。A.股价上行时期权到期日价值12元
B.套期保值比率为0.8
C.购买股票支出20.57元
D.以无风险利率借入14元答案:B,D解析:上行股价Su=股票现价×上行乘数=45×(1+33.33%)=60(元)
下行股价Sd=股票现价×下行乘数=45×(1-25%)=33.75(元)
股价上行时期权到期日价值Cu=上行股价-执行价格=60-48=12(元)
股价下行时期权到期日价值Cd=0
套期保值比率H=期权价值变化/股价变化=(12-0)/(60-33.75)=0.4571
购买股票支出=套期保值比率×股票现价=0.4571×45=20.57(元)
借款=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r)=(33.75×0.4571-0)/(1+2%)=15.12(元)。 -
第14题:
假设某公司股票现行市价为55元。有1份以该股票为标的资产的看涨期权,执行价格为60元,到期时间是6个月。6个月以后股价有两种可能:上升42%,或者下降29%。无风险年利率为4%,则利用风险中性原理所确定的期权价值为( )元。A、7.75
B、5.93
C、6.26
D、4.37答案:A解析:上行股价=55×(1+42%)=78.1(元)
下行股价=55×(1-29%)=39.05(元)
股价上行时期权到期日价值Cu=上行股价-执行价格=78.1-60=18.1(元)
股价下行时期权到期日价值Cd=0
期望回报率=2%=上行概率×42%+下行概率×(-29%)
2%=上行概率×42%+(1-上行概率)×(-29%)
上行概率=0.4366
下行概率=1-0.4366=0.5634
期权6个月后的期望价值=0.4366×18.1+0.5634×0=7.90(元)
期权的现值=7.90/1.02=7.75(元)。@## -
第15题:
假设ABC 公司的股票现在的市价为60 元。有1 股以该股票为标的资产的看涨期权,执行价格为65 元,到期时间是6 个月。6 个月以后股价有两种可能:上升22.56%或者降低18.4%。无风险报酬率为每年4%,假设该股票不派发红利,则利用风险中性原理计算期权价值过程中涉及的下列数据,不正确的是( )。A.股价上行时期权到期日价值为8.536 元
B.期望报酬率为4%
C.下行概率为0.5020
D.期权的现值为4.1675 元答案:B解析:上行股价=60×1.2256=73.536(元)下行股价=60×(1-18.4%)=48.96(元)股价上行时期权到期日价值=上行股价-执行价格=73.536-65=8.536(元)股价下行时期权到期日价值=0期望报酬率=2%=上行概率×22.56%+下行概率×(-18.4%)2%=上行概率×22.56%+(1-上行概率)×(-18.4%)上行概率=0.4980下行概率=1-0.4980=0.5020期权6 月后的期望价值=0.4980×8.536+0.5020×0=4.2509期权的现值=4.2509/1.02=4.1675(元) -
第16题:
假设ABC公司的股票现在的市价为60元。6个月以后股价有两种可能:上升33.33%,或者降低25%。有1股以该股票为标的资产的看涨期权,在利用复制原理确定其价值时,如果已知股价下行时的到期日价值为0,套期保值比率为0.6,则该期权的执行价格为( )元。A.80
B.60
C.59
D.62答案:C解析:上行股价=股票现价×上行乘数=60×1.3333=80(元),下行股价=股票现价×下行乘数=60×0.75=45(元),设执行价格为X,则:套期保值比率=(80-X-0)/(80-45)=0.6,解之得:X=59(元)。 -
第17题:
假设C公司股票现在的每股市价为10元,有1股以该股票为标的资产的看涨期权,执行价格为6元,到期时间为6个月。6个月后股价有两种可能:上升25%或者降低20%,无风险利率为每年4%。现在打算购进适量的股票以及借入必要的款项建立一个投资组合,使得该组合6个月后的价值与购进该看涨期权相等。
要求:
(1)确定可能的到期日股票价格。
(2)根据执行价格计算确定期权到期日价值。
(3)计算套期保值比率。
(4)计算购进股票的数量和借款数额。
(5)根据上述结果计算期权价值。
(6)如果该看涨期权的现行价格为6.12元,请根据套利原理,构建一个投资组合进行套利,并计算获利金额。答案:解析:(1)上行股价=10×(1+25%)=12.5(元)
下行股价=10×(1-20%)=8(元)(1分)
(2)股价上行时期权到期日价值=12.5-6=6.5(元)
股价下行时期权到期日价值=8-6=2(元)(1分)
(3)套期保值比率=(6.5-2)/(12.5-8)=1(1分)
(4)购进股票的数量=套期保值比率=1(股)
借款本金=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+4%×6/12)=(8×1-2)/(1+2%)=5.88(元)(2分)
提示:在建立对冲组合时:
股价下行时期权到期日价值=股价下行时到期日股票出售收入-偿还的借款本利和=到期日下行股价×套期保值比率-借款本金×(1+r)
由此可知:
借款本金=(到期日下行股价×套期保值比率-股价下行时期权到期日价值)/(1+r)
(5)期权价值=购买股票支出-借款=1×10-5.88=4.12(元)(1分)
(6)由于期权价格高于期权价值,因此,套利投资组合如下:买入1股股票,借入5.88元,同时卖出1股看涨期权。(1分)
获利=6.12+5.88-1×10=2(元)(1分) -
第18题:
某股票现在的市价为10元,有1股以该股票为标的资产的看涨期权,执行价格为10.7元,到期时间是6个月。6个月以后股价有两种可能:上升25%,或者下降20%。无风险报酬率为6%,则根据复制组合原理,该期权价值是()元。
- A、3.2
- B、0
- C、1.8
- D、0.89
正确答案:D -
第19题:
单选题假设ABC公司的股票现在的市价为60元。6个月以后股价有两种可能:上升33.33%,或者降低25%。有1股以该股票为标的资产的看涨期权,在利用复制原理确定其价值时,如果已知股价下行时的到期日价值为0,套期保值比率为0.6,则该期权的执行价格为()元。A59
B60
C62
D65
正确答案: A解析: 上行股价=股票现价×上行乘数=60×1.3333=80(元)下行股价=股票现价×下行乘数=60×0.75=45(元)设执行价格为r元,则:套期保值比率=(80-x-0)/(80-45)=0.6解之得:x=59(元) -
第20题:
问答题假设ABC公司的股票现在的市价为30元。有1份以该股票为标的资产的看涨期权,执行价格为30.5元,到期时间是6个月。6个月以后股价有两种可能:上升35%,或者下降20%。无风险利率为每年4%。拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合6个月后的价值与购进该看涨期权相等。如果该看涨期权的现行价格为4元,请根据套利原理,构建一个投资组合进行套利。正确答案: 由于目前看涨期权价格为4元,高于3.95元,所以存在套利空间。套利组合应为:按4元出售1份看涨期权,卖空14.35元的无风险证券,买入0.61股股票,进行套利,可套利0.05元。解析: 暂无解析 -
第21题:
单选题假设ABC公司的股票现在的市价为40元。有1股以该股票为标的资产的看涨期权,执行价格为45元,到期时间6个月。6个月以后股价有两种可能:上升20%,或者降低16.67%。无风险利率为每年8%,则上行概率为( )。A67.27%
B56.37%
C92.13%
D73.54%
正确答案: C解析:
股票上行乘数u=1+20%=1.2,股票下行乘数d=1-16.67%=0.8333;无风险利率为每年8%,到期时间为6个月,所以r=4%;上行概率=(1+r+d)/(u-d)=(1+4%-0.8333)/(1.2-0.8333)=56.37%,或者:上行概率=(r+下降百分比)/(上升百分比+下降百分比)=(4%+16.67%)/(20%+16.67%)=56.37%。 -
第22题:
问答题假设ABC公司的股票现在的市价为30元。有1份以该股票为标的资产的看涨期权,执行价格为30.5元,到期时间是6个月。6个月以后股价有两种可能:上升35%,或者下降20%。无风险利率为每年4%。拟利用复制原理,建立一个投资组合,包括购进适量的股票以及借入必要的款项,使得该组合6个月后的价值与购进该看涨期权相等。期权的价值为多少?正确答案: 期权价值=投资组合成本=购买股票支出-借款=0.61×30-14.35=3.95(元)解析: 暂无解析 -
第23题:
问答题假设甲公司的股票现在的市价为20元。有1份以该股票为标的资产的看涨期权,执行价格为21元,到期时间是1年。1年以后股价有两种可能:上升40%,或者下降30%。无风险利率为每年4%。要求:利用风险中性原理确定期权的价值。正确答案: 期望报酬率=4%=上行概率×40%+(1-上行概率)×(-30%)上行概率=0.4857,
下行概率=1-0.4857=0.5143,
股价上行时期权到期日价值Cd=20×(1+40%)-21=7(元),
股价下行时期权到期日价值Cd=0
期权现值=(上行概率×股价上行时期权到期日价值+下行概率×股价下行时期权到期日价值)÷(1+持有期无风险利率)
=(7×0.4857+0×0.5143)÷(1+4%)
=3.3999/1.04=3.27(元)解析: 暂无解析
