甲公司打算购买A公司刚发行的5年期公司债券，每张面值为1000元，票面利率为8%。假定该债券每年付息一次，到期按面值偿还，投资者要求的必要报酬率为10%。根据上述资料计算当每张债券价格最高为（ ）元时，甲公司才可以考虑购买。 A、1200 B、924.16 C、856.32 D、1080.69
题目
甲公司打算购买A公司刚发行的5年期公司债券，每张面值为1000元，票面利率为8%。假定该债券每年付息一次，到期按面值偿还，投资者要求的必要报酬率为10%。根据上述资料计算当每张债券价格最高为（ ）元时，甲公司才可以考虑购买。
A、1200
B、924.16
C、856.32
D、1080.69
B、924.16
C、856.32
D、1080.69
相似考题
更多“甲公司打算购买A公司刚发行的5年期公司债券，每张面值为1000元，票面利率为8%。假定该债券每年付息一次，到期按面值偿还，投资者要求的必要报酬率为10%。根据上述资料计算当每张债券价格最高为（ ）元时，甲公司才可以考虑购买。 ”相关问题
-
第1题：
A公司拟于2007年年初购买某公司债券作为长期投资(打算持有至到期日)，要求的必要收益率为6%。现有两家公司计划于2007年年初发行5年期，面值均为1000元的债券。其中：甲公司债券的票面利率为8%，单利计息，到期一次还本付息，债券发行价格为1050元；乙公司债券的票面利率为0，债券发行价格为750元，到期按面值还本。
要求：
(1)计算甲债券的价值和持有期年均收益率；
(2)计算乙债券的价值；
(3)根据上述计算结果，评价甲、乙债券是否具有投资价值。
正确答案：
(1)甲公司债券的价值=1000×(1+5×8％)×(P／F，6％，5) =1400×0.7473=1046.22(元)
令甲公司债券的持有期年均收益率为i，则：
(2)乙公司债券的价值=1000×(P／F，6％，5)=1000×0.7473=747.3(元)
(3)甲公司债券的价值1046.22元<目前的市价1050元(或甲债券的投资收益率5.92％小于必要收益率6％)，因此不具有投资价值。乙公司债券的价值747.3元<目前的市价750元，也不具有投资价值。 -
第2题：
甲欲投资购买债券，要求的最低报酬率为10%，有两家公司债券可供选择：
(1)A公司债券期限为5年，属于可转换债券，转换比率为40，转换期为5年，每张债券面值为1000元，票面利率为5%，到期一次还本付息。已经发行2年，目前价格为1050元。甲打算购入两年后转换为普通股，预计每股市价为30元，转股之后可以立即出售。甲投资者计划购买100张该债券。
(2)B公司债券期限为4年，每年付息一次，每次付息60元，到期还本1000元。已发行2.5年。
要求：
(1)计算该债券的转换价格，甲投资者可以转换的普通股数，目前每张该债券的价值，并判断是否值得购买；
(2)计算该债券的价格为多少时甲才会购买。已知：(P/F，10%，1)=0.9091，(P/F，10%，2)=0.8264
正确答案：
(1)转换价格=1000/40=25(元/股)
甲投资者可以转换的普通股数=100×40=4000(股)
甲在转换之前无法收到利息，持有期间的收入只有股票出售收入。
每张债券转换成股票出售的收入是：40 × 30=1200(元)
债券价值=1200×(P/F，10%，2)=991.68(元)
由于A公司债券价格1050元高于债券价值991.68元，所以，A公司债券不值得购买。
(2)B公司债券1.5年后到期，投资该债券0.5年、1.5年后分别可以收到60元利息，1.5年后还可以收到1000元返回的本金。
债券在0.5年后的价值=60+60×(P/F，10%，1)+1000×(P/F，10%，1)=1023.65(元)
债券目前的价值=1023.65×(P/F，10%，1/2)=1023.65÷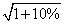
=976.01(元)
所以，只有当债券的价格低于976.01元时，甲才会购买。
-
第3题：
甲公司欲投资购买债券，打算持有至到期日，要求的必要收益率为6%（复利、按年计息），目前有三种债券可供挑选：
＜1>、A债券面值为1000元，5年期，票面利率为8%，每年付息一次，到期还本，A债券是半年前发行的，现在的市场价格为1050元，计算A公司债券目前的价值为多少？是否值得购买？
＜2>、B债券面值为1000元，5年期，票面利率为8%，单利计息，利随本清，目前的市场价格为1050元，已经发行两年，计算B公司债券目前的价值为多少？是否值得购买？
＜3>、C债券面值为1000元，5年期，四年后到期，目前市价为600元，期内不付息，到期还本， 计算C债券的到期收益率为多少？是否值得购买？
＜4>、若甲公司持有B公司债券2年后，将其以1200元的价格出售，则投资报酬率为多少？答案：解析：A债券半年后的价值
＝80＋80×（P/A，6%，4）＋1000×（P/F，6%，4）
＝80＋80×3.4651＋1000×0.7921
＝1149.31（元）（1分）
A债券目前的价值
＝1149.31×（P/F，6%，1/2）
＝1149.31×0.9713
＝1116.32（元）（0.5分）
由于A债券目前的价值高于其价格1050元，所以应该购买。（0.5分）
【考点“债券的到期收益率”】
B债券的价值＝1000×（1＋8%×5）×（P/F，6%，3）＝1400×0.8396＝1175.44（元）（1分）
由于B债券目前的价值高于其价格1050元，所以值得购买。（1分）
【考点“债券的到期收益率”】
设C债券的到期收益率为r，则：
600＝1000×（P/F，r，4）（0.5分）
（P/F，r，4）＝0.6
（F/P，r，4）＝1.667
（1+r）4＝1.667
则：r＝1.667 1/4－1＝13.63%（1分）
由于C债券的到期收益率（13.63%）高于投资人要求的必要收益率（6%），所以值得购买。（0.5分）
【考点“债券的到期收益率”】
设投资报酬率为r，则：
1200×（P/F，r，2）＝1050（1分）
即：1050×（1+r）2=1200
（1分）
【考点“债券的到期收益率”】 -
第4题：
A公司2016年6月5日发行公司债券，每张面值1000元，票面年利率10%，4年期。
要求：
（1）假定每年6月4日付息一次，到期按面值偿还。B公司2018年6月5日按每张1000元的价格购入该债券并持有到期，计算该债券的内部收益率。
（2）假定每年6月4日付息一次，到期按面值偿还。B公司2018年6月5日按每张1020元的价格购入该债券并持有到期，计算该债券的内部收益率。
（3）假定每年6月4日付息一次，到期按面值偿还。B公司2017年6月5日购入该债券并持有到期，市场利率为12%，计算该债券的价格低于多少时可以购入。答案：解析：（1）由于该债券属于分期付息、到期还本的平价债券，所以，内部收益率=票面利率=10%。
（2）NPV=1000×10%×（P/A，i，2）+1000×（P/F，i，2）-1020
当i=10%，NPV=1000×10%×（P/A，10%，2）+1000×（P/F，10%，2）-1020=-20（元）
当i=8%，NPV=1000×10%×（P/A，8%，2）+1000×（P/F，8%，2）-1020=15.63（元）
i=8%+（0?15.63）/（?20?15.63）×（10%-8%）=8.88%。
【彩蛋】压卷，瑞牛题库软件考前更新，下载链接 www.niutk.com
（3）债券的价值=1000×10%×（P/A，12%，3）+1000×（P/F，12%，3）=100×2.4018+1000×0.7118=951.98（元），当债券的价格低于951.98元时可以购入。 -
第5题：
甲公司2019年4月8日发行公司债券，每张面值1000元，票面年利率6％，5年期。
要求：
(1)假定每年4月7日付息一次，到期按面值偿还。如果乙公司可以在2021年4月8日按每张1000元的价格购入该债券并持有至到期，计算该债券的内部收益率。
(2)假定每年4月7日付息一次，到期按面值偿还。如果丙公司可以在2021年4月8日按每张1009元的价格购入该债券并持有至到期，计算该债券的内部收益率。
(3)假定每年4月7日付息一次，到期按面值偿还。丁公司计划在2020年4月8日购入该债券并持有至到期，要求的最低投资报酬率为8％，计算该债券的价格低于多少时可以购入。答案：解析：(1)由于该债券属于分期付息、到期还本的平价债券，所以，内部收益率=票面利率=6％。
(2)NPV=1000×6％×(P／A，i，3)+1000×(P／F，i，3)-1009
当i=6％，NPV=1000×6％×(P／A，6％，3)+1000×(P／F，6％，3)-1009=-9(元)
当i=5％，NPV=1000×6％×(P／A，5％，3)+1000×(P／F，5％，3)-1009=18．19(元)
i=5％+(0-18．19)／(-9-18．19)×(6％-5％)=5．67％
(3)债券的价值=1000×6％×(P／A，8％，4)+1000×(P／F，8％，4)
=60×3．3121+1000×0．735
=933．73(元)
因此当债券的价格低于933．73元时可以购入。 -
第6题：
已知：甲公司股票必要报酬率为12％。乙公司2007年1月1日发行公司债券，每张面值1000元，票面利率8％，5年期。 要求回答下列互不相关的问题：假定乙公司的债券是每年12月31日付息一次，到期按面值偿还，必要报酬率为10％。B公司2010年1月1日打算购入该债券并持有到期，计算确定当债券价格为多少时，B公司才可以考虑购买。已知：（P／F，12％，3）=0．7118，（P／A，12％，3）=2．4018，（P／F，10％，1）=0．9091（P／F，10％，2）=0．8264，（P／F，12％，1）=0．8929，（P／F，12％，2）=0．7972，（P／A，10％，2）=1．7355
正确答案:债券价值=1000×8％×(P／A，10％，2)+1000×(P／F，10％，2)=80×1．7355+1000×0．8264=965．24(元)，所以，当债券价格低于965．24元时，B公司才可以考虑购买。 -
第7题：
问答题计算分析题：已知：甲公司股票必要报酬率为12%。乙公司2007年1月1日发行公司债券，每张面值1000元，票面利率8%，5年期。要求：回答下列互不相关的问题：（1）若甲公司的股票未来三年股利为零增长，每年股利为1元／股，预计从第4年起转为正常增长，增长率为5%，则该股票的价值为多少？（2）若甲公司股票目前的股价为20元，预计未来两年股利每年增长10%，预计第1年股利为1元／股，从第3年起转为稳定增长，增长率为5%，则该股票的投资收益率为多少？（提示：介于10%和12%之间）（3）假定乙公司的债券是到期一次还本付息，单利计息。B公司2011年1月1日按每张1200元的价格购入该债券并持有至到期，计算该债券的到期收益率。（4）假定乙公司的债券是每年12月31日付息一次，到期按面值偿还，必要报酬率为10%。B公司2010年1月1日打算购入该债券并持有至到期，计算确定当债券价格为多少时，B公司才可以考虑购买。正确答案： （1）股票价值=1×（P/A，12%，3）+1×（1+5%）／12%-5%）×（P／F，12%，3）=1×2.4018+15×0.7118=13.08（元）（2）设投资收益率为r，则20=1×（P/F，r，1）+1×（1+10%）×（P/F，r，2）+1×（1+10%）×（1+5%）／（r-5%）×（P／F，r，2）即：20=1×（P/F，r，1）+1.1×（P/F，r，2）+1.155/（r-5%）×（P/F，r，2）20=1×（P/F，r，1）+［1.1+1.155/（r-5%）］×（P／F，r，2）当r=10%时，1×（P／F，10%，1）+［1.1+1.155/（10%-5%）］×（P／F，10%，2）=20.908（元）当r=12%时，1×（P/F，12%，1）+［1.1+1.155/（12%-5%）］×（P／F，12%，2）=14.924（元）利用内插法可知：（20.908-20）/（20.908-14.924）=（10%-r）/（10%-12%）解得：r=10.30%（3）1000×（1+5×8%）／（1+i）=1200，求得i=16.67%（4）债券价值=1000×8%×（P／A，10%，2）+1000×（P/F，10%，2）=80×1.7355+1000×0.8264=965.24（元）所以，当债券价格低于965.24元时，B公司才可以考虑购买。解析： 暂无解析 -
第8题：
问答题甲公司2002年4月8日发行公司债券，债券面值1000元，票面利率10%，5年期。假定该债券每年4月8日付息一次，到期按面值偿还。乙公司2004年4月8日计划购入该债券并持有到期，要求的必要报酬率为12%（可视为市场利率），则该债券的价格为多少时乙公司可以购入？正确答案： V＝1000×10%×2.402＋1000×0.712＝952.2解析： 暂无解析 -
第9题：
问答题甲公司2002年4月8日发行公司债券，债券面值1000元，票面利率10%，5年期。假定该债券到期一次还本付息，单利计息。乙公司2004年4月8日计划购入该债券并持有到期，要求的必要报酬率为12%，则该债券的价格为多少时乙公司可以购入？正确答案： V＝1000×（1＋10%×5）/（1+12%）＝1339.29解析： 暂无解析 -
第10题：
问答题已知：A公司拟购买某公司债券作为长期投资（打算持有至到期日），要求的必要收益率为6％。现有三家公司同时发行5年期，面值均为1000元的债券，其中：甲公司债券的票面利率为8％，每年付息一次，到期还本，债券发行价格为1041元；乙公司债券的票面利率为8％，单利计息，到期一次还本付息，按复利折现，债券发行价格为1050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。部分货币时间价值系数如下。根据上述计算结果，评价甲、乙、丙三种公司债券是否具有投资价值，并为A公司作出购买何种债券的决策。正确答案： 由于甲公司债券的价值高于其买价，甲公司债券具有投资价值；而乙公司和丙公司债券的价值均低于其买价，不具有投资价值。A公司应购买甲公司债券。解析： 暂无解析 -
第11题：
问答题已知：A公司拟购买某公司债券作为长期投资（打算持有至到期日），要求的必要收益率为6％。现有三家公司同时发行5年期，面值均为1000元的债券，其中：甲公司债券的票面利率为8％，每年付息一次，到期还本，债券发行价格为1041元；乙公司债券的票面利率为8％，单利计息，到期一次还本付息，按复利折现，债券发行价格为1050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。部分货币时间价值系数如下。计算A公司购入丙公司债券的价值。正确答案： 丙公司债券的价值=1000×(P／F，6％，5)=1000×0．7473=747．3(元)解析： 暂无解析 -
第12题：
问答题ABC公司欲投资购买债券，目前有四家公司正在发行债券： （1）A公司债券，债券面值为1000元，5年期，票面利率为8%，每年付息一次，到期还本，债券的发行价格为1105元，若等风险的必要报酬率为6%，则A公司债券的价值与到期收益率为多少？应否购买？ （2）B公司债券，债券面值为1000元，5年期，票面利率为8%，单利计息，到期一次还本付息，债券的发行价格为1105元，若投资人要求的必要报酬率为6%（复利，按年计息），则B公司债券的价值与到期收益率（复利，按年计息）为多少？应否购买？ （3）C公司债券属于纯贴现债券，债券面值为1000元，5年期，发行价格为600元，期内不付息，到期还本，若等风险的必要报酬率为6%，则C公司债券的价值与到期收益率为多少？应否购买？ （4）D公司债券，债券面值为1000元，5年期，票面利率为8%，每半年付息一次，到期还本，债券的发行价格为1085.31元，若年折现率为6.09%，则D公司债券的价值与到期收益率为多少？应否购买？正确答案：
(1)A债券的价值=1000×8%×(P/A,6%,5)+1000×(P/F,6%,5)=80×4.2124+1000×0.7473=1084.29(元);设i=5%,1000×8%×(P/A,5%,5)+1000×(P/F,5%,5)=80×4.3295+1000×0.7835=1129.86(元);插值法:债券到期收益率i=5%+(1129.86-1105)/(1129.86-1084.29)×(6%-5%)=5.55%。
由于债券价值1084.29<债券发行价格1105,所以不应购买。
(2)因为该债券单利计息且到期一次还本付息,所以:B债券的价值=1000×(1+5×8%)×(P/F,6%,5)=1400×0.7473=1046.22(元);
再求债券的到期收益率,可通过等式1105=1000×(1+5×8%)×(P/F,i,5),
解得(P/F,i,5)=1105/1400=0.7893;插值法:i=5%,(P/F,5%,5)=0.7835,i=4%,(P/F,4%,5)=0.8219;
所以,债券到期收益率=4%+(5%-4%)×(0.8219-0.7893)/(0.8219-0.7835)=4.85%。由于债券价值1046.22<债券发行价格1105,所以不应购买。
(3)因为C公司债券属于纯贴现债券,故C债券的价值=1000×(P/F,6%,5)=747.3(元);
再求债券的到期收益率:600=1000×(P/F,i,5),则(P/F,i,5)=0.6;插值法:i=10%,(P/F,i,5)=0.6209,i=12%,(P/F,i,5)=0.5674;
所以,债券到期收益率=10%+(0.6209-0.6)/(0.6209-0.5674)×(12%-10%)=10.78%。由于债券价值747.3>债券发行价格600,所以应购买。
(4)因为债券每半年付息一次,每半年期的折现率为(1+6.09%)1/2-1=3%,所以D债券的价值=1000×4%×(P/A,3%,10)+1000×(P/F,3%,10)=1085.31(元);由于价值等于发行价格,所以可以购买。有效年到期收益率=年折现率=6.09%。解析： 暂无解析 -
第13题：
甲公司2003年1月1日发行新债券，每张面值1 000元，票面利率10%，5年期，每年12月1日付息一次，到期按面值偿还。
要求：
(1)假定2003年1月1日的市场利率为l2%，债券发行价格低于多少时公司将可能取消发行计划?
(2)若乙公司按面值购买该债券，计算该债券的票面收益率。
(3)假定2005年1月1日的市价为940元，此时乙公司购买该债券的本期收益率是多少?
若乙公司持有该债券到2007年1月1日卖出，每张售价990元，计算该债券的持有期收益率。
(4)假定2006年1月1日乙公司以每张970元的价格购买该债券，计算该债券的到期收益率。
正确答案：
(1)债券发行价格的下限应是按l2%计算的债券价值。
债券价值=1 000×10%×(P/A，12%，5)+1 000×(P/S，12%，5)
=100×3.6048+1 000×0.5674
=927.88(元)。
即发行价格低于927.88元时，公司将可能取消发行计划。
(2)该债券的票面收益率=1 000×10%÷1 000=10%。
(3)乙公司购买该债券的本期收益率=1 000×10%÷940=10.64%；
持有期收益率=[1 000×10%+(990-940)÷2]÷940=13.30%。
(4)根据970=1 000×10%(P/A，1，2)+1 000×(P/F，1，2)
970=100×(P/A，1，2)+1 000×(P／F，1，2)
1=10%，NPV=1 000-970=30；
1=12%，NPV=966.21-970=-3.79；
采用插值法，得到本期收益率=11.78%。 -
第14题：
已知：A公司拟购买某公司债券作为长期投资(打算持有至到期日)，要求的必要收益率为6%。
现有三家公司同时发行5年期，面值均为1 000元的债券。其中：甲公司债券的票面利率为8%，每年付息一次，到期还本，债券发行价格为1 041元；乙公司债券的票面利率为8%，单利计息，到期一次还本付息，债券发行价格为1 050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。
要求：
(1)计算A公司购入甲公司债券的价值和收益率。
(2)计算A公司购入乙公司债券的价值和收益率。
(3)计算A公司购入丙公司债券的价值。
(4)根据上述计算结果，评价甲、乙、丙三种公司债券是否具有投资价值，并为A公司做出购买何种债券的决策。
(5)若A公司购买并持有甲公司债券，1年后将其以1 050元的价格出售，计算该项投资收益率。
正确答案：(1)甲债券的价值=1 000×8%×(P/A，6%，5)+1 000(P/F，6%，5)=1 084.29(元)
测试7%
1 000×8%×(P/A，7%，5)+1 000×(P/F,7%，5)=1 041(元)
∴ 收益率为7%。
(2)乙债券的价值
=1 000×(1+5×8%)×(P/F，6%，5)=1 046.22(元)
测试5%
1 000×(1+5×8%)×(P/F，5%，5)=1 096.9(元)
收益率=5%+(1096.9-1050)/(1096.9-1046.22)×(6%-5%)=5.93%
(3)丙债券的价值=1 000×(P/F，6%，5)=747.3(元)
(4)甲公司的债券具有投资价值。
(5)K=1050-1041+1000×8%=8.55% -
第15题：
B 公司 2010 年 1 月 1 日发行公司债券，每张面值 1000 元，票面利率 8%，5 年期。B 公司适用的所得税税率为 25%。
通过计算回答下列互不相关的几个问题：'
1） 假定每年1 月1 日付息一次，到期按面值偿还。发行价格为1030 元／张，发行费用为8 元／张，计算该债券的税后资本成本。
2） 假定每年付息两次，每间隔6 个月付息一次，到期按面值偿还。C 公司2013 年1月1 日按每张1020 元的价格购入该债券并持有到期，计算该债券的有效年到期收益率。
3） 假定每年付息两次，每间隔6 个月付息一次，到期按面值偿还。折现率为10%，甲公司2012 年1 月1 日打算购入该债券并持有到期，计算确定当债券价格低于什么水平时，甲公司才可以考虑购买。答案：解析：1）假设债券的税前资本成本为i，则有：
1000×8%×（P／A，i，5）＋1000×（P／F，i，5）＝（1030－8）（1 分）
当i＝8%时，1000×8%×（P／A，8%，5）＋1000×（P／F，8%，5）＝1000.02
当i＝7%时，1000×8%×（P／A，7%，5）＋1000×（P／F，7%，5）＝1041.02
运用内插法，列式为（i－7%）／（8%－7%）＝（1022－1041.02）／（1000.02－1041.02）
解得i＝7.46%（1 分）
债券的税后资本成本＝7.46%×（1－25%）＝5.60%（1 分）
2）设半年到期收益率为i，则有：
1000×4%×（P／A，i，4）＋1000×（P／F，i，4）＝1020（1 分）
当i＝4%时，1000×4%×（P／A，4%，4）＋1000×（P／F，4%，4）＝1000
当i＝3%时，1000×4%×（P／A，3%，4）＋1000×（P／F，3%，4）＝1037.18
运用内插法，列式为（i－3%）／（4%－3%）＝（1020－1037.18）／（1000－1037.18）
解得i＝3.46%（1 分）
债券的有效年到期收益率＝（1＋3.46%）2－1＝7.04%（1 分）
3）】债券价值＝1000×4%×（P／A，5%，6）＋1000×（P／F，5%，6）
＝40×5.0757＋1000×0.7462
＝949.23（元）（1 分）
所以，当债券价格低于949.23 元时，甲公司才可以考虑购买 -
第16题：
甲公司2020年4月8日发行公司债券，每张面值1000元，票面年利率6%，5年期。
要求：
（1）假定每年4月7日付息一次，到期按面值偿还。如果乙公司可以在2022年4月8日按每张1000元的价格购入该债券并持有至到期，计算该债券的内部收益率。
（2）假定每年4月7日付息一次，到期按面值偿还。如果丙公司可以在2022年4月8日按每张1009元的价格购入该债券并持有至到期，计算该债券的内部收益率。
（3）假定每年4月7日付息一次，到期按面值偿还。丁公司计划在2021年4月8日购入该债券并持有至到期，要求的最低投资收益率为8%，计算该债券的价格低于多少时可以购入。答案：解析：（1）由于该债券属于分期付息、到期还本的平价债券，所以，内部收益率=票面利率=6%。
（2）NPV=1000×6%×（P/A，i，3）+1000×（P/F，i，3）-1009
当i=6%，NPV=1000×6%×（P/A，6%，3）+1000×（P/F，6%，3）-1009=-9（元）
当i=5%，NPV=1000×6%×（P/A，5%，3）+1000×（P/F，5%，3）-1009=18.19（元）
i=5%+（0-18.19）/（-9-18.19）×（6%-5%）=5.67%
（3）债券的价值=1000×6%×（P/A，8%，4）+1000×（P/F，8%，4）=60×3.3121+1000×0.735=933.73（元）
因此当债券的价格低于933.73元时可以购入。 -
第17题：
甲公司2002年4月8日发行公司债券，债券面值1000元，票面利率10%，5年期。假定每年4月8日付息一次，到期按面值偿还。乙公司于2006年4月8日按每张1020元的价格购入该债券，并持有到期。求债券的到期收益率为多少？
正确答案: 到期收益率＝[1000×（1+10%）-1020]/1020＝7.84% -
第18题：
问答题甲公司2002年4月8日发行公司债券，债券面值1000元，票面利率10%，5年期。假定每年4月8日付息一次，到期按面值偿还。乙公司于2006年4月8日按每张1020元的价格购入该债券，并持有到期。求债券的到期收益率为多少？正确答案： 到期收益率＝[1000×（1+10%）-1020]/1020＝7.84%解析： 暂无解析 -
第19题：
问答题已知：A公司拟购买某公司债券作为长期投资（打算持有至到期日），要求的必要收益率为6％。现有三家公司同时发行5年期，面值均为1000元的债券，其中：甲公司债券的票面利率为8％，每年付息一次，到期还本，债券发行价格为1041元；乙公司债券的票面利率为8％，单利计息，到期一次还本付息，按复利折现，债券发行价格为1050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。部分货币时间价值系数如下。计算A公司购入乙公司债券的价值和内部收益率。正确答案： 乙公司债券的价值=（1000×8％×5+1000）×（P／F，6％，5）=1400×0.7473=1046.22（元）设内部收益率为i：（1000×8％×5+1000）×（P／F，i，5）=1050当利率为5％：（1000×8％×5+1000）×（P／F，5％，5）=1400×0.7835=1096.9（元）所以乙公司债券的内部收益率为5.93％。解析： 暂无解析 -
第20题：
问答题甲公司2002年4月8日发行公司债券，债券面值1000元，票面利率10%，5年期。假定该债券到期一次还本付息，单利计息。乙公司于2006年4月8日按每张1380元的价格购入该债券并持有到期。则债券的到期收益率为多少？正确答案： 到期收益率＝[1000×（1+10%×5）-1380]/1380＝8.70%解析： 暂无解析 -
第21题：
问答题已知：A公司拟购买某公司债券作为长期投资（打算持有至到期日），要求的必要收益率为6％。现有三家公司同时发行5年期，面值均为1000元的债券，其中：甲公司债券的票面利率为8％，每年付息一次，到期还本，债券发行价格为1041元；乙公司债券的票面利率为8％，单利计息，到期一次还本付息，按复利折现，债券发行价格为1050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。部分货币时间价值系数如下。若A公司购买并持有甲公司债券，2年后将其以1050元的价格出售，利用简便算法计算该项投资收益率。正确答案：解析： 暂无解析 -
第22题：
问答题已知：A公司拟购买某公司债券作为长期投资（打算持有至到期日），要求的必要收益率为6％。现有三家公司同时发行5年期，面值均为1000元的债券，其中：甲公司债券的票面利率为8％，每年付息一次，到期还本，债券发行价格为1041元；乙公司债券的票面利率为8％，单利计息，到期一次还本付息，按复利折现，债券发行价格为1050元；丙公司债券的票面利率为零，债券发行价格为750元，到期按面值还本。部分货币时间价值系数如下。计算A公司购入甲公司债券的价值和内部收益率。正确答案： 甲公司债券的价值=1000×8％×（P／A，6％，5）+1000×（P／F，6％，5）=80×4.2124+1000×0.7473=1084.29（元）设内部收益率为i：1000×8％×（P／A，i，5）+1000×（P／F，i，5）=1041当利率为7％：1000×8％×（P／A，7％，5）+1000×（P／F，7％，5）=1041（元）所以甲公司债券的内部收益率=7％解析： 暂无解析 -
第23题：
问答题A公司2017年6月5日发行公司债券，每张面值1000元，票面利率10%，4年期。要求：(1)假定每年6月4日付息一次，到期按面值偿还。B公司2019年6月5日按每张1000元的价格购人该债券并持有至到期，计算该债券的持有至到期收益率。(2)假定每年6月4日付息一次，到期按面值偿还。B公司2019年6月5日按每张1020元的价格购人该债券并持有至到期，计算该债券的持有至到期收益率。(3)假定每年6月4日付息一次，到期按面值偿还。B公司2018年6月5日购入该债券并持有至到期，要求的必要报酬率为12%,计算该债券的价格低于多少时可以购入。(4)假定到期一次还本付息，单利计息。B公司2018年6月5日购入该债券并持有至到期，要求的必要报酬率为12%，计算该债券的价格低于多少时可以购人。（按复利折现）正确答案：解析：