函数曲线y＝1n(1＋x2)的凹区间是（）A.(－1，1) B.(－∞，－1) C.(1，＋∞) D.(－∞，＋∞)

题目
函数曲线y＝1n(1＋x2)的凹区间是（）

A.(－1，1)
B.(－∞，－1)
C.(1，＋∞)
D.(－∞，＋∞)
相似考题

1.曲线y=e^x－e^－x的凹区间是()A、(-∞,0)B、(0,+∞)C、(-∞,1)D、(-∞,+∞)

2.已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．（I）求a，b；（II）求f（x）的单调区间，并说明它在各区间的单调性．

3.在(－1,1)区间上满足罗定理条件的函数是()A、y=xB、y=1/xC、y=x²D、y=/x/

4.(本题满分8分)求函数y＝x3-3x2-1的单调区间、极值及其曲线的凹凸区间和拐点。

更多“函数曲线y＝1n(1＋x2)的凹区间是（）”相关问题

  • 第1题：

    函数y=ex-1的反函数是(65)。

    A．y=1nx+1

    B．y=ln(x+1)

    C．y=1nx-1

    D．y=1n(x-1)


    正确答案：B
    解析：

  • 第2题：

    设曲线y=ln(1+x2)，M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1=0，则点M的坐标是( )。

    A.(-2，ln5)
    B.(-1，ln2)
    C.(1，ln2)
    D.(2，ln5)

    答案：C
    解析：
    在D选项中，利用函数在一点的导数的几何意义及平行的已知条件确定点的坐标

  • 第3题：

    确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点．


    答案：
    解析：

  • 第4题：

    函数y=ln(1+x2)的驻点为x=______．


    答案：
    解析：
    填0．

  • 第5题：

    求y=f(x)=2x3-3x2-12x+14的极值点和极值，以及函数曲线的凸凹性区间和拐点.


    答案：
    解析：
    y'=6x2-6x-12，y''=12x-6，令y'=0得驻点x1=-1,x2=2，当x2=2时，y''=18>0．所以f(z)在x=2处取极小值-6．当x1=-1时，y''<0．所以f(x)在x=-1处取极大值21．

  • 第6题：

    函数y=xlnx的单调增加区间是______．


    答案：
    解析：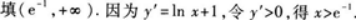

  • 第7题：

    微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：

    A.1+x2=Cy
    B. (1+x2)(3+2y)=C
    C.(3+2y)2=1/(1+x2)
    D. (1+x2)2(3+2y)=C

    答案：B
    解析：
    提示 判断方程的类型为可分离变量方程，将方程分离变量得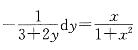dx，两边积分计算。

  • 第8题：

    求函数y=x-lnx的单调区间，并求该曲线在点(1，1)处的切线l的方程．


    答案：
    解析：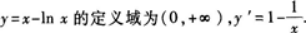


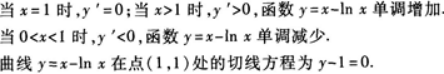
    【评析】求函数f(x)的单调区间，应先判定函数的定义域．求出函数的驻点，即y′=0的点；求出y的不可导的点，再找出y′>0时x的取值范围，这个范围可能是一个区间，也可能为几个区间．

  • 第9题：

    曲线y=x3（x-4）既单增又向上凹的区间为（）

    • A、（-∞，0）
    • B、（0，+∞）
    • C、（2，+∞）
    • D、（3，+∞）

    正确答案:D

  • 第10题：

    单选题
    设随机变量X的概率密度函数f（x）＝1/[π（1＋x2）]，则Y＝3X的概率密度函数为（　　）。
    A

    1/[π（1＋y2）]

    B

    3/[π（9＋y2）]

    C

    9/[π（9＋y2）]

    D

    27/[π（9＋y2）]


    正确答案： D
    解析：
    由y＝3x得x＝y/3，故fY（y）＝{1/π[1＋（y/3）2]}·（1/3）＝3/[π（9＋y2）]。

  • 第11题：

    单选题
    曲线y=2x+（8/x）在区间（0，2）内是（）。
    A

    单调增加、凸的

    B

    单调减少、凸的

    C

    单调增加、凹的

    D

    单调减少、凹的


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    曲线y=x3（x-4）既单增又向上凹的区间为：（）
    A

    （-∞，0）

    B

    （0，+∞）

    C

    （2，+∞）

    D

    （3，+∞）


    正确答案： D
    解析： 暂无解析

  • 第13题：

    曲线Y=x3（x-4）既单增又向上凹的区间为：

    A.（-∞，0）
    B.（0，+∞）
    C.（2，+∞）
    D.（3，+∞）

    答案：D
    解析：
    提示：经计算，函数的单增区间为（3，+∞），凹区间为（-∞，0 ），（2，+∞），故符合条件的区间为（3，+∞）。

  • 第14题：

    微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：
    A.1+x2=Cy B. (1+x2)(3+2y)=C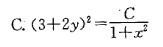
    D. (1+x2)2(3+2y)=C


    答案：B
    解析：
    提示:判断方程的类型为可分离变量方程，将方程分离变量得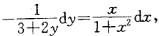两边
    积分计算。

  • 第15题：

    如果在区间(a，b)内，函数f(x)满足f′(x)>0，f′′(x)<0，则函数在此区间是()

    A.单调递增且曲线为凹的
    B.单调递减且曲线为凸的
    C.单调递增且曲线为凸的
    D.单调递减且曲线为凹的

    答案：C
    解析：
    【考情点拨】本题考查了函数的单调性和凹凸性的知识点．【应试指导】因f'(x)>0，故函数单调递增，又f''(x)<0．所以函数曲线为凸的．

  • 第16题：

    如果在区间(a，b)内，函数，(z)满足f’(x)>0，f"(x)<0，则函数在此区间是()

    A.单调递增且曲线为凹的
    B.单调递减且曲线为凸的
    C.单调递增且曲线为凸的
    D.单调递减且曲线为凹的

    答案：C
    解析：
    【考情点拨】本题考查了函数的单调性和凹凸性的知识点．【应试指导】因，f(x)>0，故函数单调递增，又f’(x)<0，所以函数曲线为凸的.

  • 第17题：

    曲线y=xarctanx的凹区间为（）

    A.(0，+)
    B.(-，0)
    C.(-，+)
    D.不存在

    答案：C
    解析：
    【考情点拨】本题考查了曲线的凹区件的知识点．

  • 第18题：

    设函数y(x)是微分方程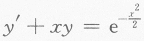满足条件y(0)=0的特解.
    　　(Ⅰ)求y(x)；
    　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.


    答案：
    解析：

  • 第19题：

    设f（x）为区间[a，b]上的连续函数，则曲线y=f（x）与直线x=a，x=b，y=0所围成的封闭图形的面积为（ ）.《》（ ）


    答案：B
    解析：
    本题考查的知识点为定积分的几何意义.由定积分的几何意义可知应选B.常见的错误是选C.如果画个草图，则可以避免这类错误.

  • 第20题：

    在坐标系上，如果表达式是隐函封城（x，y）=0，要绘制这样的函数曲线，下面的描述，那个是合理的（）

    • A、直接通过“任意函数曲线”方式
    • B、将隐函封城f（x， y）=0转为：y=f（x）或x=f（y），然后再绘制函数曲线
    • C、直接通过“带参数的一般曲线”方式，即参变量函数曲线
    • D、直接通过“参数方程曲线”方式

    正确答案:B

  • 第21题：

    曲线y=2x+（8/x）在区间（0，2）内是（）。

    • A、单调增加、凸的
    • B、单调减少、凸的
    • C、单调增加、凹的
    • D、单调减少、凹的

    正确答案:D

  • 第22题：

    单选题
    （2012）当a区间（a，b）内，函数y=f（x）图形沿x轴正向是：（）
    A

    单调减且凸的

    B

    单调减且凹的

    C

    单调增且凸的

    D

    单调增且凹的


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    已知函数y＝y（x）在任意点x处的增量Δy＝yΔx/（1＋x2）＋a，且当Δx→0时，a是Δx的高阶无穷小，y（0）＝π，则y（1）等于（　　）。
    A

    2π

    B

    π

    C

    eπ/4

    D

    πeπ/4


    正确答案： C
    解析：
    由题意可知，dy＝[y/（1＋x2）]dx，分离变量积分得ln|y|＝arctanx＋c。又y（0）＝π得c＝lnπ，故y＝earctanx＋lnπ＝πearctanx，则y（1）＝πeπ/4。

相关内容