曲线y=e^x－e^－x的凹区间是()A、(-∞,0)B、(0,+∞)C、(-∞,1)D、(-∞,+∞)
题目
曲线y=e^x－e^－x的凹区间是()
A、(-∞,0)
B、(0,+∞)
C、(-∞,1)
D、(-∞,+∞)
相似考题
更多“曲线y=e^x－e^－x的凹区间是() ”相关问题
-
第1题：
设函数y(x)是微分方程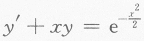
满足条件y(0)=0的特解.
(Ⅰ)求y(x)；
(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.答案：解析：
-
第2题：
【判断题】若函数ƒ（x)在区间I的范围上是凸（凹）的，则-ƒ（x)在区间I内是凹（凸）。（）
A．Y.是
B．N.否
（1）f（x）是凹函数，证明如下： ?x 1 ，x 2 ∈（0，+∞），∵ 1 2 [f( x 1 )+f( x 2 )] = 1 2 ( 3 x 1 + 3 x 2 ) ≥ 3 x 1 x 2 ≥ 3 x 1 + x 2 2 = f( x 1 + x 2 2 ) ∴ f( x 1 + x 2 2 )≤ 1 2 [f( x 1 )+f( x 2 )] ， ∴ f(x)= 3 x (x＞0) 是凹函数 （2）∵函数f 2 （x）=x|ax-3|= a x 2 -3x ax≥3 -a x 2 +3x ax＜3 结合二次函数的图象，要想使函数f 2 （x）为区间[3，6]上的凹函数，需a＜0或 a＞0 3 a ≤3 ∴a的取值范围为（-∞，0）∪[1，+∞） （3）证明：设?x 1 ，x 2 ∈R f 3 ( x 1 )+ f 3 ( x 2 )= f 3 ( x 1 2 + x 1 2 )+ f 3 ( x 2 2 + x 2 2 ) = f 3 2 ( x 1 2 )+ f 3 2 ( x 2 2 )≥2 f 3 ( x 1 2 )? f 3 ( x 2 2 )=2 f 3 ( x 1 + x 2 2 ) 即 f 3 ( x 1 )+ f 3 ( x 2 ) 2 ≥ f 3 ( x 1 + x 2 2 ) 故f 3 （x）为R上的凹函数 -
第3题：
20、若X与Y相互独立，则E（[X-E（X)][Y-E（Y)])=0成立.
P(X+Y>1)=0.5 -
第4题：
1、关于协方差，下列说法正确的是
A．cov(X,Y)=E{[X-E(X)][Y-E(Y)]}
B．cov(X,Y)=E{[X-E(X)]Y}
C．cov(X,Y)=E(XY)-E(X)E(Y)
D．cov(X,Y)=E(XY)+E(X)E(Y)
ABD -
第5题：
若X与Y相互独立，则E（[X-E（X)][Y-E（Y)])=0成立.
D