某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6.5万元的净收益，净残值为6.5万元。若基准收益率为20％，己知：（P/A，20％，20）=4.8696，（P／F，20％，21）=0.0217，则该方案的净现值是（ ）万元。A.2.57B.3.23C.3.52D.4.35

题目

某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6.5万元的净收益，净残值为6.5万元。若基准收益率为20％，己知：（P/A，20％，20）=4.8696，（P／F，20％，21）=0.0217，则该方案的净现值是（ ）万元。

A.2.57

B.3.23

C.3.52

D.4.35

相似考题

1.现有两个互斥的投资方案A和B：A方案现时点投资25万元，此后从第一年年末开始，将有6万元的净收益，寿命期为20年，净残值为7.5万元；B方案现时点的投资额为17.5万元，年净收益为4万元，寿命期也为20年，净残值为6万元。若基准收益率为20%，则折算成现值A方案较B方案多得( )元。已知：(P/A，20%，20)-4.8696，(P/F，20%，20)-0.02608aA.22783 B.24567 C.26456 D.34225

2.某方案现时点投资30万元，1年后开始收益，连续20年，每年将有8万元的净收益，净残值为6万元。若基准收益率为20%，已知(P/A，20%，20)=4.8696，(P/F，20%，20)=0.0261，则该方案的净现值是( )万元。A.2.96 B.8.96 C.9.11 D.14.96

3.某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6．5万元的净收益，净残值为6．5万元。若基准收益率为20％，则该方案的净现值是（　　）万元。已知：?(P／A，20％，20)=4．8696，(P／F，20％，21)?=0．0217。A.2．57 B.3．23 C.3．52 D.4．35

4.某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6.5万元的净收益，净残值为6.5万元。若基准收益率为20%，己知：(P/A，20%，20)=4.8696，(P/F，20%，21)=0.0217，则该方案的净现值是( )万元。A.2.57 B.3.23 C.3.52 D.4.35

参考答案和解析
正确答案：C
[答案]C
[解析]：
把每年净收益折为第2年初现值P1=A（P/A，20%，20）=6.5×4.8696=31.6524
把每年净收益折为现值P2=P1/（1+r）=31.6524/120%=26.377
把净残值折为现值P3=F（P／F，20％，21）=6.5×0.0217=0.14105
所以，净现值=26.377+0.14105-23=3.52
[试题点评]：本题考核的是净现值的求法。参见教材P23
更多“某方案现时点投资23万元,此后从第2年年末开始,连续20年,每年将有6.5万元的净收益,净残值为6.5万 ”相关问题

  • 第1题：

    现有两个互斥的投资方案A和B。A方案现时点投资25万元，此后从第一年年末开始，将有6万元的净收益，寿命期为20年，净残值为7.5万元；B方案现时点的投资额为17.5万元，年净收益为4万元，寿命期也为20年，净残值为6万元。若基准收益率为20%，则折算成现值A方案较B方案多得()元。[已知：(P/A，20%，20)=4.8696，(P/F,20%，20)=0.02608]

    A:34225
    B:22783
    C:24567
    D:26456

    答案：B
    解析：
    方案A的现值为P1=6*(P/A，20%，20)+7.5*(P/F，20%，20)-25=6*4.8696+7.5*0.02608-25=4.4132（万元）；方案B的现值P2=4*(P/A，20%，20)+6*(P/F,20%,20)-17.5=4*4.8696+6*0.02608-17.5=2.1349（万元），P1-P2=44132-21349=22783（元）。

  • 第2题：

    某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6.5万元的净收益，净残值为6.5万元。若基准收益率为20%，己知：(P/A，20%，20)=4.8696，(P／F，20%，21)=0.0217，则该方案的净现值是（　　）万元。
    　
    A．2.57
    B．3.23
    C．3.52
    D．4.35


    答案：C
    解析：
    把每年净收益折为第2年初现值P1=A（P/A,20%,20）=6.5×4.8696=31.6524
    　　把每年净收益折为现值P2=P1/(1+r)=31.6524/120%=26.377
    　　把净残值折为现值P3=F(P／F，20%，21)=6.5×0.0217=0.14105
    　　所以，净现值=26.377+0.14105-23=3.52
    　　试题点评：本题考核的是净现值的求法。参见教材P23。

  • 第3题：

    某方案初始投资23万元，第2年年末开始收益，连续20年每年年末收益均为6．5万元，第21年年末净残值为6．5万元。若基准收益率为20％，则该方案的净现值为( )万元。已知：(P／A，20％，20)=4．8696，(P／F，20％，21)=0．0217。??

    A.2．57
    B.3．23
    C.3．52
    D.4．35

    答案：C
    解析：
    此题考查净现值的计算。净现值是指投资项目按预定的基准收益率，分别将计算期内各年净现金流量折现到投资起点的现值之和。根据题意，该题中现金流量有三部分：
    ①初始投资23万元，折算为现值为-23万元。
    ②第二年年末开始收益，连续20年，每年年末收益均为6．5万元，则需要将连续20年的收益先折算到第一年年末的现值P1，再将P1折算到初始起点，列式为6．5×(P／A，20％，20)÷(1+20％)=6．5×4．8696÷1．2=26．377(万元)。
    ③第21年年末净残值为6．5万元，将其折算为现值为6．5×(P／F，20％，21)=6．5×0．0217=0．14105(万元)。故该方案的净现值=-23+26．377+0．14105=3．52(万元)。

  • 第4题：

    某方案现时点投资23万元，此后从第2年年末开始，连续20年，每年将有6.5万元的净收益，净残值为6.5万元。若基准收益率为20%，己知：（P/A，20%，20）=4.8696，(P/F，20%，21)=0.0217，则该方案的净现值是()万元。

    A:2.57
    B:3.23
    C:3.52
    D:4.35

    答案：C
    解析：
    利用净现值法，把每年净收益折为第2年初现值P1=A（P/A,20%，20）=6.5*4.8696=31.6524；把每年净收益折为第2年初现值P2=P2/(1+r)=31.6524/120%=26.377；把净残值折为第2年初现值P3=F(P/F,20%，21)=6.5*0.0217=0.14105。所以，净现值=26.377+0.14105-23=3.52（万元）。

  • 第5题：

    某方案现时点投资23万元，此后从第二年年末开始，连续20年，每年将有6．5万元的净收益，净残值为6．5万元。若基准收益率为20％，则该方案的净现值是（）万元。已知：(P／A，20％，20)=4．869 6，(P／F，20％，21)=0．021 7。

    A.2．57
    B.3．23
    C.3．52
    D.4．35

    答案：C
    解析：
    ①先画现金流量图。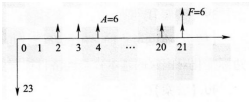
    ②把每年净收益A=6．5万元折为第二年年初第
    一年年末现值。此处为A→P的转换，每年的净收益
    6．5万元是年值A，是从第二年年末开始的，折现后，P值在第一个A值的前一时间点1上，即：第一年年末、第二年年初。
    P1=A(P/A，20％，20)=6．5×4．869 6=31．652 4(万元)。
    ③把时间点1上的净收益继续折为0点位置上的现值(此处为F—P的转换)：
    P2=P1÷(1+r)=31．652 4÷120％=26．377(万元)。
    ④把净残值折为现值(F→P)：
    P3=F(P／F，20％，21)=6．5×0．021 7=0．141 05(万元)。
    所以，净现值=26．377+0．141 05—23=3．52(万元)。
    即：PW=6．5(P/A，20％，20)(P／F，20％，1)+6．5(P／F，20％，21)-23=3．52(万元)。
    常见错误分析：
    ①将20年收益折现时，忘记只折在第一年年末，还需要再折算一次，折到O点位置。
    ②忘记残值也需要折现。
    ③忘记最后减去初始投资23万元。

相关内容