为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差口为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平α=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。A.提出假设H0:μ≤100;H1:μ>100B.提出假设H0:μ≥100;H1:μ<100C.检验统计量及所服从的概率分布为D.如果Z>Zα,则称与μ0的差异是显著的,这时拒绝H
题目
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差口为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平α=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。
A.提出假设H0:μ≤100;H1:μ>100
B.提出假设H0:μ≥100;H1:μ<100
C.检验统计量及所服从的概率分布为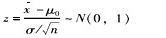
D.如果Z>Zα,则称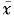 与μ0的差异是显著的,这时拒绝H0
与μ0的差异是显著的,这时拒绝H0
E.检验结果认为该类型的电子元件的使用寿命确实有显著提高
相似考题
更多“ 为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差口为10小时。现在随机抽取100个该类型的电子元件,测得平”相关问题
-
第1题:
某种元件使用寿命X~N(μ,10^2).按照客户要求该元件使用寿命不能低于1000h,现从该批产品中随机抽取25件,其平均使用寿命为x=995,在显著性水平α=0.05下确定该批产品是否合格?答案:解析:令H0:μ≥1 000,H1小于1 000.因为总体方差已知,所以选取统计量 ~N(o,1),
~N(o,1),
左临界点为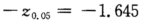 ,因为
,因为 =-2.5小于-1.645,所以拒绝H0,即该批产品不合格.
=-2.5小于-1.645,所以拒绝H0,即该批产品不合格. -
第2题:
(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:
已知产品的使用寿命服从正态分布,样本方差为S2,样本均值为 ,则生产线上该种产品平均使用寿命95%的置信区间为( )。
(注:Z0.025=1.96,t0.025(4)=2.776)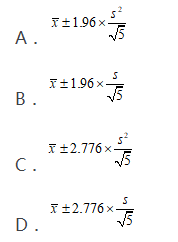 答案:D解析:
答案:D解析: -
第3题:
假定某门学科的测验成绩分布为正态分布,从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 该学区所有考生平均成绩的99%的罝信区间是A.73.20-74.80
B.72.04-75.96
C.72.36-75.64
D.71.42-76.58答案:D解析:计算置信区间,得到74±2.58xl,所以选71.42?6.58。 -
第4题:
某超市想要估平均金额,采取简单随机方式抽取49名顾客进行调查。假定从正态分布,且标准差为15元。如果样本均值为120元求总体均值95%的置信区间。

略 -
第5题:
某灯泡厂家称其灯泡的平均使用寿命在1200小时以上。现从随机抽取25只,得到样本均值为1181.6小时,标准差为45.08小时服从正态分布。根据案例建立适当的原假设和备择假设。
正确答案: 提出假设:
H0:μ≥1200
H1:μ<1200 -
第6题:
在一个饭店门口等待出租车的时间是左偏的,均值为12分钟,标准差为3分钟。如果从该饭店门口随机抽取100名顾客并记录他们等待出租车的时间,则该样本的分布服从()
- A、正态分布,均值为12分钟,标准差为0.3分钟
- B、正态分布,均值为12分钟,标准差为3分钟
- C、左偏分布,均值为12分钟,标准差为3分钟
- D、左偏分布,均值为12分钟,标准差为0.3分钟
正确答案:A -
第7题:
假设某班期末统计学考试成绩服从正态分布,平均成绩为70分,标准差为12分,要求计算: (1)随机抽取1人,该同学成绩在82分以上的概率; (2)随机抽取9人,其平均成绩在82分以上的概率。
正确答案:(1)15.86%, (2)0.135% -
第8题:
有关正态分布表述正确的是()
- A、正态分布的概率可以采用函数Fdist()计算
- B、正态分布的密度曲线图与二项分布相似
- C、标准正态分布的平均数为0,标准差为1
- D、正态分布的变量是一种离散型随机变量
正确答案:C -
第9题:
问答题某工厂收到供货方发来的一批电子元件的例子中,共抽取了10件电子元件进行检验,使用样本的方差为S2=8000.56(小时)。试在95%的置信概率下对该批电子元件使用寿命的方差和标准差进行区别。正确答案:解析: -
第10题:
问答题某灯泡厂家称其灯泡的平均使用寿命在1200小时以上。现从随机抽取25只,得到样本均值为1181.6小时,标准差为45.08小时服从正态分布。根据案例建立适当的原假设和备择假设。正确答案: 提出假设:
H0:μ≥1200
H1:μ<1200解析: 暂无解析 -
第11题:
单选题有关正态分布表述正确的是()A正态分布的概率可以采用函数Fdist()计算
B正态分布的密度曲线图与二项分布相似
C标准正态分布的平均数为0,标准差为1
D正态分布的变量是一种离散型随机变量
正确答案: A解析: 暂无解析 -
第12题:
单选题研究发现,在某银行等待取款的时间分布是左偏的,且均值为15分钟,标准差为5分钟。如果从中随机抽取100名等待取款的顾客,并记录他们等待的时间,则该样本的平均等待时间服从()A近似正态分布,均值为15分钟,标准差为0.5分钟
B近似正态分布,均值为15分钟,标准差为5分钟
C仍为左偏分布,均值为15分钟,标准差为5分钟
D仍为左偏分布,均值为15分钟,标准差为0.5分钟
正确答案: C解析: 等待取款的时间分布是左偏的,且均值为15分钟,标准差为5分钟。则其平均等待时间近似正态分布,且均值为15分钟,标准差为0.5分钟。 -
第13题:
若随机变量ξ服从正态分布,ξ~N(0,2),则该正态分布的均方差为( )。A、0
B、20.5
C、2
D、4答案:C解析: -
第14题:
为了考察某种类型的电子元件的使用寿命情况,假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为:平均使用寿命μ0为100小时,标准差a为10小时。现在随机抽取100个该类型的电子元件,测得平均寿命为102小时,给定显著性水平a=0.05,为了判断该电子元件的使用寿命是否有明显的提高,下列说法正确的有( )。
 答案:A,C,D,E解析:
答案:A,C,D,E解析:
-
第15题:
假定某门学科的测验成绩分布为正态分布,从某一学区随机抽取的65名考生的 平均分为74,标准差为8。 根据本次测验成绩,该测验分数的平均数的标准误 答案:A解析:题考察的是标准误的计算公式,总体正态,方差未知,则标准为
答案:A解析:题考察的是标准误的计算公式,总体正态,方差未知,则标准为
-
第16题:
某灯泡厂家称平均使用寿命在1100小时以上随机抽取25只,测得其平均寿命为991小时,标准差为39.02小时。服从正态分布,取显著性水平为0.01,厂家的说法是否成立。

略 -
第17题:
某食品公司开发了一种新食品,为了验证消费者对该食品是否喜爱,公司组织了一次市场调研,共调研了400名消防者,其中358名观众喜爱该产品,问喜爱该产品的消费者服从()
- A、均值是200,标准差为20的正态分布
- B、均值是200,标准差为10的正态分布
- C、均值是200,标准差为100的正态分布
- D、其他分布
正确答案:B -
第18题:
某电子元件厂某月生产电子管10000个,采用随机抽样检验产品的平均使用寿命和产品合格率,样本容量为180个,检验结果180个电子管的平均使用寿命为3880小时,产品合格数为174个。要求推断该批电子管的平均使用寿命、产品合格率和总合格品数。
正确答案: 推断该批电子管的平均使用寿命:3880小时
产品合格率:174/180*100=96.66%
总合格品数:1000*96.66%=9666(个) -
第19题:
电子元件厂日产10000只元件,经多次一般测试得知一等品率为92%,现拟采用随机抽样方式进行抽检,如果求误差范围在2%之内,可靠程度为95.45%,需抽取()电子元件。
正确答案:686 -
第20题:
研究发现,在某银行等待取款的时间分布是左偏的,且均值为15分钟,标准差为5分钟。如果从中随机抽取100名等待取款的顾客,并记录他们等待的时间,则该样本的平均等待时间服从()
- A、近似正态分布,均值为15分钟,标准差为0.5分钟
- B、近似正态分布,均值为15分钟,标准差为5分钟
- C、仍为左偏分布,均值为15分钟,标准差为5分钟
- D、仍为左偏分布,均值为15分钟,标准差为0.5分钟
正确答案:A -
第21题:
问答题40.已知某种类型电子元件的寿命X(单位:小时)服从指数分布,它的概率密度为 一台仪器装有4个此种类型的电子元件,其中任意一个损坏时仪器便不能正常工作.假设4个电子元件损坏与否互相独立. 试求:(1)一个此种类型电子元件能工作2 000小时以上的概率p1; (2)一台仪器能正常工作2 000小时以上的概率p2.正确答案:解析: -
第22题:
单选题总体不呈正态分布,从该总体中随机抽取容量为1000的一切可能样本的平均数的分布接近于:()A二项分布
BF分布
Ct分布
D正态分布
正确答案: C解析: 暂无解析 -
第23题:
多选题(二)质检人员从生产线上随机抽取5件产品检验其使用寿命,产品的质量标准是使用寿命不小于100小时。5件产品的使用寿命(单位:小时)分别为125、100、115、90、125。请根据上述资料回答下列问题:5件产品的使用寿命( )。A中位数为115
B算术平均数为111
C呈左偏态分布
D呈右偏态分布
正确答案: C,B解析:


