对某天生产的2000件电子元件的耐用时间进行全面检测,又抽取5%进行抽样复测,资料如表5-1所示。规定耐用时间在3000小时以下为不合格品,则该电子元件合格率的抽样平均误差为 ( )。A.1.63%B.1.54%C.1.52%D.1.35%
题目
对某天生产的2000件电子元件的耐用时间进行全面检测,又抽取5%进行抽样复测,资料如表5-1所示。

规定耐用时间在3000小时以下为不合格品,则该电子元件合格率的抽样平均误差为 ( )。
A.1.63%
B.1.54%
C.1.52%
D.1.35%
相似考题
更多“ 对某天生产的2000件电子元件的耐用时间进行全面检测,又抽取5%进行抽样复测,资料如表5-1所示。规定耐用时间在3000小时以下为不合格品,则该电子元件合格率的抽样平均误差为 ( )。A.1.63%B.1.54%”相关问题
-
第1题:
某电子元件厂在2009年9月份大量生产某种型号的电子元件,现采用随机抽样调查方式,进行质量检测,检测结果如表5-3所示。
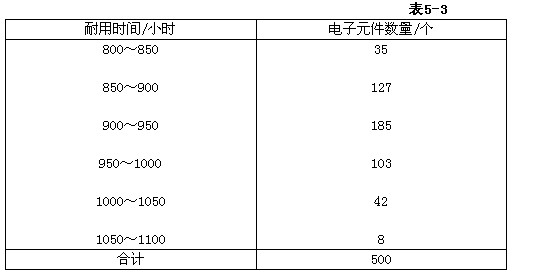
根据上述资料请回答:
样本标准差的计算公式和数值分别为( )。
 正确答案:BD
正确答案:BD
解析:这是根据分组资料计算样本标准差,所以 -
第2题:
对10000只灯泡进行耐用性能测试,根据以往资料,耐用时间标准差为51.91小时,若采用重复抽样方法,概率保证68.27%,平均耐用时数的误差范围不超过9小时。在这种条件下应抽取34只灯泡进行耐用性能测试。
A.正确
B.错误
正确答案:A
-
第3题:
某经销商采用GB/T2828. 1对某类袋装食品进行抽样验收,规定N= 150,检验水平为S-2,AQL=6. 5(%)。
用二次正常抽样方案抽取第一个样本,若其中的不合格品数为d =2,则( )。
A.接收该批产品
B.不接收该批产品
C.再抽样取第二个样本进行检验,若d2=0,则接收该批产品
D.再抽样取第二个样本进行检验,若d2=1,则拒收该批产品答案:B解析:对批接收性的判定规则要求:若d小于等于接收数Ac,则接收该批;若d大于等于拒收数Re,则不接收该批。二次抽样的两个方案接收性分别为:①若按方案(n,Ac) = (2, 0),则d=2>Re = Ac +1 =1,故应拒收该批产品;②若按方案n1=n2 =5,判定组数为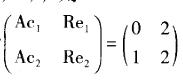 ,则第一次抽样不合格品数d1=2 = Re1=2,故应拒收该批产品
,则第一次抽样不合格品数d1=2 = Re1=2,故应拒收该批产品 -
第4题:
从N=100的总体中随机抽取10%的样本进行调查,可能组成的不同样本数在( )。A.重复抽样下为10
B.重复抽样下为
C.不重复抽样下为10
D.不重复抽样下为答案:D解析: -
第5题:
利用GB/T 2828.1进行抽样验收,规定N= 150,检验水平为S—2,AQL=6. 5 (%)。(提供抽样检验用附表)求得:
若用二次正常抽样方案,抽取第一个样本,若其中的不合格品数为d=2,则( )。
A.接收该批产品
B.拒收该批产品
C.再抽样取第二个样本进行检验若d2=0,则接收该批产品
D.再抽样取第二个样本进行检验若尖d2=1,则接收该批产品答案:B解析:
-
第6题:
采用简单重复抽样的方法,抽取一批产品中的200件作为样本,其中合格品为195件。以95.45%的概率保证程度对该产品的合格率进行区间估计【z=2】。
抽样极限误差:△p=Zμ=2×1.1%=2.2%,则合格率的范围:P=p±△p=97.5%±2.2% 即95.3%≤P≤99.7%样本的抽样平均误差为1.1%,在95.45%的概率保证程度下,该批产品合格率在95.3%至99.7%之间。
略 -
第7题:
某企业生产一批袋装食品,共2000袋,按简单随机不重复抽样方式,抽取100袋检查其净重量是否合格,结果发现不合格率为5%,不合格率的抽样平均误差是()。
- A、2.18%
- B、2.12%
- C、0.5%
- D、0.48%
正确答案:B -
第8题:
在进行纯随机重复抽样时,为使抽样平均误差减少25%,则抽样单位数应()。
- A、增加25%
- B、增加78%
- C、增加1.78%
- D、减少25%
正确答案:B -
第9题:
采用简单随机抽样的方法,从2000件产品中抽查200件,其中合格品190件,要求: (1)计算合格品率及其抽样平均误差。 (2)以95.45%概率保证程度,对合格品率和合格品数量进行区间估计。 (3)如果合格品率的极限误差为2.31%,则其概率保证程度是多少?
正确答案:(1)合格品率为95%,抽样平均误差为1.54%,
(2)合格率估计:(91.92%,98.08%)合格品数估计:(1838,1962)
(3)概率保证程度为86.64% -
第10题:
电子元件厂日产10000只元件,经多次一般测试得知一等品率为92%,现拟采用随机抽样方式进行抽检,如果求误差范围在2%之内,可靠程度为95.45%,需抽取()电子元件。
正确答案:686 -
第11题:
单选题以下关于钢结构安装中的焊缝检测数量说法正确的是()。A对各种焊接方法和焊接位置的焊缝抽样检测数量不小于5%
B对各种焊接方法的坡口焊缝重点进行抽样检测,抽样检测数量不小于20%
C对管道对接全熔透焊缝重点进行抽样检测,抽样检测数量不小于20%
D弯曲抽样检测在主要构件上逐批抽取2%进行打弯检验
正确答案: B解析: 暂无解析 -
第12题:
问答题采用简单重复抽样的方法,抽取一批产品中的200件作为样本,其中合格品为195件。以95.45%的概率保证程度对该产品的合格率进行区间估计【z=2】。正确答案: 抽样极限误差:△p=Zμ=2×1.1%=2.2%,则合格率的范围:P=p±△p=97.5%±2.2% 即95.3%≤P≤99.7%样本的抽样平均误差为1.1%,在95.45%的概率保证程度下,该批产品合格率在95.3%至99.7%之间。解析: 暂无解析 -
第13题:
重复抽样条件下,耐用时间的抽样平均误差计算公式和数值分别为( )。
 正确答案:ABC
正确答案:ABC
解析:重复抽样条件下,抽样平均误差,总体方差未知时,可用样本统计量来估计,那么 -
第14题:
在根据检索要素规定的抽样方案抽取样本,发现样本中不合格品数量大于接收数,则( )。
A.接收该批产品
B.不接受该批产品
C.利用二次抽样再进行判断
D.无法判断该批产品是否接收
正确答案:B
-
第15题:
小明在一家超市工作,该超市将进行整体改造,小明负责信息系统软硬件升级,他制定的工作计划如表5-1所示。表5-1每项任务持续时间表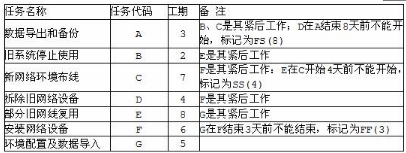
每项任务的逻辑关系和部分时间信息如图5-1所示。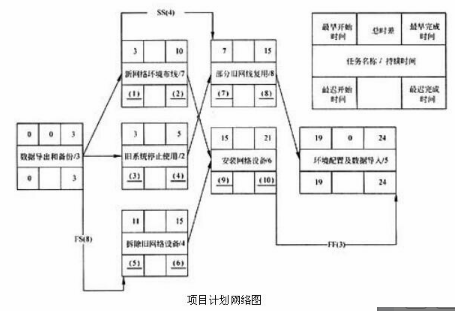
请根据表5-1和图5-1,计算各项任务的最迟开始时间和最迟结束时间,填充图5-1中的空38~39。计算下表中每项任务的总时差,填充其中的空49~48。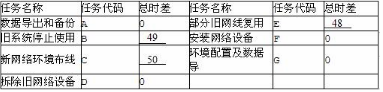
写出该项目的关键路径(在答题纸对应位置填写任务代码)。A-51-52-G答案:解析:38、7 39、 14 40、9 41、 11 42、 11
43、 15 44、 11 45、 19 46、 15 47、 2148、6 49、4 50、4 51、D 52、F
38-47、[解析] 本题考查项目管理中网络图、关键路径及相关计算。项目计划网络图中时间参数的计算应在确定各项工作的持续时间之后进行。1.最早开始和最早完成时间ES、EF。计划网络图中各项工作的最早开始时间和最早完成时间的计算应从网络计划的起始结点开始,顺着箭线方向依次逐项计算。1)起始结点的最早开始时间为零。2)工作的最早开始时间等于该工作的各个紧前工作的最早完成时间的最大值,即ES=max{紧前工作的EF};3)工作的最早完成时间等于该工作的最早开始时间加上其持续时间,即EF=ES+本工作持续时间;2.最迟开始时间和最迟完成时间LS、LF。网络计划中各项工作的最迟开始时间和最迟完成时间的计算应以项目规定或计算的I期为基准,从网络计划的终止结点,逆着箭线方向依次逐项计算。1)最迟结束时间:某工作的最迟结束时间等于该工作的各项紧后工作的最迟开始时间的最小值,即LF=min{紧后工作的LS};2)最迟开始时间:本项工作的最迟结束时间减本项工作的持续时间,即LS=LF-工作的持续时间;3.工作的总时差TF:工作的总时差指在不影响整个项目最早完成时间的前提下,各项工作的完工期可以推延的时间。工作总时差等于该工作最迟完成时间与最早完成时间之差,或该工作最迟开始时间与最早开始时间之差,即TF=LF-EF,或TF=LS-ES;4.工作的自由时差FF:工作自由时差指在不影响紧后工作的最早开始时间的前提下,一项工作的完工期可以推延的时间。自由时差的计算应按以下两种情况分别考虑:1)对于有紧后工作的工作,其自由时差等于本工作之紧后工作最早开始时间减本工作最早完成时间所得之差的最小值,即FF=min{ES(紧后工作)}-EF;2)对于无紧后工作的工作,也就是以网络计划终点结点为完成结点的工作,其自由时差等于计划工期与本工作最早完成时间之差。需要指出的是,对于网络中以终点结点为完成结点的工作,其自由时差与总时差相等。此外,由于工作的自由时差是其总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零,可不必进行专门计算。在实际项目中,可能会出现其他情况。例如,紧后工作和紧前工作具有一定的平行特性,即紧后工作的开始并不以紧前工作的结束为前提,紧后工作只需在紧前工作开始一段时间后即可开始,将这样工作间的平行关系称为搭接关系。一般将这样的搭接关系分成四类:(1)结束—开始型(finish-to-start):B在A结束T时间之前不能开始,标记为FS (T)如下图(a)所示。(2)结束—结束型(finish-to-finish,FF):B在A结束T时间之前不能结束,标记为FF (T)如下图(b)所示。(3)开始—开始型(start-to-start,SS):B在A开始T时间之前不能开始,标记为SS (T)如下图(c)所示。(4)开始—结束型(start-to-finish,SF):B在A开始T时间之前不能结束,标记为SF (T)如下图(d)所示。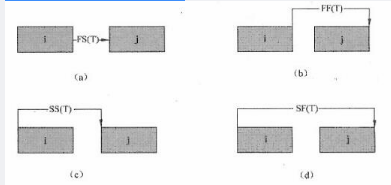
具体计算如下:(1)结束—开始型(finish-to-start,FS(T)):B在A结束T时间之前不能开始,标记为FS(T),T表示时间间隔,各参数计算规则如下:最早时间:ESj=EFi+FS (T)最迟时间:LFi=LSj-FS(T)自由时差:FFi=ESj-FS(T)-EFi(2)结束—结束型(FF):B在A结束T时间之前不能结束,标记为FS(T),T表示时间间隔,各参数计算规则如下:最早时间:EFj=EFi+FF (T)最迟时间:LFi=LFj-FF (T)自由时差:FFi=EFj-FF (T)-EFi(3)开始—开始型(SS):B在A开始T时间之前不能开始,标记为FS(T),T表示时间间隔,各参数计算规则如下:最早时间:ESj=ESi+SS (T)最迟时间:LSi=LSj-SS (T)自由时差:FFi=ESj-SS (T)-ESi(4)开始—结束型(SF):B在A开始T时间之前不能结束,标记为FS(T),T表示时间间隔,各参数计算规则如下:最早时间:EFj=ESi+SF (T)最迟时间:LSi=LFj-SF (T)自由时差:FFi=EFj-SF (T)-ESi这四类情况下,总时差的计算规则与一般网络相同。根据上述公式,问题1计算结果如下: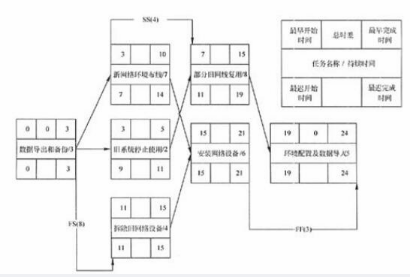
48-50、[解析] 计算结果如下:
51-52、[解析] 计算结果如下:总时差最小的工作为关键工作,由关键工作构成的线路为关键线路或关键路径。本项目中从开始结点到最终结点间,A、D、F、G工作的总时差均为O,故本项目的关键路径是A-D-F-G。 -
第16题:
对批量构件的钢筋保护层厚度进行验收检查,第一次检测的合格率为82%,以下叙述正确的是( )。A、该批构件的钢筋保护层厚度不合格
B、可抽取相同数量的构件进行复检
C、可抽取双倍数量的构件进行复检
D、当按两次抽样总和计算的合格率为90%及以上时,可判定合格
E、当按两次抽样总和计算的合格率为85%及以上时,可判定合格答案:B,D解析:《混凝土结构工程施工质量验收规范》(GB50204-2015)附录E:“结构实体钢筋保护层厚度检验”:
(1)当全部钢筋保护层厚度检验的合格率为90%及以上时,可判为合格;
(2)当全部钢筋保护层厚度检验的合格率小于90%但不小于80%时,可再抽取相同数量的构件进行检验;当按两次抽样总和计算的合格率为90%及以上时,仍可判定为合格;
(3)每次抽检不合格点的最大偏差不应大于允许偏差的1.5倍。 -
第17题:
某企业生产某种产品,品种单一,批量大,生产相对稳定。利用抽样检验对产品 进行验收,则:
若根据检索要素确定的抽样方案抽取样本,发现样本中不合格品数d大于接收数 Ac,则( )。
A.接收该批产品
B.不接收该批产品
C.利用二次抽样再行判断
D.无法判断该批产品是否接收答案:B解析: -
第18题:
以下关于钢结构安装中的焊缝检测数量说法正确的是()。
- A、对各种焊接方法和焊接位置的焊缝抽样检测数量不小于5%
- B、对各种焊接方法的坡口焊缝重点进行抽样检测,抽样检测数量不小于20%
- C、对管道对接全熔透焊缝重点进行抽样检测,抽样检测数量不小于20%
- D、弯曲抽样检测在主要构件上逐批抽取2%进行打弯检验
正确答案:D -
第19题:
某电子元件厂某月生产电子管10000个,采用随机抽样检验产品的平均使用寿命和产品合格率,样本容量为180个,检验结果180个电子管的平均使用寿命为3880小时,产品合格数为174个。要求推断该批电子管的平均使用寿命、产品合格率和总合格品数。
正确答案: 推断该批电子管的平均使用寿命:3880小时
产品合格率:174/180*100=96.66%
总合格品数:1000*96.66%=9666(个) -
第20题:
某商店对新购进的一批商品实行简单随机抽样检查,抽样后经计算得:该商品的合格率为98%,抽样平均误差为1%,试在如下条件下分别估计该批商品的合格率: 若给定极限误差为2%。
正确答案: 在极限误差为2%时,该批商品的合格率为[96.04%,99.96%],保证程度为95.45%。 -
第21题:
从一批产品中随机抽取100件进行质量检验,结果有5件不合格,则样本成数的抽样平均误差为0.689。
正确答案:错误 -
第22题:
单选题某灯泡厂对一定时期内生产的某种型号的灯泡进行质量检验,采用简单随机重复抽样的调查方式,得到下表资料: 根据上述资料请回答: 每个灯泡的耐用时间是()。A时点指标
B时期指标
C数量标志
D品质标志
正确答案: C解析: 暂无解析 -
第23题:
问答题某工厂收到供货方发来的一批电子元件的例子中,共抽取了10件电子元件进行检验,使用样本的方差为S2=8000.56(小时)。试在95%的置信概率下对该批电子元件使用寿命的方差和标准差进行区别。正确答案:解析:
