设备的维修时间X服从指数分布，则随机变量X可能取值的范围为（ ）。 A. ( - ∞ , +∞ ) B. [0, + ∞ ) C. ( - ∞ , 0] D. [0, 1 ]

题目
设备的维修时间X服从指数分布，则随机变量X可能取值的范围为（ ）。
A. ( - ∞ , +∞ ) B. [0, + ∞ ) C. ( - ∞ , 0] D. [0, 1 ]

相似考题

1.离散型随机变量X,X所有取值为0,1,2,且P(X=0)=0.5,P(X=1)=0.25,P(X=2)=0.25,则P(X3)=()A、0B、0.5C、0.25D、1

2.设服从N(0,1)分布的随机变量X，其分布函数为Φ(x)。如果Φ(1) = 0.84，则P{ X ≤1}的值是： A. 0. 25 B. 0. 68 C. 0. 13 D. 0. 20

3.—次电话的通话时间X是一个随机变量（单位：分），设X服从指数分布Exp (λ),其中λ= 0.25,则一次通话所用的平均时间E (X)与标准差σ(X)为( )。 A. E (X) =2 B. E (X) =4 C.σ（X）=4 D.σ (X) =16 E. E (X) =0. 25

4.设备的维修时间X服从指数分布，则随机变量X可能取值的范围为( )。A．(-∞，+∞)B．[0，+∞)C．(-∞，0]D．[0，1]

参考答案和解析
答案：B
解析：
服从指数分布的随机变量X仅取非负实数，即仅在[0，∞)上取值。
更多“设备的维修时间X服从指数分布，则随机变量X可能取值的范围为（ ）。 A. ( - ∞ , +∞ ) B. [0, + ∞ ) C. ( - ∞ , 0] D. [0, 1 ]”相关问题

  • 第1题：

    已知X服从指数分布Exp(λ)，其概率密度函数为：p(x)=λe-λx， λ=0.1的情况下，P(5≤X≤20)=( )。
    A. 0. 1353 B. 0. 4712 C. 0. 6065 D. 0. 7418


    答案：B
    解析：

  • 第2题：

    设随机变量X服从参数为2的指数分布,证明：Y=1-在区间(0,1)上服从均匀分布.


    答案：
    解析：

  • 第3题：

    设服从N(0,1)分布的随机变量X，其分布函数为φ(x)，如果φ(1)=0.84，则P|x|≤1的值是( )。



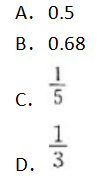    答案：B
    解析：
    X～N(0,1)，P{|x|≤1)=2Φ(1)-1=0.68

  • 第4题：

    若二维随机变量（X，Y）的分布规律为：



    且X与Y相互独立，则α、β取值为（　　）。

    A． α＝1/6，β＝1/6
    B． α＝0，β＝1/3
    C． α＝2/9，β＝1/9
    D． α＝1/9，β＝2/9

    答案：C
    解析：
    由已知表得，边缘分布率为




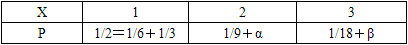
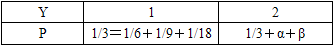
    因为X与Y相互独立，所以P{X＝2，Y＝1}＝P{X＝2}P{Y＝1}，得
    1/9＝（1/9＋α）×1/3
    计算得α＝2/9。同理，P{X＝3，Y＝1}＝P{X＝3}P{Y＝1}，得
    1/18＝（1/18＋β）×1/3
    计算得β＝1/9。

  • 第5题：

    设服从N(0,1)分布的随机变量X,其分布函数为Φ（x）。如果Φ（1）=0.84,则P{ X ≤1}的值是（ ）。


    A. 0.25 B. 0.68 C. 0.13 D. 0.20


    答案：B
    解析：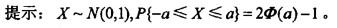

  • 第6题：

    随机变量X服从正态分布，其观测值落在距均值的距离为1倍标准差范围内的概率为（ ）。
    A. 0. 68 B. 0. 95 C. 0. 9973 D. 0.97


    答案：A
    解析：
    答案为A。随机变量X服从正态分布，其观测值落在距均值的距离为1倍标准 差范围内的概率为0.68，其观测值落在距均值的距离为2倍标准差范围内的概率为0.95，其 观测值落在距均值的距离为3倍标准差范围内的概率为0.9973。

  • 第7题：

    设随机变量X服从参数为2的指数分布，则E（2X－1）=（）

    • A、0
    • B、1
    • C、3
    • D、4

    正确答案:A

  • 第8题：

    随机变量X～N（μ,σ2），参数μ和σ的取值范围是（）。

    • A、μ>0,σ>0
    • B、μ>0,-∞<σ<+∞
    • C、-∞<μ<+∞，-∞<σ<+∞
    • D、-∞<μ<+∞，σ>0

    正确答案:D

  • 第9题：

    单选题
    服从指数分布的随机变量X可能取值的范围为(　　)。
    A

    (－∞，+∞)      

    B

    [－0，+∞)    

    C

    (－∞，0)    

    D

    [0，1]


    正确答案： D
    解析： 根据离差平方和的定义可以知道

  • 第10题：

    单选题
    随机变量X～N（μ,σ2），参数μ和σ的取值范围是（）。
    A

    μ>0,σ>0

    B

    μ>0,-∞<σ<+∞

    C

    -∞<μ<+∞，-∞<σ<+∞

    D

    -∞<μ<+∞，σ>0


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。
    A

    1

    B

    3


    正确答案： D
    解析： 暂无解析

  • 第12题：

    填空题
    若随机变量X1，X2，X3相互独立且服从于相同的0-1分布，P{X＝1}＝0.7，P{X＝0}＝0.3，则随机变量Y＝X1＋X2＋X3服从于参数为____的____分布，且E（Y）＝____。D（Y）＝____。

    正确答案： 3,0.7,二项,2.1,0.63
    解析：
    由0-1分布与二项分布之间联系可得Y～B（3，0.7），则E（Y）＝3×0.7＝2.1，D（Y）＝3×0.7（1－0.3）＝0.63。

  • 第13题：

    设x 为随机变量，且 P (X≤10) =0.3，P(X>30) =0.4,则 P (10
    A. 0. 1 B. 0. 2

    C.0. 3 D. 0. 4


    答案：C
    解析：
    。P(1030)=0. 3。

  • 第14题：

    若随机变量X与Y相互独立，且X在区间[0,2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E(XY)等于：


    答案：D
    解析：
    提示X与Y独立时，E(XY)=E(X)E(Y)，X在[a，b]上服从均匀分布时，E(X) =

  • 第15题：

    设随机变量X服从指数分布，其概率密度为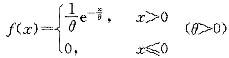 ，则有( )。

    A、E(X)=θ，D(X)=θ2
    B、E(X)=θ2，D(X)=θ
    C、E(X)=0，D(X)=θ
    D、E(X)=0，D(X)=θ2

    答案：A
    解析：
    要记住重要的随机变量的数学期望E(X)和D(X)，对指数分布E(X)=θ，D(X)=θ2

  • 第16题：

    设服从N(0,1)分布的随机变量X，其分布函数为Φ(x)。如果Φ(1) = 0.84，则P{ X ≤1}的值是：

    A. 0. 25
    B. 0. 68
    C. 0. 13
    D. 0. 20

    答案：B
    解析：
    提示：X~N(0,1) ,P{-a≤X≤a}=2Φ(a)-1。

  • 第17题：

    设随机变量X~N(1，32)，则P(X>1)=( )。
    A. 0 B. 0.5
    C. 0. 9 D. 1


    答案：B
    解析：
    。X~N(1，32)，即X为关于1对称的正态分布，因此P(X>1)=0.5。

  • 第18题：

    设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。

    • A、1
    • B、3

    正确答案:D

  • 第19题：

    设X服从0—1分布，P=0.6，Y服从λ=2的泊松分布，且X，Y独立，则X+Y（）.

    • A、服从泊松分布
    • B、仍是离散型随机变量
    • C、为二维随机向量
    • D、取值为0的概率为0

    正确答案:B

  • 第20题：

    设随机变量X服从N（-1，4），则P｛X+1＜0｝=（）


    正确答案:0.5

  • 第21题：

    填空题
    若随机变量X1，X2，X3相互独立且服从于相同的0-1分布P{X=1}=0.7，P{X=0}=0.3，则随机变量P{X=0}=0.3.则随机变量Y=X1+X2+X3服从于参数为____的____分布，且E（Y）=____.D（Y）=____.

    正确答案： 3,0.7,二项,2.1,0.63
    解析： 暂无解析

  • 第22题：

    单选题
    设备的维修时间X服从指数分布，则随机变量X可能取值的范围为（　　）。[2007年真题]
    A

    （-∞，+∞）

    B

    [0，+∞）

    C

    （-∞，0]

    D

    [0，1]


    正确答案： B
    解析：
    服从指数分布的随机变量X仅取非负实数，即仅在[0，∞）上取值。

  • 第23题：

    单选题
    随机变量X～N（μ,σ2），参数μ和σ的取值范围是(　　)。
    A

    μ>0, σ>0  

    B

    μ>0, -∞<σ<+∞  

    C

    -∞<μ<+∞，-∞ <σ<+∞ 

    D

    -∞<μ<+∞，σ>0


    正确答案： D
    解析： 暂无解析

相关内容