—次电话的通话时间X是一个随机变量（单位：分），设X服从指数分布Exp (λ),其中λ= 0.25,则一次通话所用的平均时间E (X)与标准差σ(X)为( )。 A. E (X) =2 B. E (X) =4 C.σ（X）=4 D.σ (X) =16 E. E (X) =0. 25

第1题：

答案：D

解析：

第2题：

设X1，X2，…，Xn，…为独立同分布的随机变量列，且均服从参数为λ(λ>1)的指数分布，记φ(x)为标准正态分布函数，则

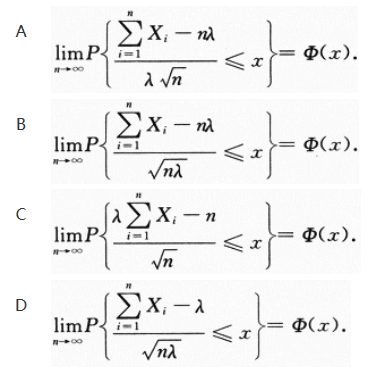答案：C

解析：

【简解】本题是数四的考题.X1，X2，…，Xn，…独立同分布、方差存在.根据中心极限定理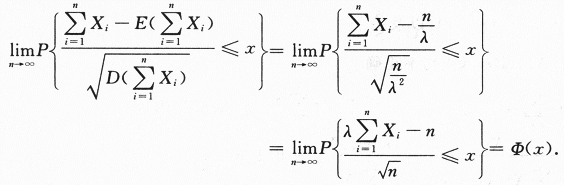　　

第3题：

一次电话通话时间X是一个随机变量（单位：分），X的分布函数为：


当你走进公用电话亭时，恰好有一个人在你前面开始打电话，你的等待时间不超过3分钟的概率是（ ）。
A. e -1 B. 1-e-1 C. 3e-1/3 D. 1 -e-1/3

第4题：

设随机变量X服从参数为A的指数分布,则P{X>)=_______.

答案：

解析：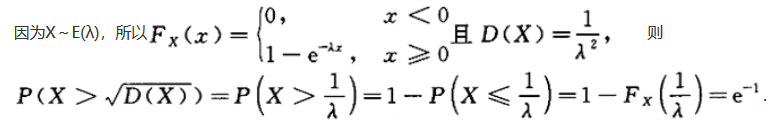

第5题：

设随机变量X服从参数为λ的指数分布，则=_______.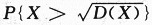

答案：

解析：

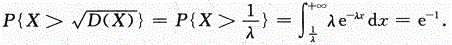答案应填e.

第6题：

设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X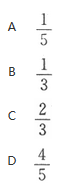

答案：A

解析：

X～E(1)，Y～E(4)且相互独立，所以(X，Y)的概率密度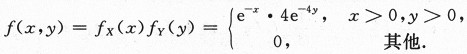　　
　　利用公式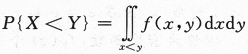可以计算出结果.
　　【求解】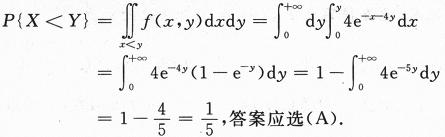

第7题：

第8题：

设随机变量X与Y相互独立，且X在区间［0，2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E（XY）等于（）。

• A、1
• B、3

第9题：

设随机变量X服从参数为3的泊松分布，则E（X-3）=（）

第10题：

设随机变量X与Y相互独立，已知X服从区间（1，5）上的均匀分布，Y服从参数λ=5的指数分布，则D（3X-5Y）等于（）．

• A、5
• B、9
• C、10
• D、13

第11题：

第12题：

第13题：

设随机变量X服从指数分布，其概率密度为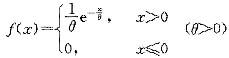 ，则有( )。

A、E(X)=θ，D(X)=θ2
B、E(X)=θ2，D(X)=θ
C、E(X)=0，D(X)=θ
D、E(X)=0，D(X)=θ2

第14题：

设总体X服从参数λ的指数分布，X1，X2，…，Xn是从中抽取的样本，则E(X)为( )。

答案：A

解析：

由于x服从指数分布，即



所以

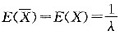
第15题：

第16题：

设随机变量X服从参数为的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).

答案：

解析：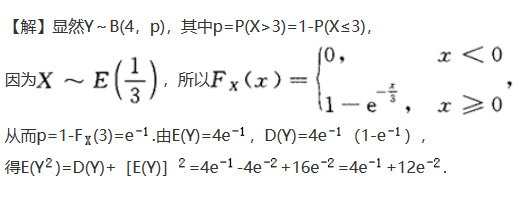

第17题：

答案：

解析：

由随机变量X服从参数为λ的指数分布，得，于是，而，解得λ=.

第18题：

第19题：

设随机变量x服从二项分布b(10，0.9)，则其均值与标准差分别为（）。

• A、E(X)=10
• B、E(X)=9
• C、Vax(X)=0.3
• D、Vax(X)=0.9
• E、Vax(X)=0.3

第20题：

设服从N（0，1）分布的随机变量X，其分布函数为φ（x）。如果φ（1）=0.84，则P{|x|≤1}的值是（）。

• A、0.25
• B、0.68
• C、0.13
• D、0.20

第21题：

设随机变量X服从参数为2的指数分布，则E（2X－1）=（）

• A、0
• B、1
• C、3
• D、4

第22题：

第23题：