某科室共有8人,现在需要抽出两个2人小组到不同的下级单位检查工作,共有多少种不同的安排方案: A420 B840 C210 D260
题目
A420
B840
C210
D260
相似考题
更多“某科室共有8人,现在需要抽出两个2人小组到不同的下级单位检查工作,共有多少种不同的安排方案: ”相关问题
-
第1题:
从五本不同的书中抽出4本,分给两个同学,每人两本,共有多少种分法?( )
A. 11B. 30 C. 60D. 120
【解析】这是一道典型的排列组合题目。元素总个数为5。事件为从5本书中抽出4本分别给两个同学。完成这件事一共需要两个步骤:从5本书中取出4本;把4本书分给两个同学。第一个步骤:从5本书中取出4本,没有排序,是一个组合问题。故完成第一个步骤有C54=5种方法。第二个步骤:把4本书分给两个同学,有顺序,是一个排列问题。故完成第二个步骤有P42=(4×3×2×1)/(2×1)=12种方法。所以完成这件事情一共有5×12=60种方法。所以答案为C
-
第2题:
某办公室共有7个科员,2个副主任,现安排l个副主任带4个科员作出国考察,不同的安排方案共有( )种。
A.70
B.210
C.212
D.420
正确答案:A
-
第3题:
某科室共有8人,现在需要抽出两个2人小组到不同的下级单位检查工作,共有( )种不同的安排方案。A.420
B.840
C.210
D.260答案:A解析:
-
第4题:
7名志愿者中安排6人在周六、周日两天参加社区公益活动.若每天安排3人,则不同的安排方案共有__________种(用数字作答).答案:解析: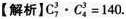
-
第5题:
某单位有两个对口扶贫地,每月需安排10人到两地参与扶贫工作,要求每个对口扶贫地区至少要有4人参与工作。问共有多少种不相同的分配方案?A.210
B.252
C.420
D.672答案:D解析:
-
第6题:
小王等6名学生参与了某展览会志愿者活动。他们被安排到两个不同的会场服务。如果要求每个会场都至少有2名志愿者,则对小王等人共有_________种不同的安排方式。A.20
B.30
C.50
D.360答案:C解析:

-
第7题:
按份共有和共同共有的区别主要体现在()。A.成立的原因不同
B.共有人应尽的义务不同
C.对共有物的管理不同
D.对第三人行使权利不同
E.分割共有物的限制不同答案:A,C,D,E解析:此题考査按份共有和共同共有的区别。区别包括:①成立原因不同;②权利的享有不同;③对共有物的管理不同;④对第三人行使权利不同;⑤分割共有物的限制不同。 -
第8题:
某沿海城市管辖7个县,这7个县的位置如图。现用红、黑、绿、蓝、紫五种颜色给图染色,要求任意相邻的两个县染不同颜色。共有多少种不同的染色方法?()
A. 2400 B. 4860 C. 1920 D. 5760答案:B解析:把该沿海城市地图上的7个县分别编号为A、B、C、D、E、F、G(如图1)。为了便于观察,可以把图1改画成图2(相邻关系不改变)。我们不妨按A、B、C、D、E、F、G的顺序,用红、黑、绿、蓝、紫五种颜色依次染色,根据乘法原理,共有5X4X3X3X3X3X3 = 4860(种)不同的染色方法。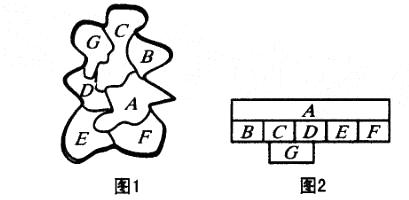
-
第9题:
某科室共有8人,现在需要抽出两个2人的小组到不同的下级单位检查工作,问共有多少种不同的安排方案()
- A、210
- B、260
- C、420
- D、840
正确答案:C -
第10题:
科室共有8人,现在需要抽出两个2人的小组到不同的下级单位检查工作,问共有多少种不同的安排方案?()
- A、210
- B、260
- C、420
- D、840
正确答案:C -
第11题:
单选题科室共有8人,现在需要抽出两个2人的小组到不同的下级单位检查工作,问共有多少种不同的安排方案?()A210
B260
C420
D840
正确答案: C解析: 本题共被作答1次,正确率为0.00%,易错项为B解析解析1分两步解决,对于第一个检查单位先从8人中任意抽出2人,有C82种方案;对于另一个检查单位则只能从剩下的6人中抽出2人,有C62种方案,根据乘法原理,共有C(2,8)×C(2,6)=420种方案。故正确答案为C。解析2也是分为两步,先从8人中选出4人备选,则有有C(4,8)种方案,再从选拔出的4人中选取2人去第一个单位的方案有C(2,4)种方案,剩下的去第二个单位,无需挑选。根据乘法原理,70×6=420。故正确答案为C。速解两种方法本质没有区别,推荐使用第一种思路,直观。考查的是最基本的排列组合思想:”分类用加、分步用乘”,本题明显的按照步骤来筛选,所以中间乘法连接。 -
第12题:
问答题由3个节点构成的二叉树,共有多少种不同的形态?正确答案: 5解析: 暂无解析 -
第13题:
某人到食堂去买饭,主食有三种,副食有五种,他主食和副食各买一种,共有多少种不同的买法?
正确答案:15
-
第14题:
某条铁路线上,包括起点和终点在内原来共有7个车站,现在新增了3个车站,铁路上两站之间往返的车票不一样,那么,这样需要增加多少种不同的车票?( )
A.45
B.46
C.47
D.48
正确答案:D
以新站为起点,旧站为终点有3×7=21张;以旧站为起点,新站为终点有7×3=21张,以起点、终点均为新站有3×2=6张,以上共有21+2l+6=48张。 -
第15题:
某校开设9门课程供学生选修,其中A,B,C三门上课时间相同,学校规定,每位同学选修4门,共有多少种不同的选修方案?( )A.84
B.75
C.60
D.15答案:B解析:
-
第16题:
某班共有8名战士,现在从中挑出4人平均分成两个战斗小组分别参加射击和格斗考核,问共有多少种不同的方案A.210
B.420
C.630
D.840答案:B解析:
-
第17题:
如图所示,五个圆相连,现在用三种不同颜色分别给每个圆涂色,要求相连接的两个圆不能涂同种颜色,则共有多少种不同的涂色方法
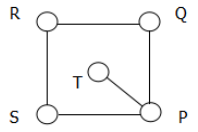 A.36
A.36
B.72
C.112
D.144答案:A解析:
-
第18题:
某单位共有10个进修的名额分到下属科室,每个科室至少一个名额,若有36种不同分配方案,问该单位最多有多少个科室?A. 7
B. 8
C. 9
D. 10答案:B解析:设共有n个科室,根据插板法,答案为。而,则n-1最大为7,n最大为8。答案为B选项。 -
第19题:
某班第一小组共有12位同学,现在要调换座位,使其中3个人都不坐自己原来的座位,其他9个人的座位不变,共有( )种不同的调换方法A.300
B.360
C.420
D.440
E.480答案:D解析:
-
第20题:
某市共有5个县,其位置如图所示,现用红、黄、绿、蓝4种颜色给地图上色,要求任意相邻的两个县的颜色不同,问共有多少种不同的上色方法?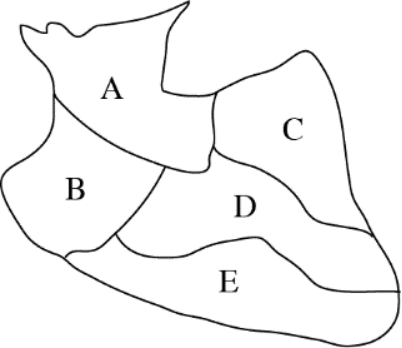 A.32
A.32
B.64
C.96
D.144答案:C解析:本题属于排列组合。

-
第21题:
由3个节点构成的二叉树,共有多少种不同的形态?
正确答案:5 -
第22题:
单选题从甲地到丙地有两种不同的方案,一种是从甲地经过乙地到丙地,另一种是从甲地直接到丙地。已知从甲地到乙地有3种走法,从乙地到丙地有2种走法,问从甲地到丙地一共有多少种不同的走法?()A6
B7
C10
D12
正确答案: C解析: 暂无解析 -
第23题:
多选题按份共有和共同共有的区别主要体现在( )。A成立的原因不同
B共有人应尽的义务不同
C对共有物的管理不同
D对第三人行使权利不同
E分割共有物的限制不同
正确答案: E,C解析:
