如下图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C 为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少？ (π取3.14)( )A. 13. 75cm2 B. 14. 25cm2 C. 14. 75cm2 D. 15. 25cm2

题目
如下图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C 为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少？ (π取3.14)( )


A. 13. 75cm2
B. 14. 25cm2
C. 14. 75cm2
D. 15. 25cm2
相似考题

1.下图中，每个小正方形网格都是边长为1的小正方形，则阴影部分面积最大是： AA BB CC DD

2.如下图所示，已知线段DE与AC平行，且与圆的半径相等，都为3厘米，0为圆的圆心。求图中阴影部分的面积。(π取3．14)

3. 某小区规划建设一条边长为10米的正方形绿地。如图所示，以绿地的2个顶点为圆心，边长为半径分别作扇形，把绿地划分为不同的区域。小区现准备在图中阴影部分种植杜鹃，则杜鹃种植面积为（ ）平方米。 A.100－25π B.200－35π C.200－50π D.100π－100

4.如下图所示，大正方形周长比小正方形周长多 80，阴影部分的面积为 880，大正方形 面积是： A.144 B.625 C.900 D.1 024

更多“如下图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C 为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少？ (π取3.14)( ) ”相关问题

  • 第1题：

    在4×7的方格板纸上面有如阴影所示的“9”字，每个小正方形的面积都是1平方厘米，阴影边缘是线段或圆弧，问纸板中阴影部分的面积是多少平方厘米？（ ）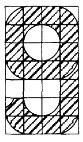


    A. 17
    B. 18
    C. 19
    D. 20

    答案：C
    解析：
    矩形纸板共有28个小正方形，图中非阴影部分比较少，其面积更容易计算。非阴影部分有三个完整的小正方形，经过平移其他部分可以拼成6个小正方形，因此非阴影部分的面积是9平方厘米，即阴影部分的面积是19平方厘米。

  • 第2题：

    如下图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C为圆心、 5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小多少？(π取3. 14)( )
    A. 13.75cm2 B. 14. 25cm2
    C. 14. 75cm2 D. 15. 25cm2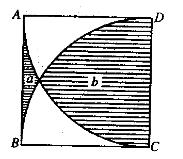


    答案：B
    解析：
    几何问题，利用容斥原理进行求解。分析题干可知，两个1/4圆覆盖的区城面积减去阴影部分b的面积再加上阴影部分a的面积等于正方形的面积，所以得到1/4X3.14X52X2-b+a=52，b-a = 14.25(cm2)。

  • 第3题：

    如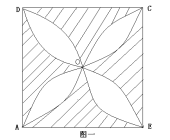，四边形ABCD是边长为1的正方形，弧AOB，BOC，COD，DOA均为半圆，则阴影部分的面积为



    答案：E
    解析：

  • 第4题：

    如下图所示，正方形被两条圆弧分割为四个部分，正方形的边长为10厘米，π=3.14，则面积A与B的差是多少平方厘米？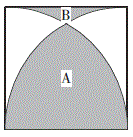

    A.60
    B.57C.54
    D.50

    答案：B
    解析：
    面积A等于1/4圆减去右侧空白，面积B等于正方形减去1/4圆和右侧空白，则所求为1/2圆减去正方形，即(1/2)×π×102-102=57平方厘米，选B。

  • 第5题：

    在边长为1的正方形ABCD中，AC与BD相交于O，以A、B、C、D分别为圆心，以对角线长的一半为半径画圆弧与正方形的边相交，如图，则图中阴影部分的面积为多少?(π=3．14)


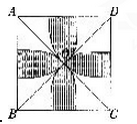    A.0．43
    B.0．57
    C.0．64
    D.0．71

    答案：C
    解析：

  • 第6题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )
    A. 11.75 B. 16.45 C. 19.625 D. 39. 25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10x10x2，所以大半圆的面积是1/2x1/4xπx10x10x2=25π（平方厘米）；
    小半圆的面积是π/2X5X5 = 12. 5π（平方厘米）；
    阴影的面积是25π-12. 5π=12. 5π=39. 25（平方厘米）。
    故本题选D。

  • 第7题：

    如图6-15所示,正方形ABCD的对角线∣AC∣=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,则阴影部分的面积为（ ）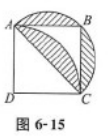

    A.π-1
    B.π-2
    C.π+1
    D.π+2
    E.π

    答案：B
    解析：

  • 第8题：

    如图，正方形ABCD的边长为10厘米，过它的4个顶点作一个大圆，过它的各边中点作一个小圆，再将对边中点用直线连接起来，那么图中阴影部分的面积为多少平方厘米？（π取3.14）( )

    A. 11.75 B. 16.45 C. 19.625 D. 39.25


    答案：D
    解析：
    根据圆的对称性，将圆沿直径上、下对折成右下图，这样阴影部分的面积就等于两个半圆之间的圆环。
    由正方形的面积等于正方形对角线平方的一半，可以求出正方形对角线的平方为10X10X2，所以大半圆的面积是1/2x1/4xπx10x10x2 = 25π(平方厘米)；
    小半圆的面积是1/2πx5x5 = 12. 5π(平方厘米)；
    阴影的面积是25π-12. 5π=12. 5π=39. 25(平方厘米)。
    故本題选D。

相关内容