在小学数学材料中，面积公式的推导过程包含的主要数学思想是()。 A.函数与方程思想，集合与对应思想 B.分类与整合思想，集合与对应思想 C.数学模型思想，公理化思想 D.有限与无限思想，化归与转化思想

题目
在小学数学材料中，面积公式的推导过程包含的主要数学思想是()。

A.函数与方程思想，集合与对应思想
B.分类与整合思想，集合与对应思想
C.数学模型思想，公理化思想
D.有限与无限思想，化归与转化思想
相似考题

1.简述中小学数学中接触的基本数学思想。

2.建构小学数学课堂教学策略的依据主要包括()。A、对学生学习数学成绩的要求B、对小学数学教育价值追求的基本认识C、对儿童学习数学过程的认识和理解D、对课堂学习过程的理解和诠释E、对教师自身价值的认识

3.对小学数学学科的再认识包含要形成“儿童数学观”、“现实数学观”以及()。A、科学数学观B、抽象数学观C、形式数学观D、生活数学观

4.促进学生发展的小学数学评价策略主要包含()A、过程性B、表现性C、发展性D、甄别性E、全面性

参考答案和解析
答案：D
解析：
在面积公式的推导中蕴含了转化、迁移的数学思想，如将平行四边形转化成长方形、将三角形转化成平行四边形、将梯形转化成三角形等；在圆面积公式的推导中蕴含了极限思想及化曲为直的思想，如把一个圆等分成若干个小扇形，当分成的小扇形越多，拼成的图形就越接近长方形，这其中蕴含着极限思想；而把一个圆转化成一个长方形来算它的面积，这又蕴含着转化思想和化曲为直的思想：故答案选D。
更多“在小学数学材料中，面积公式的推导过程包含的主要数学思想是()。 ”相关问题

  • 第1题：

    在小学数学教材中，应用列方程的方法求解应用题，渗透的主要数学思想是( )。

    A.分类与整合思想；或然与必然思想
    B.一般与特殊思想；符号化思想
    C.或然与必然思想；数学模型思想
    D.符号化思想；数学模型思想

    答案：D
    解析：

  • 第2题：

    下列关于数学思想的说法中，错误的一项是( )


    A.数学思想是现实世界的空间形式和数量关系反映到人的意识之中并经过思维活动产生的结果

    B.数学思想是要在现实世界中找到具有直观意义的现实原型

    C.数学思想是对数学事实与数学理论概念、定理、公式、法则、方法的本质认识

    D.数学思想是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观念

    答案：B
    解析：
    数学研究的对象是高度抽象概括的数量关系和空间形式，因此很难找到具有直观意义的数学原型，数学研究往往是基于理想情况的假设。

  • 第3题：

    数学模型思想不属于小学数学思想的范畴。


    正确答案:错误

  • 第4题：

    在小学阶段的数学思想主要有哪些？


    正确答案:符号思想、类比思想、分类思想、方程与函数思想、建模思想、极限思想。

  • 第5题：

    试举例分析小学数学运算规则学习中包含的主要内容。


    正确答案: 运算法则是关于运算方法和程序的规定，运算法则的理论依据称为算理。运算法则说的是怎样算，算理说的是为什么这样算。如：两位数笔算加法运算法则是“数位对齐、从个位加起、个位相加满十就向十位进一。”其中“数位对齐”、“个位相加满十向十位进一”的理论依据是“记数的位值原则。”这是算理。为什么要从个位加起呢，因为对于进位加法时，学生易出错，所以为减少错误，才提出“个位加起”。这是人为规定。

  • 第6题：

    现行的小学数学教材中渗透了集合、对应、函数、统计等数学思想，但没有极限思想。


    正确答案:错误

  • 第7题：

    克拉维斯在《星盘》中运用（）方法推导和角公式。

    • A、假设法
    • B、数学归纳法
    • C、面积变换法
    • D、体积法

    正确答案:C

  • 第8题：

    单选题
    公元3世纪末，数学家（）在《数学汇编》中推导了和角公式。
    A

    洛必达

    B

    约翰·伯努利

    C

    斯蒂尔

    D

    帕斯卡


    正确答案： A
    解析： 暂无解析

  • 第9题：

    单选题
    以下论述属于小学数学教学过程特征的是（）
    A

    小学数学教学的过程是形象思维与逻辑思维、合情推理与论证推理相结合的过程

    B

    小学数学教学的过程是逻辑思维与论证推理为主的过程

    C

    小学数学教学的过程是形象思维与合情推理为主的过程

    D

    小学数学教学的过程是逻辑思维与合情推理为主的过程


    正确答案： A
    解析： 暂无解析

  • 第10题：

    判断题
    数学模型思想不属于小学数学思想的范畴。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第11题：

    问答题
    教学设计题：试分析平行四边形面积公式推导过程中体现的数学思想。

    正确答案： 平行四边形面积公式推导采用的割补拼接法，通过将平行四边形进行分割拼接成长方形然后计算其面积的方法体现了数学中的转化思想。转化思想是由一种形式变换成另一种形式的思想方法，而其本身的大小是不变的。
    解析： 暂无解析

  • 第12题：

    单选题
    克拉维斯在《星盘》中运用（）方法推导和角公式。
    A

    假设法

    B

    数学归纳法

    C

    面积变换法

    D

    体积法


    正确答案： A
    解析： 暂无解析

  • 第13题：

    小学数学《梯形的面积》
    一、考题回顾
    题目来源5月19日 上午 山东省济宁市 面试考题
    试讲题目1.题目：梯形的面积
    2.内容：



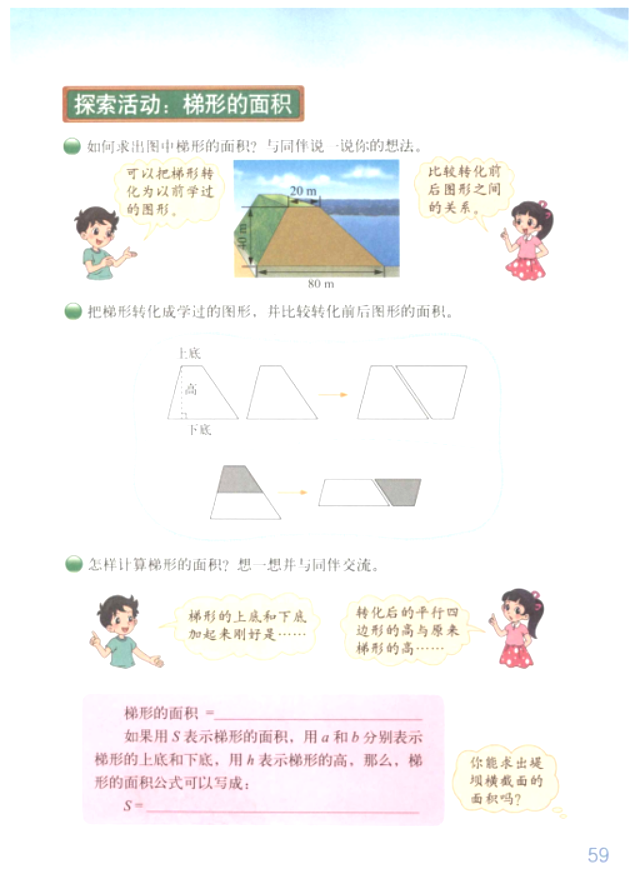
    3.基本要求：
    (1)引导学生自主推导出梯形的面积公式;
    (2)教学过程中有互动环节;
    (3)试讲时间10分钟左右。
    (4)要有合适的板书。
    答辩题目1.你在教学过程中，当有学生在梯形面积的推导过程中有不同的思路时，你是怎么处理的?
    2.本节课中用到什么数学思想方法?


    答案：
    解析：
    二、考题解析
    【教学过程】
    (一)引入新课
    复习平行四边形的面积公式及推导过程。提问：我们已学会了用转化的方法推导平行四边形面积的计算公式，那怎样计算梯形的面积呢?
    引出课题。
    (二)讲解新知
    提问：你能仿照求平行四边形面积的办法，把梯形也转化成已学过的图形，计算出它的面积吗?
    学生操作，教师巡回观察指导。



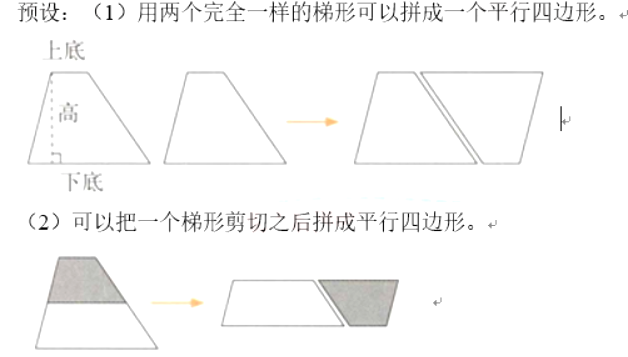
    提问：转化得到的平行四边形的底和高与梯形的底和高有什么关系?每个梯形的面积与拼成的平行四边形的面积有什么关系?
    学生汇报讨论结果。
    并尝试总结梯形面积的计算公式：梯形的面积=(上底+下底)×高÷2)，字母表示公式为S=(a+b)h÷2。
    (三)课堂练习
    练习：求出堤坝横截面的面积。



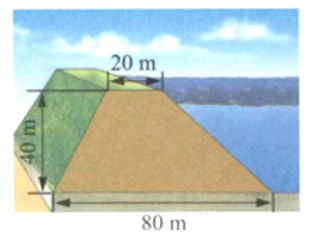
    (四)小结作业
    提问：今天有什么收获?引导学生回顾：梯形面积公式的推导过程。
    作业：课后练习。



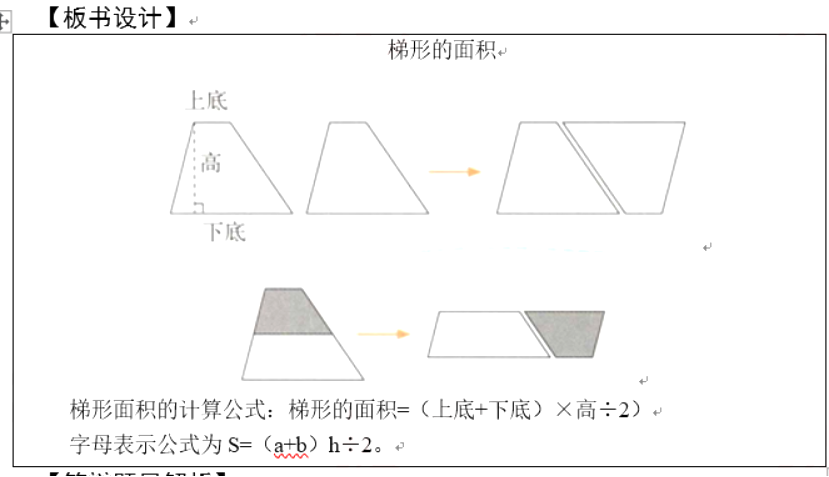
    梯形的面积
    梯形面积的计算公式：梯形的面积=(上底+下底)×高÷2)
    字母表示公式为S=(a+b)h÷2。
    【答辩题目解析】
    1.你在教学过程中，当有学生在梯形面积的推导过程中有不同的思路时，你是怎么处理的?
    【参考答案】
    作为老师，首先应该鼓励学生的创新性思维，鼓励他们多动手操作、动脑思考;然后与其他学生一起验证这种方法的正确与否，得到什么结论;最后，鼓励学生还有没有其他的推导方法，能不能通过其他方式，转化推导出梯形的面积。
    2.本节课中用到什么数学思想方法?
    【参考答案】
    转化的思想方法。把梯形的面积转化为平行四边形的面积，从而推导出梯形的面积公式。

  • 第14题：

    明朝是我国古代数学发展的衰落期，但对小学数学教育来说，（）的普及和（）的引入，彻底打破了筹算作为主要运算手段在我国古代数学学习中长达2000多年的“统治”地位，成为小学数学教学的主要内容。


    正确答案:珠算算法；笔算

  • 第15题：

    在小学数学教学中圆面积公式的推导使用了（）

    • A、解方程思想
    • B、出入相补原理
    • C、极限思想
    • D、代数思想

    正确答案:C

  • 第16题：

    对小学数学学科性质的再认识包含着（）、（）、（）等这样三个数学观。


    正确答案:儿童数学观；生活数学观；现实数学观

  • 第17题：

    以下论述属于小学数学教学过程特征的是（）

    • A、小学数学教学的过程是形象思维与逻辑思维、合情推理与论证推理相结合的过程
    • B、小学数学教学的过程是逻辑思维与论证推理为主的过程
    • C、小学数学教学的过程是形象思维与合情推理为主的过程
    • D、小学数学教学的过程是逻辑思维与合情推理为主的过程

    正确答案:A

  • 第18题：

    《周易》中所包含的数学思想有：（1）组合数学的萌芽（2）（）（3）坐标系思想。


    正确答案:二进制

  • 第19题：

    公元3世纪末，数学家（）在《数学汇编》中推导了和角公式。

    • A、洛必达
    • B、约翰·伯努利
    • C、斯蒂尔
    • D、帕斯卡

    正确答案:D

  • 第20题：

    问答题
    在小学阶段的数学思想主要有哪些？

    正确答案： 符号思想、类比思想、分类思想、方程与函数思想、建模思想、极限思想。
    解析： 暂无解析

  • 第21题：

    填空题
    《周易》中所包含的数学思想有：（1）组合数学的萌芽（2）（）（3）坐标系思想。

    正确答案： 二进制
    解析： 暂无解析

  • 第22题：

    问答题
    简述中小学数学中接触的基本数学思想。

    正确答案： 在数学思想中，有一类思想是体现或应该体现于基础数学中的具有奠基性和核心性的思维成果，这些思想可以称之为基本数学思想。
    1.分类思想
    按某种标准，将研究的数学对象分成若干部分进行分析研究，从而把对象简单化。如整数的分类，角的分类
    2.数形结合思想
    将一个代数问题用图形来表示，或把一个几何问题记为代数的形式，通过数与形的结合，可使问题转化为易于解决的情形。如，初中教学中的数轴内容
    3.方程和函数思想
    方程思想就是在已知数与未知数之间建立一个等式，把生活语言”翻译“成代数语言。函数思想是指要用运动变化的观点分析、研究具体问题中的数量关系，用函数的关系表示出来并加以研究，以求得问题的解决
    4.集合思想
    所谓集合，指具有某种特定性质的事物的全体。任何事物，或者属于这一集合，或者不属于这一集合，二者必居其一且仅居其一。
    5.化归思想
    所谓化归即转化、归结的意思。化归思想是根据问题解决的需要转变研究对象的内容或形式，即把困难的问题转化为已知的或新形式的问题，利用变换后新形式的方便和变换中的不变性，通过对已知问题或新形式问题的解决，获得原问题的解决。所以化归思想也称变换思想。除此之外，中小学数学中接触的基本数学思想还有一般化思想、极限思想、公理化与结构思想、整体思想、建模思想等等。
    解析： 暂无解析

  • 第23题：

    单选题
    在小学数学教学中圆面积公式的推导使用了（）
    A

    解方程思想

    B

    出入相补原理

    C

    极限思想

    D

    代数思想


    正确答案： C
    解析： 暂无解析

相关内容