如右图，在梯形ABCD中，点E、F分别是腰AB、CD上的点． (1)证明：如果E、F为中点时，有 EF=1/2(AD+BC)； (2)请写出(1)中命题的逆命题，并判断该逆命题是否成立，若成立，请给予证明；若不成立，请说明理由．
题目
如右图，在梯形ABCD中，点E、F分别是腰AB、CD上的点．
(1)证明：如果E、F为中点时，有 EF=1/2(AD+BC)；
(2)请写出(1)中命题的逆命题，并判断该逆命题是否成立，若成立，请给予证明；若不成立，请说明理由．
(1)证明：如果E、F为中点时，有 EF=1/2(AD+BC)；
(2)请写出(1)中命题的逆命题，并判断该逆命题是否成立，若成立，请给予证明；若不成立，请说明理由．
相似考题
更多“如右图，在梯形ABCD中，点E、F分别是腰AB、CD上的点． ”相关问题
-
第1题：
如图。在直角梯形ABCD中，AB∥CD，∠BAD=90o，且AB=8，AD=3，CD=4，动点P，Q分别以点B和点A为起点同时出发，点P沿B→A，以每秒1个单位速度运动，终点为点A；点Q沿A→D→C→B，以每秒1.5个单位速度运动，终点为点B。设△APQ的面积为y，运动时间为x。
(1)求y关于x的函数解析式y=f(x)；
(2)画出函数y=f(x)的图象。
答案：解析：
(2)函数图象如图所示：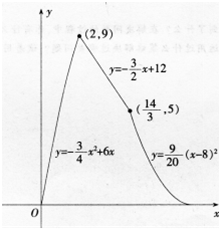
-
第2题：
在平行四边形ABCD中，∠DAB=60，AB=15cm，已知圆O的半径等于3cm，AB，AD分别与圆O相切于点E，F.圆0在平行四边形ABCD内沿AB方向滚动，与BC边相切时运动停止．试求圆O滚过的路程．答案：解析：
-
第3题：
如右图，在直角梯形ABCD中，AB,∥CD，AD⊥CD，AB=1cm，AD=6cm，CD=9cm，则BC=________cm．
答案：解析：
-
第4题：
如右图，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为（ ）．
A.20
B.18
C.16
D.15答案：C解析：由“菱形的每一条对角线平分-组对角”知，在△ABC中，∠BAC=60。，又由“菱形的四条边相等”知，△ABC为正三角形，得AB=4.故菱形的周长为16. -
第5题：
平行四边形ABCD如右图所示，E为AB上的一点，F、G分别是AC和DE、DB的交点。若AB=3AE，则四边形BEFG与ABCD的面积之比是：A.2︰7
B.3︰13
C.4︰19
D.5︰24答案：D解析：第一步，本题考查几何问题，属于平面几何类，用赋值法解题。
第二步，题干没给出具体数值，可以采用赋值法解题。赋值AB=3，平行四边形ABCD的高为4，则AE=1；由于△AEF相似于△CDF，则两个三角形的高之比为AE：DC=1︰3，可知△AEF的高为
4*1/4=1。△ABG与△CDG全等，则△ABG的高为4÷2=2。
第三步，四边形BEFG面积=△ABG面积-△AEF面积=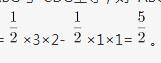
四边形ABCD面积=3×4=12，两者之比为 ︰12=5︰24。
因此，选择D选项。 -
第6题：
下图中ABCD为边长10米的正方形路线，E为AD中点，F为与B相距3米的BC上一点，从E点到F点有小路EGHF，小路的每一段都与AB垂直或平行，且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒，则其以相同速度经EGHF从E点匀速运动到F点用时多少秒？
A.12
B.10
C.9
D.8答案：D解析：第一步，本题考查行程问题，属于基本行程类。
第二步，E为AD中点，则EA＝10÷2＝5（米），甲经过EABF从E点到F点所走路程为AE＋AB＋BF＝5＋10＋3＝18（米）；标记HF的转弯点为M、N，那么甲经EGHF从E点到F点所走路程为EG＋GH＋HM＋MN＋NF＝（EG＋HM＋NF）＋GH＋MN＝10＋2＋（5＋2－3）＝16（米）。
第三步，两种路线速度相同，路程比为18∶16＝9∶8，那么所用时间之比为9∶8，第一种路线用时9秒，那么第二种路线用时8秒。
因此，选择D选项。 -
第7题：
如图，在梯形ABCD中，AB//CD，O为AC与BD的交点，CO=2AO，则梯形ABCD与三角形AOB的面积之比为：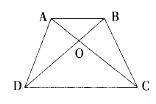
A.6：1
B.7：1
C.8：1
D.9：1答案：D解析：在梯形中，上底与下底平行，可得△AOB~△COD，其面积之比等于对应边AO、CO之比的平方，为1:4。△AOB与△BOC可看成两个等高的三角形，面积之比等于底AO、CO之比，为1:2。显然△AOD与△BOC面积相等。设△AOB面积为1，则梯形面积为1+2+2+4=9。故所求为9:1。 -
第8题：
某构件受力简图如右图，则荷载P 对于点O 的力矩Mo 为（ ）。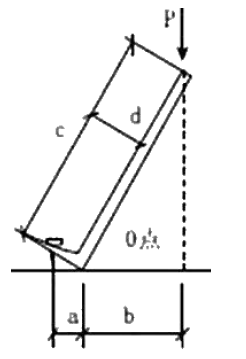
A.P·a
B.P·b
C.P·c
D.P·d答案：B解析：本题考查的是平面力系的平衡条件及其应用。力矩=力的大小×力的作用方向到支点的距离=P×b。 -
第9题：
某位教师在讲完《相交线与平行线》这部分内容后，设计了一节《相交线与平行线》的复习课．在这节课中，他设计了如下一组题：
题1．如图3．BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90。。
①BE与DE有什么样的位置关系 请说明理由。
②AB与CD有什么样的位置关系 请说明理由。
题2．如图4，AB∥CD且∠1+∠2=800：，求∠BED的度数。
题3．如图5，AB∥CD直线1交AB于点F、交CD于点G，点E是线段GF上的一点(点E
与点F、G不重合)，设∠ABC＝β,∠BED=γ。试探索a，β、γ之间的关系，并说明理由。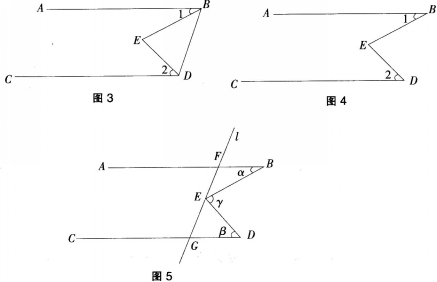
阅读上述教学设计片段，完成下列任务：
(1)从这组习题分析这节复习课的教学目标；(8分)
(2)分析这三道题的设计意图，并说明这组习题设计的特点；(10分)
(3)请你在图5的基础上，编一道类似习题，并给出答案。(12分)答案：解析：(1)知识与技能目标：能够利用平行线的性质与判定定理，判断两条直线是否平行；能够利用两直线相交的性质求相交直线的交角度数。
过程与方法目标：学生通过对两直线的位置关系进行观察、猜想、探索等过程，初步形成几何直观，发展形象思维与抽象思维．锻炼合情推理和演绎推理能力，并能清晰地表达自己的想法。
情感态度与价值观目标：在学习过程中，体验获得成功的乐趣，锻炼克服困难的意志，建立自信心。养成认真勤奋、独立思考、合作交流、反思质疑等学习习惯，形成实事求是的科学态度。
(2)第一道题目，给出已知条件BE平分厶4BD，DE平分L_BDC且∠1+∠2=90。，通过两个问题引导学生思考，利用角平分线的性质，先判断出BE与DE的位置关系，进而利用两直线平行的判定定理判断AB与CD的位置。这道题目结合学生的已有知识经验，加深巩固对两直线平行判定定理的应用。为第三道题目的猜想做铺垫。
第二道题目．在第一道题目的基础之上对题目进行变形，已知AB∥CD且∠l+∠2=80。，结合对一道题目解题的经验，利用两直线平行的性质求出∠BED的度数。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，并为第三道题目的猜想做铺垫。
第三道题目。在前两道题目的铺垫下，将具体角变为抽象角，学生结合前两道题目的解题经验，进行猜想、探索证明。这道题目的主要设计意图为加深巩固学生对两直线平行的性质的应用，提高学生合情推理和演绎推理能力，将所学知识融会贯通。
三道题目逻辑联系紧密，考虑到学生的认知顺序，遵循由浅入深，由易到难，由表及里等一系列规律，让学生能够拾级而上，循序渐进，步步深入。以达到能够将所学知识灵活运用并初步形成几何直观，发展形象思维与抽象思维，锻炼合情推理和演绎推理能力的目的。
(3)如图5，直线l交AB于点F、交CD于点G，点E是线段GF上的一点(点E与点F、G不重合)，设∠ABE=01，∠CDE=fl，LBED=y。试探索γβα满足何条件的时候，AB与CD平行，并说明理由。
当a+B＝Y时，AB与CD平行。连接BD，因为三角形BDE的内角和为180度，所以∠EBD+∠EDB=1800一∠BDE，若β+α=γ，则∠EBD+∠EDB+α+β=1800～∠BED+α+β=1800，则AB与CD平行。 -
第10题：
图4-22中，均质杆AB重力为F,用铅垂绳CD吊在天花板上，A、B两端分别靠在光滑的铅垂墙面上，则A、B两端约束力的大小是( )。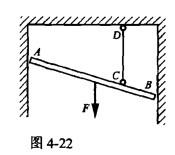
A. A、B两点约束力相等 B. B点约束力大于A点约束力
C. A点约束力大于B点约束力 D.无法判断答案：A解析：提示：A、B处为光滑约束，其约束力均为水平并组成一力偶，与力F和CD杆约束力组成的力偶平衡。 -
第11题：
如图，在一张矩形纸片ABCD中，AB=4，BC=8。点E，F分别在AD，BC上，将纸片ABCD沿直线EF折叠，点C落在AD上的一点日处，点D落在G处，有以下四个结论：①四边形CFHE是菱形；②EC平分∠DCH；③线段BF的取值范围为3≤BF≤4；④当点H与点A重合时, 。以上结论中，你认为正确的有( )个。
A.1
B.2
C.3
D.4答案：C解析：
-
第12题：
单选题已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）A40°
B50°
C60°
D70°
正确答案： B解析： 暂无解析 -
第13题：
如下图，平行四边形ABCD的对角线相交于点O，直线EF经过点O，分别与AB，CD的延长线交于点E，F．求证：四边形AECF是平行四边形．
答案：解析：证明：如右图所示，∵四边形ABCD为平行四边形，∴BO=DO，
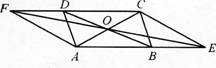
又∵AB∥CD，∴∠FDO=∠EB0
-
第14题：
如图,D是△ABC内的一点，BD⊥CD，AD=6，BD=8，CD=6，E，F，G，H分别是AB，AC，CD， BD的中点．则四边形EFGH的周长是()。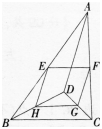
A.12
B.14
C.15
D.16答案：D解析：因为BD⊥CD，BD=8，CD=6，由勾股定理可知BC=10。由三角形中位线定理可知EH=FG=
-
第15题：
如右图，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙0上，且∠OBA=40°，则∠ADC=_______．
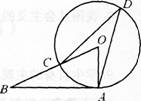答案：解析：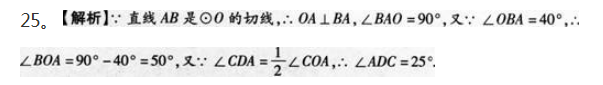
-
第16题：
如右图所示，梯形ABCD的对角线AC⊥BD,其中AD＝1/2,BC＝3,AC＝14/5 ,BD＝2.1.问梯形ABCD的高AE的值是：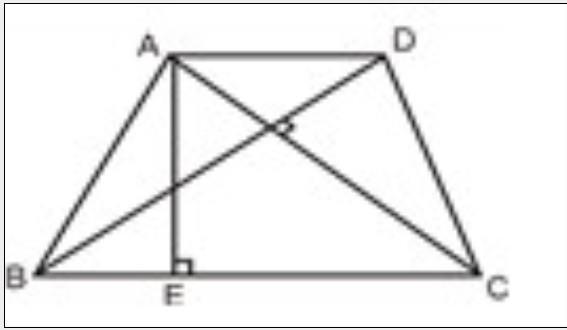
A. 43/24
B. 1.72
C. 42/25
D. 1.81答案：C解析：解题指导： C。 -
第17题：
如图所示，梯形ABCD的两条对角线AD、BC相交于O，EF平行于两条边且过O点。现已知AB=6，CD=18。问EF的长度为多少？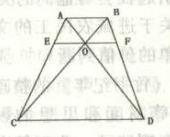
A. 8.5
B. 9
C. 9.5
D. 10答案：B解析：解题指导： 18*BF/BD=6*DF/BD， BF/DF＝1：3， OF/CD=1:4， OE/CD=1:4， EF=CD/2＝9，故答案为B。 -
第18题：
如图，ABCD为矩形，AB=4，BC=3，边CD在直线L上，将矩形ABCD沿直线L作无滑动翻转，当点A第一次翻转到点A1位置时，点A经过的路线长为：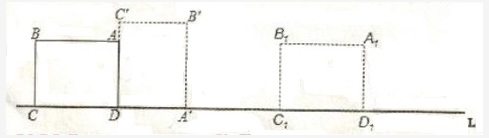
A7π
B6π
C3π
D3π/2答案：B解析：
-
第19题：
如右图，两只小爬虫甲和乙从A点出发，沿长方形ABCD的边，按箭头方向爬行，在离C点32厘米的E点它们第一次相遇；在离D点16厘米的F点第二次相遇；在离A点16厘米的G点第三次相遇。求长方形的边AD长多少厘米？ AB边长多少厘米？（ ）
A. 24 36 B. 48 54
C. 36 48 D. 48 64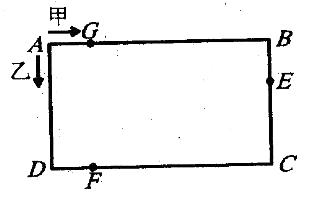
答案：D解析：设AD=BC=x厘米，AB = CD =y厘米，则乙虫第一次相遇时走了(x + y + 32)厘米，第一次相遇后到第二次相遇时又走了[(x - 32)+y +x+16]厘米。由于每次相遇时，两虫合起来走了一周，因此，两虫每次相遇时走的路程均相等。列方程得x+y+32= (x-32) +y+x+ 16，x= 48。
同理，甲虫第一次相遇时走了(y+x-32)厘米，第二次相遇到第三次相遇时走了(16 +x+16)厘米， 列方程得y+x-32 =16+x+16，y=64。
故长方形的边AB长64厘米，AD长48厘米，所以本题正确答案为D。 -
第20题：
如右图所示，梯形ABCD的对角线AC丄BD，其中AD=1/2，BC=3，AC=2，BD=2.1，则梯形ABCD的髙AE的值是()。
答案：C解析：由ACXBD=(AD+BC)XAE=>AE=42/45。 -
第21题：
如图6，AB是⊙E的直径，C是直线AB上一点，CD切⊙E于点D，且∠A=25o，则∠C= ______度。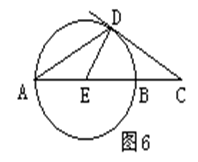
答案：解析：40 -
第22题：
某构件受力简图如右图，则点O 的力矩Mo 为（ ）。（2015 年真题）
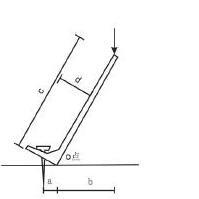A．P·a
B．P·b
C．P·c
D．P·d答案：B解析：本题考查的是力矩的计算方法。力矩=力×力臂。力臂是力矩中心点O 至力P 的作用线的垂直距离，本题中即把P 的作用线向下延长，再取O 点至该延长线的垂直距离，最后承上力P，故选B。 -
第23题：
已知圆内接四边形ABCD中，AB、CD的延长线交与点F，则F=（）
- A、40°
- B、50°
- C、60°
- D、70°
正确答案:A