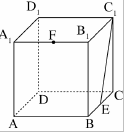
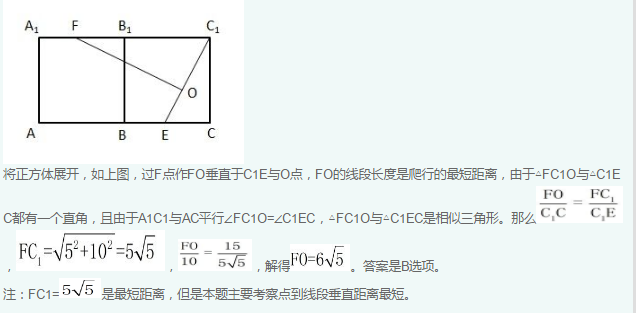
如右图所示,一个边长为10厘米的正方体木块ABCD-A1B1C1D1,点E、F分别是BC、A1B1的中点,C1E是用蜂蜜画的一条线段,一只蚂蚁在点F处,要想沿正方体表面最快到达蜂蜜所在线段C1E,它所爬行的最短距离是多少厘米?
题目
如右图所示,一个边长为10厘米的正方体木块ABCD-A1B1C1D1,点E、F分别是BC、A1B1的中点,C1E是用蜂蜜画的一条线段,一只蚂蚁在点F处,要想沿正方体表面最快到达蜂蜜所在线段C1E,它所爬行的最短距离是多少厘米?
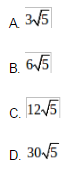

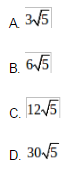
相似考题
参考答案和解析
答案:B
解析:
知识点:体积计算

更多“如右图所示,一个边长为10厘米的正方体木块ABCD-A1B1C1D1,点E、F分别是BC、A1B1的中点,C1E是用蜂蜜画的一条线段,一只蚂蚁在点F处,要想沿正方体表面最快到达蜂蜜所在线段C1E,它所爬行的最短距离是多少厘米? ”相关问题
-
第1题:
一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点,设正方体边长为a,问该蚂蚁爬过的最短路程为:
 答案:B解析:
答案:B解析: -
第2题:
如右图所示,一个正方体木块六个面上分别写着数字,相对面上两个数字的和为20。现在正方体木块的上面是9,正面是13,右面是5。如果先将木块从左向右翻转2018次,再由前向后翻转2019次,这时木块正面数字是:
 A.9
A.9
B.11
C.13
D.15答案:B解析:第一步,本题考查循环周期问题和几何问题。
第二步,由正方体六个面上相对面的两个数字之和为20,得三组相对面的数值分别为(9、11)(13、7)(5、15)。先将木块从左向右翻转2018次,如此翻转,无论翻转多少次,正面数字不发生变化,但2018÷4=504……2,即向上面为11;再由前向后翻转2019次,4个面一个循环周期,2019÷4=504……3,余数为3,由前向后翻,此时正面数字正好是原来向上的面11。 -
第3题:
数学运算。在这部分试题中.每道试题呈现一段表述数字关系的文字,要求你迅速、准确地计算出答案。
一只蚂蚁从图的正方体A顶点沿正方体的表面爬到正方体C顶点。设正方体边长为a,问该蚂蚁爬过的最短路程为()。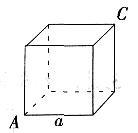
A.
B.
C.
D.答案:B解析:根据两点之间线段最短,将正方体展开为平面。根据勾股定理A到C的直线距离为。
-
第4题:
先将线段AB分成20等分,线段上的等分点用"A"标注,再将该线段分成21等分,等分点 用“O”标注(AB两点都不标注),现在发现"A"和“O”之间的最短处为2厘米,问线段AB 的长度为多少?( )
A. 2460厘米 B. 1050厘米
C. 840厘米 D. 680厘米答案:C解析:不妨设线段AB长度为x,且从左端开始计算距离。先将线段AB分成20等分,线段上的等分点用“A’’标注,则每个“A"的位置为nx/20, 且 l n 19;再将该线段分成21等分,等分点用“O"标注,则每个“O"的位置为kx/21, 且 l k 20;nx/20— kx/21 = x(21n—20k)/420,则显然当 n = k=l 时候,此式值最小。 因为“A’’和“O”之间的最短处为2厘米,即x/420 = 2,解得x=840厘米。 -
第5题:
如图,圆锥高 厘米,底面半径为6厘米,一只蚂蚁从A.点沿圆锥侧面爬行到B.点,则最短的距离为_________厘米。
厘米,底面半径为6厘米,一只蚂蚁从A.点沿圆锥侧面爬行到B.点,则最短的距离为_________厘米。

 A.12
A.12
B.
C.6π
D.24答案:B解析:

-
第6题:
如图6-28所示,有一圆柱,高h=3厘米,底面半径r=3厘米,在圆柱下底面的点A处有一只蚂蚁,沿圆柱表面爬行到同一纵切面的斜上方的B点,则蚂蚁沿表面爬行时最短路程是( ).(π≈3)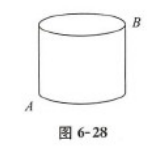
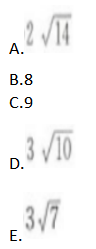 答案:C解析:
答案:C解析:
-
第7题:
一只小虫从棱长为2的正三棱锥(如图)中的A点爬到B点(为所在线段的中点),且小虫 只在面OAC和面OCD中移动。问该小虫爬过的最短路程为( )。
 答案:B解析:
答案:B解析: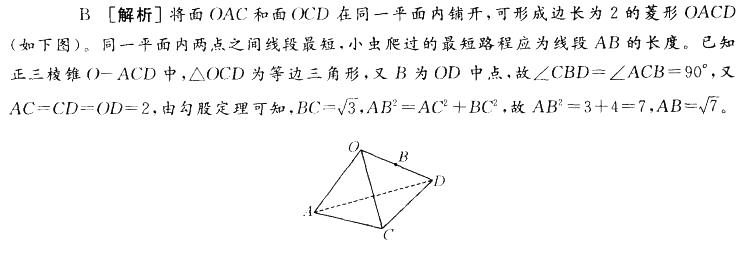
-
第8题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100㎝2
B400㎝2
C500㎝2
D600㎝2
正确答案: B解析:
在一个边长为20㎝的大正方体中挖去1个边长为10㎝的小正方体,则大正方体原有的6个面只有其中1个面的面积减少了100㎝2,而小正方体则多出了5个100㎝2的面,因此大正方体的面积增加了400㎝2。 -
第9题:
小庄要制作一个工业模具。他在一个边长4厘米的正方体上表面正中心位置向下挖掉一个直径2厘米、高2厘米的圆柱体,接着再向下挖掉一个直径1厘米、高1厘米的小圆柱体(如右图所示)。那么,该模具的表面积约为多少平方厘米?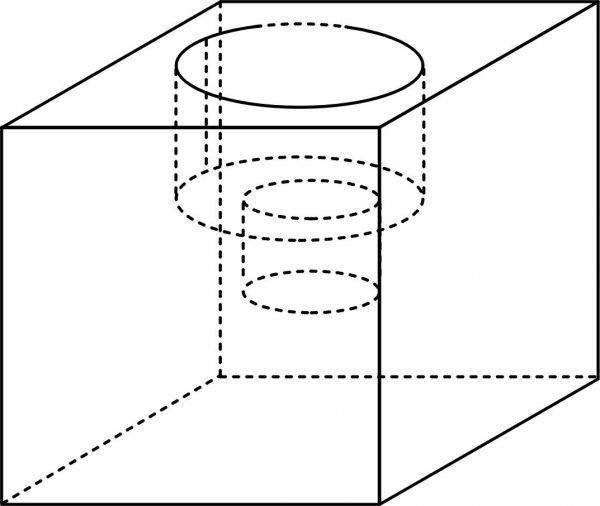 A.82.8
A.82.8
B.108.6
C.111.7
D.114.8答案:C解析:第一步,判断本题为几何问题,采用公式法。第二步,该模具表面积可分为三个部分:①将所有圆柱体的底面补到正方体上表面,补成一个正方体的表面积,为4×4×6=96(平方厘米);②一个大圆柱体的侧表面积,为2π×1×2=4π(平方厘米);③一个小圆柱体的侧表面积,为2π×0.5×1=π(平方厘米)。第三步,可知整个模具的表面积是96+4π+π≈111.7(平方厘米)(取π=3.14)。因此,选择C选项。 -
第10题:
一个正方体的边长为1,一只蚂蚁从其一个角出发,沿着正方体的棱形进,直到经过该正方体的每一条棱为止(经过一个顶点即算作经过该顶点所连接的3条棱)。则其最短的行进距离为( )。A. 3
B. 4
C. 5
D. 6答案:C解析:蚂蚁行进路径如下图2所示,故本题答案为C选项。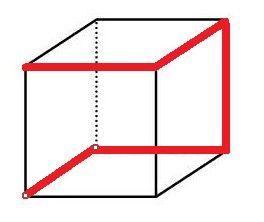
-
第11题:
一只蚂蚁位于2×2×2正方体空心框架的A点,向B点爬行。如果只准沿着框架线条爬,则最短路线一共有几条?
{图}A.64
B.90
C.99
D.100答案:C解析:要求最短路径,则蚂蚁在每个点只能向上、前、右爬。记向右爬为x,向前爬为),,向上爬为z,则路径相当于对xxyyzz进行排列,有c:xC:=90,选8。 -
第12题:
一个边长为a的正方体木块漂浮在水池中,木块底部距离水面10厘米,如果将一个边长为2a的相同材质的正方体木块也放入该水池,则这一木块底部应距离水面( )。A.5厘米
B.10厘米
C.20厘米
D.40厘米答案:C解析:浮力考查。原本边长为a的立方体漂浮水中,由漂浮原理可知,物体密度小于液体密度,并且此时的重力G?=浮力F?,即ρ物ga3=ρ水g a2·h?。后将相同材质边长为2a的立方体放置水中,由前面可知物体密度小于水可知依然漂浮,此时重力G?=浮力F?,即ρ物g(2a)3=ρ水g(2a)2·h?,又因为G?=8G?,所以F?=8F?,因此可得h?=2h?,因此这块木块底部距离水面500px。 -
第13题:
一只蚂蚁从右图的正方体的A顶点沿正方体的表面爬到正方体的C顶点,设正方体边长为a,问该蚂蚁爬过的最短路程为: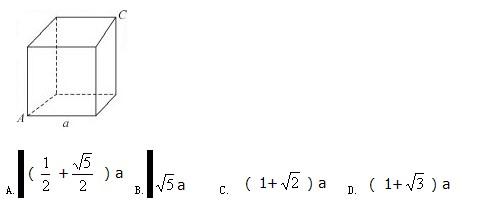
A.A B. B C. C D. D答案:B解析:解题指导: 该最短路程为√[1+﹙22a﹚]=√5a。故答案为B。 -
第14题:
一只蚂蚁位于2×2×2正方体空心框架的A点,向B点爬行。如果只准沿着框架线条爬。则最短路线一共有几条?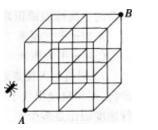 A.64
A.64
B.90
C.99
D.100答案:B解析:要求最短路径,则蚂蚁在每个点只能向上、前、右爬。记向右爬为x,向前爬为y,向上爬为
-
第15题:
如图,正方体ABCD-A1B1C1D1中,E,F,G分别为AA1,A1D1,BC的中点,则异面直线EF与D1G所成角的大小为__________。
 答案:解析:连接AD1,AG,由于EF平行于AD1,则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2,在△AD1G中,D1G=3,根据余弦定理,cos∠AD1G=
答案:解析:连接AD1,AG,由于EF平行于AD1,则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2,在△AD1G中,D1G=3,根据余弦定理,cos∠AD1G=

-
第16题:
单选题若在一个边长为20厘米的正方体表面上挖一个边长为10厘米的正方体洞,问大正方体的表面积增加了多少?( )A100cm2
B400cm2
C500cm2
D600cm2
正确答案: C解析:
在一个边长为20cm的大正方体中挖去一个边长为10cm的小正方体,则大正方体原有的6个面只有其中一个面的面积减少了100cm2,而小正方体则多出了5个100cm2的面,因此大正方体的面积增加了400cm2。