已知圆的直径AB两端点的坐标A（1，-1)，B（-1，1)，求圆的标准方程。

题目

已知圆的直径AB两端点的坐标A（1，-1)，B（-1，1)，求圆的标准方程。

相似考题

1.20 （本小题满分13分）已知椭圆C的中心在原点，焦点在x 轴上，以两个焦点和短轴的两个端点为顶点的圆边形是一个面积为8的正方形（记为Q）（1） 求椭圆C的方程：

2.如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。 (1)求证：BE是⊙0的切线； (2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。

3.如图：已知圆0，点P在圆外，D，E在圆上，PE交圆于C，PD与圆相切，G为CE上一点且满足PG=PD,连接DG并延长交圆于A，作弦AB⊥EP，垂足为F。 (1)求证：AB为圆的直径； (2)若AC=BD，AB=5，求弦DE的长。

4.已知一正常标准直齿圆柱齿轮，齿数Z1=36，齿顶圆直径dal=105mm，配制与其啮合的齿轮，要求中心距a=116.25mm，试求这对齿轮的分度圆d1、d2直径和齿数z2。注：Dal=m(Z1 +2)

参考答案和解析
和
更多“已知圆的直径AB两端点的坐标A（1，-1)，B（-1，1)，求圆的标准方程。”相关问题

  • 第1题：

    已知圆过A(1，3)，B(5，1)两点，且圆心在y轴上，则圆的标准方程为__________。


    答案：
    解析：

  • 第2题：

    在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。
    (1)求。的值及直线Z的直角坐标方程；
    (2)圆C的参数方程为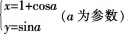试判断直线Z与圆C的位置关系。


    答案：
    解析：
    所以直线l与圆C相交。

  • 第3题：

    一对标准直齿圆柱齿轮传动，已知两齿轮齿数分别为40和80，并且测得小齿轮的齿顶圆直径为420mm，求两齿轮的分度圆d1、d2，中心距a，齿距p，齿厚s，以及大齿轮的齿顶圆da2和齿根圆df2。

    略

  • 第4题：

    一标准直齿圆柱齿轮副，已知：齿数z1=26，z2=65，测得中心距a=366mm。求齿轮的模数m、大齿轮的分度圆直径d2、齿距p、齿顶圆直径da和齿高h。


    正确答案: a=m（z1 +z2）/2所以m=8.04 mm查表取标准值m=8mm
    分度圆d2 = mz2=520mm        齿距P =πm=25.12mm
    齿顶圆da2  =m（z2+2）=4288mm   齿顶高ha=m=8mm

  • 第5题：

    计算题：已知相啮合的一对标准直齿圆柱齿轮，Z1=20，Z2=50，传动中心距a=210。求两齿轮的分度圆直径d1和d2？


    正确答案: 齿轮中心距等于两个齿轮分度圆的半径之和：（d1+d2）/2＝210
    两齿轮的分度圆之比等于两齿轮的齿数比，即：d2/d1＝Z2/Z1＝2.5，得d2＝2.5d1，代入上式
    得：（d1+2.5d1）/2＝210
    3.5d1＝420，得d1＝120，所以d2＝2.5d1＝300

  • 第6题：

    计算题：有一对标准直齿圆柱齿轮，Z1=25，Z2=70，m=3mm，试求小齿轮的分度圆直径d1，齿顶圆直径da1，齿根圆直径df1。


    正确答案: d1=mZ1=3×25=75mm
    da1=m（Z1+2）=3×（25+2）=81mm
    df1=m（Z1-2）=3×（25-2.5）=67.5mm

  • 第7题：

    已知相啮合的一对标准直齿圆柱齿轮，其齿顶圆直径da=224mm，齿数z=30。求模数m，齿厚s，分度圆直径d，齿根圆直径df，全齿高h。


    正确答案: 因da=m（Z+2）=224，有m=7
    则：s=πm/2=10.99mm
    d=mZ=7×30=210mm
    df=m（Z－2.5）=7（30－2.5）=192.5mm
    h=ha+hf=2.25m=15.75mm

  • 第8题：

    已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式△=0，则说明两圆弧（）。

    • A、有两个交点
    • B、相切
    • C、没有交点
    • D、无法判断

    正确答案:B

  • 第9题：

    已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式Δ=0，则说明两圆弧（）。

    • A、有一个交点
    • B、相切
    • C、没有交点
    • D、有两个交点

    正确答案:B

  • 第10题：

    数控编程已知两圆的方程，需联立两圆的方程求两圆交点如果判别式Δ=0，则说明两圆弧（）。

    • A、有一个交点
    • B、相切
    • C、没有交点
    • D、有两个交点

    正确答案:D

  • 第11题：

    "已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式（），则说明两圆弧没有交点。"

    • A、△=0
    • B、△＜0
    • C、△＞0
    • D、不能判断

    正确答案:B

  • 第12题：

    问答题
    已知：AB两端点的坐标值xA=1yA=1和xB=2yB=2，试求直线AB的象限角。

    正确答案： tgα=（yB-yA/xB-xA）=（2-1/2-1）=1
    α=45°
    答：直线AB的象限角为45°。
    解析： 暂无解析

  • 第13题：



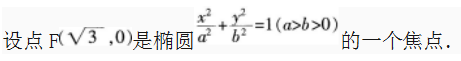
    且与椭圆短轴的两个端点组成等边三角形。
    (1)求椭圆的方程；
    (2)过点F作一直线l交椭圆于A，B两点，设F1为椭圆的另一个焦点，当 △F1AB的面积最大时，求l的方程。


    答案：
    解析：



  • 第14题：

    已知圆O的方程为x2+y2=1，过点P(-2，0)作圆的两条切线，切点分别是A，B，则直线AB的方程是( )。



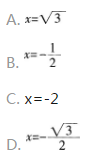    答案：B
    解析：

  • 第15题：

    一对外啮合标准直齿圆柱齿轮，已知模数m=2mm，齿数z1=25，z2=75。求齿距p，全齿高h，分度圆直径d1，d2，齿顶圆直径da1，齿根圆直径df2，标准中心距a和传动比i。

    略

  • 第16题：

    已知：AB两端点的坐标值xA=1yA=1和xB=2yB=2，试求直线AB的象限角。


    正确答案: tgα=（yB-yA/xB-xA）=（2-1/2-1）=1
    α=45°
    答：直线AB的象限角为45°。

  • 第17题：

    已知内齿轮节圆直径为300mm，齿数为30，求：（1）模数。（2）齿顶圆直径。


    正确答案: （1）m=D节/Z=300/30=10
    （2）D顶=m（Z-1.2）=10（30-1.2）=288mm

  • 第18题：

    已知一对斜齿圆柱齿轮的齿数为z1＝26，z2＝93，法向模量mn＝4mm，螺旋角β＝86°34′，求分度圆直径d1、d2，齿顶圆直径da1、da2，齿根圆直径df1、df2和两轮的中心距a（cosβ＝0.99）


    正确答案: 分度圆直径为：
    d1＝mnz1／cosβ＝4×26／0.99＝105.05（mm）
    d2＝mnz2／cosβ＝4×93／0.99＝375.75（mm）
    齿顶圆直径为：
    da1＝d1＋2ha1＝105.05＋2×1×4＝113.05（mm）
    da2＝d2＋2ha1＝375.75＋2×1×4＝383.75（mm）
    齿根圆直径为：
    df1＝d1－2hf1＝105.05－2×1.25×4＝95.05（mm）
    df2＝d2－2hf2＝375.75－2×1.25×4＝365.75（mm）
    两轮的中心距为：
    a＝（d1＋d2）／2＝（105.05＋375.75）／2＝240.4（mm）

  • 第19题：

    已知相啮合的一对标准直齿圆柱齿轮传动，主动轮转速n1=900r/min，从动轮转速n2=300r/min，中心距a=200mm，模数m=5mm，求齿数z1和z2。计算小齿轮的分度圆的直径d1，齿顶圆直径da1。


    正确答案: 由i12= Z2/Z1 =n1 /n2    得Z2/Z1 =3
    又a =m（z1 +z2）/2所以z1 +z2=80 联立得z1=20  z2=60
    分度圆d1 = mz1=100mm    齿顶圆da1=m（z1+2）=66mm

  • 第20题：

    已知蜗轮节圆直径为240mm，模数为6，求：（1）齿顶圆直径。（2）齿根圆直径。


    正确答案: （1）D顶=D节+2m=240+2×6=252mm
    （2）D根=D节-2.4m=240-2.4×6=225.6mm

  • 第21题：

    已知两圆的方程，需联立两圆的方程求两圆交点，如果判别式＞0，则说明两圆弧有一个交点。


    正确答案:错误

  • 第22题：

    在同一平面内，直线与圆弧相切，计算切点坐标的方法是（）。

    • A、将直线方程与圆方程联立求公共解
    • B、将直线方程代入圆方程求解
    • C、将圆方程代入直线方程求解
    • D、将两个方程相加消元求解

    正确答案:A

  • 第23题：

    有一标准渐开线直齿圆柱齿轮，已知：m=4，齿顶圆直径da=88，试求：分度圆直径d=？


    正确答案:d=mz=4×20=80

  • 第24题：

    问答题
    已知一对斜齿圆柱齿轮的齿数为z1＝26，z2＝93，法向模量mn＝4mm，螺旋角β＝86°34′，求分度圆直径d1、d2，齿顶圆直径da1、da2，齿根圆直径df1、df2和两轮的中心距a（cosβ＝0.99）

    正确答案： 分度圆直径为：
    d1＝mnz1／cosβ＝4×26／0.99＝105.05（mm）
    d2＝mnz2／cosβ＝4×93／0.99＝375.75（mm）
    齿顶圆直径为：
    da1＝d1＋2ha1＝105.05＋2×1×4＝113.05（mm）
    da2＝d2＋2ha1＝375.75＋2×1×4＝383.75（mm）
    齿根圆直径为：
    df1＝d1－2hf1＝105.05－2×1.25×4＝95.05（mm）
    df2＝d2－2hf2＝375.75－2×1.25×4＝365.75（mm）
    两轮的中心距为：
    a＝（d1＋d2）／2＝（105.05＋375.75）／2＝240.4（mm）
    解析： 暂无解析

相关内容