20 (本小题满分13分)已知椭圆C的中心在原点,焦点在x 轴上,以两个焦点和短轴的两个端点为顶点的圆边形是一个面积为8的正方形(记为Q)(1) 求椭圆C的方程:
题目
20 (本小题满分13分)
已知椭圆C的中心在原点,焦点在x 轴上,以两个焦点和短轴的两个端点为顶点的圆边形是一个面积为8的正方形(记为Q)
(1) 求椭圆C的方程:
相似考题
更多“20 (本小题满分13分) 已知椭圆C的中心在原点,焦点在x 轴上,以两个焦点和短轴的两个端点为顶点的 ”相关问题
-
第1题:
椭圆x2+2y2=4的四个顶点坐标分别为,长轴长为,短轴长为,焦距为。答案:解析: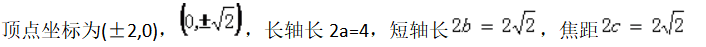
-
第2题:
已知椭圆C的中心在原点,焦点F1.F2在x轴上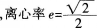 且经过点
且经过点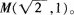
(1)求椭圆C的方程;
(2)如图所示,若直线Z经过椭圆C的右焦点F2且与椭圆C交于A,B两点,使得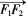
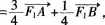 求直线l的方程。
求直线l的方程。 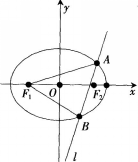 答案:解析:(1)
答案:解析:(1)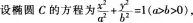

(2)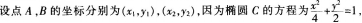
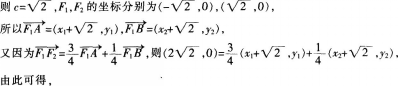

-
第3题:
在2维的坐标系中,距离原点的ℓ_1范数距离(曼哈顿距离)等于1的点的轨迹是____。
A.以原点为中心,半径为1的圆
B.以原点为中心,边长为2,各个边与坐标轴平行的正方形
C.以原点为中心,以两个坐标轴为对角线,边长为根号2的正方形
D.以原点为中心,边长为根号2,各个边与坐标轴平行的正方形
以原点为中心,以两个坐标轴为对角线,边长为根号2的正方形 -
第4题:
已知直线在x轴上的截距为-1,在y轴上的截距为1,又抛物线y=x2+bx+c的顶点坐标为(2,-8),求直线和抛物线两个交点横坐标的平方和.答案:解析:
设直线与抛物线两交点的横坐标为x1和x2,则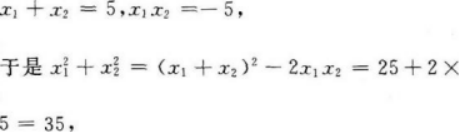
即直线与抛物线两交点的横坐标的平方和为35. -
第5题:
 (1)证明,的中心为原点,并求T的长轴和短轴的长度;(3分)
(1)证明,的中心为原点,并求T的长轴和短轴的长度;(3分)
(2)证明:任给一个椭圆,存在参数R和k,使得T与给定椭圆全等。(4分)答案:解析:(1)由已知得,椭圆Γ为圆柱x2+y2=R2与平面z=kx相交所得,因为圆柱x2+y2=R2和平面z=kx的中心都为原点.故椭圆Γ的中心为原点。
