一列数，前3个是1，9，9，以后每个都是它前面相邻3个数字之和除以3所得的余数，这列数中的第1999个数是几?（　　）A.9 B.0 C.1 D.2

题目
一列数，前3个是1，9，9，以后每个都是它前面相邻3个数字之和除以3所得的余数，这列数中的第1999个数是几?（　　）

A.9
B.0
C.1
D.2
相似考题

1.有一列数，第一个数是90，第二个数是80。从第三个数开始，每一个数都是它前面两个数的平均数。则第100个数的整数部分是（ ）。A．80B．83C．85D．87

2.：有一列数，第1个数是35，第2个数是25，从第3个数开始，每个数都是它前面两个数的平均数。这列数的第15个数的整数部分是（ ）。A．19B．24C．28D．30

3.：一列数1，2，4，7，11，16，22，29，…这列数的组成规律是第2个数比第1个数多1；第3个数比第2个数多2；第4个数比第3个数多3；依此类推。那么这列数左起第1992个数除以5的余数是（ ）。A．0B．1C．2D．4

4.已知数串1，1，2，3，5，8，13，……，从第3个数起每个数都等于它前面相邻的两个数之和，那么，数串中第1999个数被3除所得的余数是（）。A．1B．2C．3D．4

参考答案和解析
答案：B
解析：
将这列数从前至后开始排列：1，9，9，1，1，2，1，1，1，O，2，0，2，1，0，0，1，1，…，这列数除去前面的三个数，其余每13个数为一周期。而(1999-3)÷13=153……7，周期中第7个数是0。所以选B。
更多“一列数，前3个是1，9，9，以后每个都是它前面相邻3个数字之和除以3所得的余数，这列数中的第1999个数是几?（　　）”相关问题

  • 第1题：

    在一列数2，2，4，8，2…中，从第三个数开始，每个数都是它前面两个数乘积的个位数，按照这个规律，这列数中的第2008个应该是( )。

    A．6

    B．4

    C．8

    D．2


    正确答案：C
    C [解析]先将这一列数字延长：2，2，4，8，2，6，2，2，4，8，2，6，2，2…可见这是一个六位循环数列，每个周期是2，2，4，8，2，6。2008÷6=334…4，即前2008个数字中包含334组完整的周期和4个余下的数，那么第2008个数与数列的第4个数相同，为8，答案为C。

  • 第2题：

    34·有一串自然数，已知第一个数与第二个数互质，而且第一个数的恰好是第二个数的，从第三个数开始，每个数字正好是前两个数的和，则这串数的第2005个数被3除所得的余数是( )。

    A.2 .

    B．1

    C．0

    D．3


    正确答案：C
    34．C[解析]第一个数的等于第二个数的则可知第一个数与第二个数之比为3：10，由于这两个数互质，所以第一个数为3，第二个数为l0，从而这串数为3，l0，13，23，36，59，95，154，249，403，652，1055，?被3除的余数是：0，1，1，2，0，2，2，1，0，1．1，2，?按“0，1，1，2，0，2，2，1”循环。因为2005÷8—250余5，所以第2005个数被3除所得的余数应该是第251个周期中的第5个数，即．0。

  • 第3题：

    有一列数：3，7．10，17，27，44-从第三个数起，每个数都等于它前面两个数的和，那么第1998个数除以5的余数是多少？( )

    A，4

    B．3

    C．2

    D．0


    正确答案：D
    D【解析】我们将这列数每个数分别被5除，观察余数有什么规律。这列数每个数分别被5除所得的余数依次是：3，2，0．2，2，4，1，0，1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，…… 从上述结果可知，余数每20个数出现一周期循环。那么有：1998÷20一99……18，而一周期中第18个数是0，所以第1998个数被5除余数是0。故答案为D．

  • 第4题：

    有一个数，除以3余数是2，除以4余数是1。问这个数除以12余数是几？（ ）


    正确答案：B

  • 第5题：

    1，1995，1994，1，1993，1992，…，从第三个数起，每个数都是它前面两个数中大数减小数的差。则这列数中前1995个数的和是（　　）。

    A.1769565
    B.1770225
    C.1770230
    D.1769566

    答案：C
    解析：
    前1995个数中有1995÷3=665个1，其余的1995-665=1330个数是自然数666～1995，它们的和是(666+1995)×1330÷2=1769565，所以前l995个数的和是1769565+665=1770230。

  • 第6题：

    如图，有一个11位数，它的每3个相邻数字之和都是20，则标有*的那个数位上的数字应是几？


    A.9
    B.7
    C.5
    D.3

    答案：B
    解析：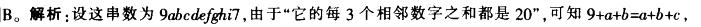

  • 第7题：

    1，1995，1994，1，1993，1992，…，从第三个数起，每个数都是它前面两个数中大数减小数的差。则这列数中前1995个数的和是（）。

    • A、1769565
    • B、1770225
    • C、1770230
    • D、1769566

    正确答案:C

  • 第8题：

    单选题
    有一个数，除以3余数是2，除以4余数是1。问这个数除以12余数是几？（....）
    A

    4

    B

    5

    C

    6

    D

    7


    正确答案： C
    解析：

  • 第9题：

    单选题
    在一列数2、2、4、8、2…中，从第三个数开始，每个数都是它前面两个数乘积的个位数，按照这个规律，这列数中的第2008个数应该是（　　）。
    A

    6

    B

    4

    C

    8

    D

    2


    正确答案： C
    解析：
    先将这一列数字延长：2、2、4、8、2、6、2、2、4、8、2、6、2、2…可见这是一个六位循环数列，每个周期是2、2、4、8、2、6。2008÷6＝334余4，即前2008个数字中包含334组完整的周期和4个数，那么第2008个数与第335组周期中的第4个数相等，为8。

  • 第10题：

    单选题
    8个自然数按顺序排列在一起，从第3个数开始，每个数都是前面2数之和，第5个数是7，第8个数是几？（）
    A

    11

    B

    18

    C

    29

    D

    47


    正确答案： A
    解析： 暂无解析

  • 第11题：

    有一列数：3，7，10，17，27，44，…从第三个数起，每个数都等于它前面两个数的和，那么第1998个数除以5的余数是（ ）。

    A．4

    B．3

    C．2

    D．0


    正确答案：D
    【解析】我们将这列数每个数分别被5除，观察余数有什么规律。这列数每个数分别被5除所得的余数依次是：3，2，0，2，2，4，1，0，1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，…从上述结果可知，余数每20个数出现一周期循环。那么有：1998÷20＝99…18，而一个周期中第18个数是0，所以第1998个数袖5除余数是0。

  • 第12题：

    在一列数2、2、4、8、2…中，从第三个数开始，每个数都是它前面两个数乘积的个位数，按照这个规律，这列数中的第2008个数应该是( )。

    A．6

    B．4

    C．8

    D．2


    正确答案：C
    C [解析]先将这一列数字延长：2、2、4、8、2、6、2、2、4、8、2、6、2、2…可见这是一个六位循环数列，每个周期是2、2、4、8、2、6。2008÷6=334…4，即前2008个数字中包含334组完整的周期和4个数，那么第2008个数与第335组周期中的第4个数相等，为8，答案为C。

  • 第13题：

    70个数排成一列．除了两头的两个数以外，每个数的3倍都恰好等于它两边两个数的和，这一列数最左边的几个是这样的∶0、l、3、8、21、……，问最右边的一个数被6除余几?

    A．3

    B．4

    C．5

    D．1


    正确答案：B
    ．【答案】B。解析∶这些数是0、1、3、8、21、55、144、377、987、……它们除以6得到余数是∶0、1、3、2、3、1、0、5、3、4、3、5、……把这列数写出一部分，可发现它们除以6的余数的周期数是12，70＋12=5……10，第10个余数是4，所以余4。

  • 第14题：

    有一列数：3，7，10，17，27，44…从第三个数起，每个数都等于它前面两个数的和，那么第1998个数除以5的余数是多少？（ ）

    A. 4

    B. 3

    C. 2

    D. 0


    正确答案：D
    D［解析］我们将这列数每个数分别被5除，观察余数有什么规律。
    这列数每个数分别被5除所得的余数依次是：
    3，2，0，2，2，4，1，0，1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，…
    从上述结果可知，余数每20个数出现一周期循环。那么有：1998÷20=99……18,而一周期中第18个数是0，所以第1998个数被5除余数是0；

  • 第15题：

    有68个数排成一排，除头为两个数外，每个数的3倍恰好等于他两边两个数之和。经分析发现，这些数除以6所得的余数以12个数为周期重复出现。已知前两个数是0和1，则该数列最后一个数除以6的余数是（）。


    A. 2
    B. 3
    C. 4
    D. 5

    答案：D
    解析：
    解题指导： 68/12=5余8 所以是5个周期后的第八个数 0，1，3，8，21，55，144，377 377/6=62余5，就是5。故答案为D。

  • 第16题：

    8个自然数按顺序排列在一起，从第3个数开始，每个数都是前面2数之和，第5个数是7，第8个数是几？（）

    • A、11
    • B、18
    • C、29
    • D、47

    正确答案:C

  • 第17题：

    有一串数：1，3，8，22，60，164，448，……；其中第一个数是1，第二个数是3，从第三个数起，每个数恰好是前两个数之和的2倍。那么在这串数中，第2000个数除以9的余数是（）。

    • A、1
    • B、2
    • C、3
    • D、4

    正确答案:C

  • 第18题：

    单选题
    有一个数，甲将其除以6，乙将其除以7，甲所得的商与乙所得的余数之和为12，则甲所得的余数为（　　）。
    A

    3

    B

    4

    C

    5

    D

    6


    正确答案： D
    解析：
    设甲所得的商和余数分别为a和b，乙所得的商和余数分别为c和d，则有①6a＋b＝7c＋d，②a＋d＝12。将d＝12－a代入①得：7（a－c）＝12－b。左端是7的倍数，因此12－b也是7的倍数。由于b是被6除的余数，即b介于0与5之间，得b＝5。

  • 第19题：

    单选题
    一列数，前3个是1，9，9，以后每个都是它前面相邻3个数字之和除以3所得的余数。这列数中的第1999个数是几？（　　）
    A

    9

    B

    0

    C

    1

    D

    2


    正确答案： D
    解析：
    将这列数依次排列得1，9，9，1，1，2，1，1，1，0，2，0，2，1，0，0，1，1，……除去前面的三个数，其余以每13个数为周期循环，而（1999－3）÷13＝153……7，即周期中第7个数是0。

相关内容