用1、2、3、4这4个数字任意写出一个一万位数,从这个一万位数中任意截取相邻的个数字,可以组成许多四位数,这些四位数中,至少有多少个相同?A.39 B.40 C.41 D.42
题目
B.40
C.41
D.42
相似考题
更多“用1、2、3、4这4个数字任意写出一个一万位数,从这个一万位数中任意截取相邻的个数字,可以组成许多四位数,这些四位数中,至少有多少个相同?”相关问题
-
第1题:
从0,1,2,7,9五个数字中任选四个不重复的数字,组成的最大四位数和最小四位数的差是( )。
A.8442
B.8694
C.8740
D.9694
正确答案:B
由题意可知,最大的四位数为9721,最小的四位数为1027,所以两者的差是9721-1027=8694。故本题选B。 -
第2题:
从数字0、1、2、3、4、5中任意挑选5个组成能被5除尽且各位数字互异的五位数,那么共可以组成多少个不同的五位数?( ) A.120 B.96 C.20 D.216
D.只需用考虑这个五位数的个位上是0或5的情况,为0的时候,有5*4*3*2=120中方法;为5的是候,万位上不能为0,则有4*4*3*2=96种,加起来选D。
-
第3题:
从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为
(A)432 (B)288 (C) 216 (D)108
正确答案:C
-
第4题:
173□是个四位数,小明在这个□中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除。问:小明先后填入的3个数字的和是多少?A.19
B.21
C.23
D.17答案:A解析:1730分别除以9、11、6,余数为2、3、2。因此个位需要分别加上9-2=7,11-3=8,6-2=4,才能保证被9、11、6整除。则这3个数之和为7+8+4=19。 -
第5题:
桌子上有数字标签四个,数字分别是2、5、8和9,用这个数字标签随意摆放,组成一个四位数, 将每一个四位数记录下来,按照从小到大的顺序排列,则排在第8位的四位数是()。A.5289
B.5298
C.2985.
D.5829答案:B解析:首先当2为首位的时候,后面三个数字全排列的方式有A(3,3)-6种,则可知排在第8位的数字应是5为首位时从小到大排在第二的数字,5为首位时,从小到大排列,最小的数字第二位应是2。第三位8,第四位9,其次小的是第一位s,第二位2,第三位9,第四位8,这是应是总体排在第8位的四位数,即5298,B选项正确,A. C. D选项错误。故本题应选B. -
第6题:
从数字0,1,2,3中任意选择组合,可以得到多少个所含数字不重复的偶数。
A. 27
B. 17
C. 7
D. 32答案:A解析:解题指导: 1位数 0 ,2;2位数 当个位是0 ,有3个;个位是2,有2个;3位数 当个位是0,有6个;个位是2,有4个;4位数 当个位是0,有6个;个位是2,有4个;因此一共有27个。故答案为A。 -
第7题:
用1、2、3、4这4个数字任意写出一个一万位数,从这个一万位数中任意截取相邻的4个数字,可以组成许多四位数,这些四位数中,至少有多少个相同?( )A.39
B.40
C.41
D.42答案:B解析:
-
第8题:
用数字0,1,2,3,4,5组成没有重复数字的四位数,其中三个偶数连在一起的四位数有多少个( )A.20
B.28
C.30
D.36
E.40答案:C解析:
-
第9题:
一个密码由4位不相同的数字组成,已知由这四个数字按次序组成的阿拉作?数字小于2000,且第二位数比第四位数大7。问满足这一条件的密码一共有多少个?A.28
B.36
C.60
D.120答案:A解析:本题考查排列组合问题。
密码按次序组成的4位数小于2000,第一位只能是0或1。第二位比第四位大7,只能是(7、0),(8、1),(9、2)三个组合中的一种。要求不重复,则第一位有两种选法,选择后第二位、第四位总共只能有两种选法,第三位可以在剩余10-3=7个数字里任意挑选。分步用乘法,有2×2×7=28(种)。
故本题的正确答案为A项。 -
第10题:
单选题1730是个四位数,小明在这个数中先后填入3个数字,所得到的3个四位数,依次可被9、11、6整除。问:小明先后填入的3个数字的和是多少?( )A19
B21
C23
D17
正确答案: B解析:
1730分别除以9、11、6,余数为2、3、2。因此个位需要分别加上9-2=7、11-3=8、6-2=4才能保证被9、11、6整除。则这3个数之和为7+8+4=19。 -
第11题:
用2、4、5、7这4个不同数字可以组成24个互不相同的四位数,将它们从小到大排列,那么7254是第多少个数?( )
A.19
B.20
C.18
D.17
正确答案:B
B【解析】由已知得每个数字开头的数各有24÷4=6个,从小到大排列,7开头的从第6×3+1=19个开始,易知第19个是7245,第20个是7254。故答案为B.
-
第12题:
从0,1,2,3,4,5这六个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数的个数为
(A)300 (B)216 (C) 180 (D)162
正确答案:C
-
第13题:
用1,2,3,4这4个数字任意写出一个10000位数,从这个10000位数中任意截取相邻的4个数字,可以组成许许多多的四位数。这些四位数中至少有多少个是相同的?( )A. 40
B. 64
C. 256
D. 30答案:A解析:本题实际上是抽届原理的考查,物品应是截取出的所有四位数,而将不同的四位数作为抽屉。在10000位数中,共能截取出相邻的四位数:
10000-3 = 9997(个),即物品数是9997。
用1,2,3,4这四个数字可以组成的不同四位数,根据乘法原理有:
4X4X4X4 = 256(种)
这就是说有256个抽屉。
9997/256 = 39......13
所以这些四位数中,至少有40个是相同的。 -
第14题:
一个四位数与7的和是由没有重复数字组成的最小四位数,问原四位数的个位是多少?( )A. 3
B. 4
C. 5
D. 6答案:D解析:设这个四位数为x
则x+7=1023
x=1016
这个四位数的个位数是6 这个四位数是1016 -
第15题:
一个7层楼的酒店,每层有20间客房。酒店的房间号为一个3位数字,其中第一位为楼层,第二、三位为从01到20的房间编号。相邻的房间房号也相邻。某个楼层三个相邻房间的房号之和为一个各位数字均不相同、且各位数字之和为6的四位数。则这三个相邻房间的房号组合有多少种不同的可能 《》( )A.2
B.1
C.6
D.4答案:A解析:房号之和为一个各位数字均不同,且各位数字之和为6的四位数。故这四个数字只能是0、1、2、3。分情况讨论:
①假设三个相邻房间号的和为1023,则中间房间的房号是1023+3=341,因房间的编号是01-20,故后两位数字不可能是41,排除;
②假设房号之和为1032,中间房间的房号是1032÷3=344,排除;
③假设房号之和为1203,中间房间的房号是1203÷3=401, 401 一定是第一间房,不可能是中间的房间,
排除;
④假设房号之和为1230,中间房间的房号是1230÷3= 410,则连续的三间房是409、410、 411, 符合;
⑤假设房号之和为1302,中间房间的房号是1302÷3= 434,排除;
⑥假设房号之和为1320,中间房间的房号是
1320+3= 440, 排除:
⑦假设房号之和分别为2013、2031、 2103,则中间房间的房号分别是671、677、 701, 都不满足,排除;
⑧假设房号之和分别为2130、2301、 2310,则中间房间的房号分别是710、767、 770, 只有710满足;
⑨假设房号之和为3012,则中间房间的房号- -定为4位数字,故房号之和不可能是3开头的四位数,排除。
则三间连续的房间为409、410、 411 或者709、710、 711 两种情况。
故正确答案为A。 -
第16题:
用2012减去一个四位数的差,正好等于将这个四位数各个数位数字相加的和,那么有几个这样的四位数?( )
A. 1
B. 2
C. 3
D. 4答案:A解析:大于2000的数,经检验只有2005符合题目要求。小于2000的数,则这个四位数的前两位是1和9。取数字1996验证,2012 -1996 = 26。1+9 + 9 + 6 = 25。当这个四位数增大1时,2012与这个四位数的差会少1,因此小于2000的数中没有符合题目要求的。故有1个这样的四位数。 -
第17题:
从0,2,4,6中取出3个数字,从1,3,5,7中取出两个数字,共能组成多少个没有重复数字且大于65000的五位数答案:解析:根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型.
(1)能组成7××××型的五位数的个数是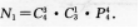
(2)能组成65×××型的五位数的个数是
(3)能组成67×××型的五位数的个数是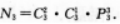
故所求的五位数的个数为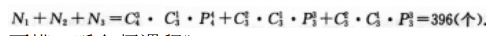
-
第18题:
由20×20的小方格组成一个大正方形,从1~9这9个数字中任意选出一个数字填入每个小方格。把其中任意一个田字格图形中的4个数相加,均能得到一个和数。请问所能得到的和数中,至少有( )个是相同的。A.11
B.20
C.33
D.36答案:A解析:第一步,本题考查最值问题,用极值思维解题。
第二步,1~9中4个数相加的和数中最小为1+1+1+1=4,最大为9+9+9+9=36,中间每一个都可以取到,则和数的总数为36-4+1=33(个)。
第三步,20×20的小方格可以组成(20-1)×(20-1)=19×19=361(个)田字方格。
第三步,要使相同和数个数尽量少,则每个和数应尽可能的多,最多的情况为个数都相同,则为
则至少有10+1=11(个)是相同的。 -
第19题:
单选题1997的数字之和是1+9+9+7=26,小于2000的四位数中,数字之和为26的数除1997外还有多少个?( )A3
B4
C5
D6
正确答案: B解析:
将1997变换数位,可得1979和1799;由于千位必须为,则百,十,个位上的数字和为26-1=25,又数位上的数最大是9,则只能为8,8,9,组成四位数1889,1898和1988。即一共有5个数。 -
第20题:
单选题从0,1,2,7,9五个数字中任选四个不重复的数字,组成的最大四位数和最小四位数的差是()。A8442
B8694
C8740
D9694
正确答案: D解析: 暂无解析
