下列命题中,哪个是正确的? A.周期函数f(x)的傅立叶级数收敛于f (x) B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)D.正项级数收敛的充分且“条件是级数的部分和数列有界
题目
下列命题中,哪个是正确的?
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
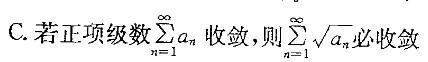
D.正项级数收敛的充分且“条件是级数的部分和数列有界
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
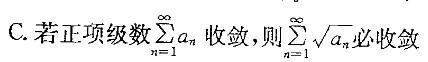
D.正项级数收敛的充分且“条件是级数的部分和数列有界
相似考题
参考答案和解析
答案:D
解析:
提示:本题先从熟悉的结论着手考虑,逐一分析每一个结论。选项D是正项级数的基本定理,因而正确,其余选项均错误。选项A,只在函数的连续点处级数收敛于f(x);选项B,级

更多“下列命题中,哪个是正确的? A.周期函数f(x)的傅立叶级数收敛于f (x) B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x) D.正项级数收敛的充分且“条件是级数的部分和数列有界”相关问题
-
第1题:
设f(x)是以2π为周期的周期函数,在[-π,π)上的表达式为f(x)=x,则f(x)的傅里叶级数为( ).A.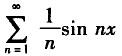
B.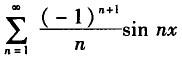
C.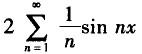
D.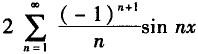 答案:D解析:
答案:D解析: -
第2题:
若级数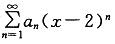 在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?
A.发散
在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?
A.发散
B.条件收敛
C.绝对收敛
D.收敛性不能确定答案:C解析:提示:设:x-2 = z,级数化为 ,当x=-2收敛,即z=-4收敛,利用阿贝尔定理z在(-4,4)收敛且绝对收敛,当时,x=5时,z=3所以级数收敛且绝对收敛,答案选C。
,当x=-2收敛,即z=-4收敛,利用阿贝尔定理z在(-4,4)收敛且绝对收敛,当时,x=5时,z=3所以级数收敛且绝对收敛,答案选C。 -
第3题:
设任意项级数 ,若
,若 ,且
,且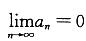 ,则对该级数下列哪个结论正确?
A.必条件收敛
,则对该级数下列哪个结论正确?
A.必条件收敛
B.必绝对收敛
C.必发散
D.可能收敛,也可能发散答案:D解析:提示:举例说明,级数 均满足条件,但前面级数发散,后面级数收敛,敛散性不能确定。
均满足条件,但前面级数发散,后面级数收敛,敛散性不能确定。 -
第4题:
设f(x)是以2π为周期的周期函数,在[-π,π]上的表达式为f(x)=cos(x/2),则f(x)的傅里叶级数为( ).A.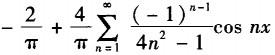
B.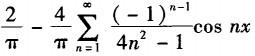
C.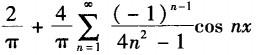
D. 答案:C解析:
答案:C解析:
-
第5题:
数项级数的部分和数列有界是该级数收敛的( ).A.充分条件
B.必要条件
C.充分必要条件
D.既非充分又非必要条件答案:B解析:按数项级数收敛的定义,级数收敛即级数的部分和数列有极限,而部分和数列有界 是部分和数列有极限的必要条件,故选B. -
第6题:
若级数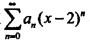 在x = -2处收敛,则此级数在x= 5处( )。
在x = -2处收敛,则此级数在x= 5处( )。
A.发散 B.条件收敛 C.绝对收敛 D.收敛性不能确定答案:C解析:提示:利用阿贝尔定理,级数在(-2,6)内绝对收敛。 -
第7题:
将函数f(x)=xe3x展开为x的幂级数,并指出其收敛区间.答案:解析:
-
第8题:
函数f(x)=x/(x2-5x+6)展开成(x-5)的级数的收敛区间是()
- A、(-1,1)
- B、(-1,1)
- C、(3,7)
- D、(4,5)
正确答案:C -
第9题:
单选题若级数在x=-2处收敛,则此级数在x=5处()。A发散
B条件收敛
C绝对收敛
D收敛性不能确定
正确答案: D解析: 暂无解析 -
第10题:
单选题下列命题中,错误的是().A部分和数列{s}有界是正项级数收敛的充分条件
B若级数绝对收敛,则级数必定收敛
C若级数条件收敛,则级数必定发散
D若,则级数收敛
正确答案: A解析: 暂无解析 -
第11题:
若级数

在x=-2处收敛,则此级数在x=5处的敛散性是( )。
A.发散
B.条件收敛
C.绝对收敛
D.收敛性不能确定答案:C解析:设x-2=z,利用可贝尔定理判定 -
第12题:
设函数f(x)在(-∞,+∞)内单调有界,{xn}为数列,下列命题正确的是
A.若{xn}收敛,则{f(xn)}收敛
B.若{xn}单调,则{f(nx)}收敛
C.若{f(xn)}收敛,则{xn}收敛
D.若{f(xn)}单调,则{xn}收敛答案:B解析:(方法一)由于{xn}单调,f(xn)单调有界,则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛,故应选(B). (方法二)排除法:若取 ,则显然f(xn)单调,{xn}收敛,但显然{f(xn)}不收敛,这样就排除了(A).若取f(xn)=arctanx,x=n,则f(xn)=arctann,显然{f(xn)}收敛且单调,但{xn}不收敛,这样就排除了(C)和(D),故应选(B).
,则显然f(xn)单调,{xn}收敛,但显然{f(xn)}不收敛,这样就排除了(A).若取f(xn)=arctanx,x=n,则f(xn)=arctann,显然{f(xn)}收敛且单调,但{xn}不收敛,这样就排除了(C)和(D),故应选(B). -
第13题:
下列命题中,哪个是正确的?A.周期函数f(x)的傅立叶级数收敛于f(x)
B.若f(x)有任意阶导数,则f(x)的泰勒级数收敛于f(x)
C.若正项级数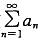 收敛,则
收敛,则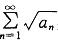 必收敛
必收敛
D.正项级数收敛的充分且必-条件是级数的部分和数列有界答案:D解析:提示:本题先从熟悉的结论着手考虑,逐一分析每一个结论。选项D是正项级数的基本定理,因而正确,其余选项均错误。选项A,只在函数的连续点处级数收敛于f(x);选项B,级数收敛,还需判定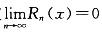 ;选项C,可通过举反例说明,级数
;选项C,可通过举反例说明,级数 收敛,但
收敛,但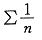 发散。
发散。 -
第14题:
下列命题中,错误的是( ).A.设f(x)为奇函数,则f(x)的傅里叶级数是正弦级数
B.设f(x)为偶函数,则f(x)的傅里叶级数是余弦级数
C.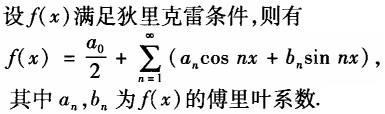
D.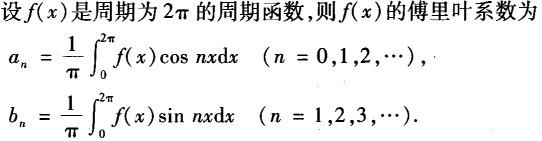 答案:C解析:
答案:C解析:
-
第15题:
若幂级数 在x=-2处收敛,在x = 3处发散,则该级数( )。
在x=-2处收敛,在x = 3处发散,则该级数( )。
A.必在x = -3处发散 B.必在x=2处收敛
C.必在 x >3时发散 D.其收敛区间为[-2,3)答案:C解析:提示:利用阿贝尔定理。 -
第16题:
将f(x)=1/(2-x)展开为x的幂级数,其收敛域为( )。
A. (-1,1) B. (-2,2) C.〔-1/2,1/2) D. (-∞,+∞)答案:B解析:
-
第17题:
设幂级数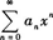 在x=2处收敛,则该级数在x=-1处必定().A.发散
在x=2处收敛,则该级数在x=-1处必定().A.发散
B.条件收敛
C.绝对收敛
D.敛散性不能确定答案:C解析:
-
第18题:
下列命题中,错误的是().
- A、部分和数列{s}有界是正项级数收敛的充分条件
- B、若级数绝对收敛,则级数必定收敛
- C、若级数条件收敛,则级数必定发散
- D、若,则级数收敛
正确答案:D -
第19题:
单选题若级数[v]在x=-2处收敛,则此级数在x=5处的敛散性是怎样的?()A发散
B条件收敛
C绝对收敛
D收敛性不能确定
正确答案: B解析: 暂无解析 -
第20题:
单选题设函数f(x)在(-∞,+∞)内单调有界,{xn}为数列,下列命题正确的是( )。A若{xn}收敛,则{f(xn)}收敛
B若{xn}单调,则{f(xn)}收敛
C若{f(xn)}收敛,则{xn}收敛
D若{f(xn)}单调,则{xn}收敛
正确答案: D解析:
由题意知,若{xn}单调,则{f(xn)}单调有界,则{f(xn)}一定存在极限,即{f(xn)}收敛。
