设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为：若将f(x)展开成傅里叶级数，则该级数在x=-3π处收敛于( )。
题目
设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为：
若将f(x)展开成傅里叶级数，则该级数在x=-3π处收敛于( )。
若将f(x)展开成傅里叶级数，则该级数在x=-3π处收敛于( )。
相似考题
参考答案和解析
答案：C
解析：
所给函数满足收敛定理，当x=-3π为函数的问断点，函数f(x)的傅里叶级数在x
更多“设f(x)是周期为2π的周期函数，它在[-π，π]上的表达式为： ”相关问题
-
第1题：
当X>0时,f(x)=5x²＋2是()A、增函数
B、减函数
C、周期函数
D、奇函数
参考答案：A
-
第2题：
设f(x)是以2π为周期的周期函数，在[-π，π]上的表达式为f(x)=cos(x/2)，则f(x)的傅里叶级数为( ).A.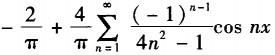
B.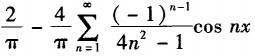
C.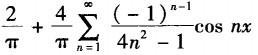
D.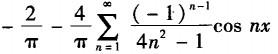
答案：C解析：
-
第3题：
设F(x)是连续函数f(x)的一个原函数，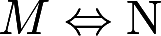
表示“M的充分必要条件是N”，则必有
AF(x)是偶函数
f(x)是奇函数
BF(x)是奇函数
f(x)是偶函数
CF(x)是周期函数
f(x)是周期函数
DF(x)是单调函数
f(x)是单调函数答案：A解析：
-
第4题：
A.是周期函数，且周期为π
B.是周期函数，且周期为2π
C.是周期函数，且周期为3π
D.不是周期函数答案：B解析：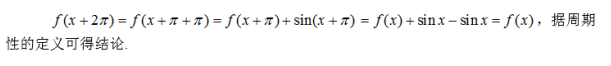
-
第5题：
设F（x）是连续函数f（x）的一个原函数，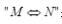
表示“M的充分必要条件是N”，则必有（ ）。A．F（x）是偶函数f（x）是奇函数
B．F（x）是奇函数f（x）是偶函数
C．F（x）是周期函数f（x）是周期函数
D．F（x）是单调函数f（x）是单调函数答案：A解析：
-
第6题：
设f(x)是周期为4的可导奇函数，且f'(x)=2(x-1)，x∈［0，2］，则f(7)=________.答案：1、1.解析：由f'(x)=2(x-1)，x∈［0，2］知，f(x)=(x-1)^2+C.又f(x)为奇函数，则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期，则f(7)=f［8+(-1)］=f(-1)=-f(1)=1. -
第7题：
设f(x)是以7为周期的偶函数，且f(－2)＝5，则f(9)＝（ ）A.－5
B.5
C.－10
D.10答案：B解析：因为f(x)是偶函数，所以f(2)＝f(－2)＝5，又因为f(x)是以7为周期的函数，则f(9)＝f(7＋2)＝f(2)＝5．(答案为B) -
第8题：
设f(x)是连续函数，F(x)是f(x)的原函数，则（）。
A.当f(x)是奇函数时，F(x)必是偶函数
B.当f(x)是偶函数时，F(x)必是奇函数
C.当f(x)是周期函数时，F(x)必是周期函数
D.当f(x)是单调增函数时，F(x)必是单调增函数答案：B解析：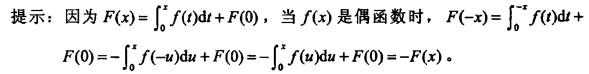
-
第9题：
设函数y=f(x)为最小正周期为π的奇函数，则f(x)可能是( )。A.f(x)=sinx
B.f(x)=tan2x
C.f(x)=sin(2x+π/2)
D.f(x)=sinxcosx答案：D解析：
-
第10题：
单选题若f（x）是在（－∞，＋∞）内可导的以l为周期的周期函数，则f′（ax＋b）（a≠0，a、b为常数）的周期为（ ）。Al
Bl－b
Cl/a
Dl/｜a｜
正确答案： A解析：
f（x）与f′（x）具有相同的周期。由f（x）的周期为l，可以推知f（ax＋b）的周期为l/｜a｜，故f′（ax＋b）的周期也是l/｜a｜。 -
第11题：
单选题设在区间（－∞，＋∞）内函数f（x）＞0，且当k为大于0的常数时有f（x＋k）＝1/f（x）则在区间（－∞，＋∞）内函数f（x）是（ ）。A奇函数
B偶函数
C周期函数
D单调函数
正确答案： C解析：
对该函数由f（x＋2k）＝1/f（x＋k）＝f（x），故f（x）是周期函数。 -
第12题：
单选题若f（x）是以l为周期的连续函数，则其原函数（ ）。A是以l为周期的函数
B是周期函数，但周期不是l
C不是周期函数
D不一定是周期函数
正确答案： D解析：
举反例：f（x）＝1＋cosx是一个以2π为周期的函数，但是∫f（x）dx＝∫（1＋cosx）dx＝x＋sinx＋C不是周期函数，但若f（x）＝cosx，则∫f（x）dx＝sinx是以2π为周期的函数。 -
第13题：
请教:2008 年春季中国精算师资格考试－01数学基础(一)第1大题第1小题如何解答?【题目描述】
1．设f(x)为连续函数，F(x)是f(x)的原函数，则（ ）。
(A) 当f(x)是奇函数时，F(x)必为偶函数
(B) 当f(x)是偶函数时，F(x)必为奇函数
(C) 当f(x)是周期函数时，F(x)必为周期函数
(D) 当f(x)是单增函数时，F(x)必为单增函数
(E) 当f(x)是单减函数时，F(x)必为单减函数
正确答案：A
-
第14题：
设f(x)是以2π为周期的周期函数，它在[-π，π)上的表达式为f(x)=|x|，则f(x)的傅里叶级数为( ).A.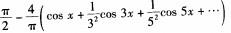
B.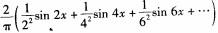
C.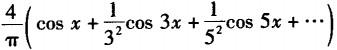
D.
答案：A解析：
-
第15题：
若f（x）是在（-∞，+∞）内可导的以l为周期的周期函数，则f′（ax+b）（a≠0，a、b为常数）的周期为（ ）A.l
B.l-b
C.l/a
D.l/|a|答案：D解析：
-
第16题：
设f(x)是以2π为周期的周期函数，在[-π，π)上的表达式为f(x)=x，则f(x)的傅里叶级数为( ).A.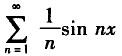
B.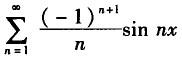
C.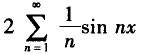
D.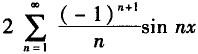
答案：D解析： -
第17题：
设f(x)是连续函数，
(Ⅰ)利用定义证明函数
可导，且F’(x)=f(x)；
(Ⅱ)当f(x)是以2为周期的周期函数时，证明函数
也是以2为周期的周期函数.答案：解析：
-
第18题：
设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.答案：解析：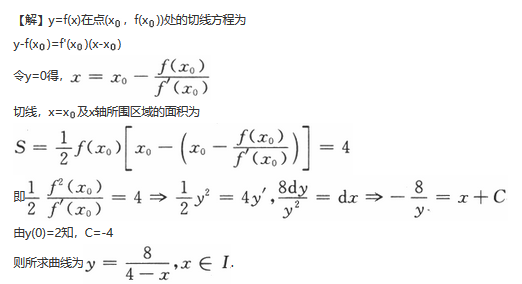
-
第19题：
设函数f(x)在定义域，上的导数大于零，若对任意的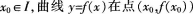
处的切线与直线x≈x0及戈轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式。答案：解析：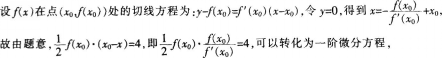
-
第20题：
设f(x)为定义在R上的奇函数，当x≥0时,f(x)=2x+2x+b(b为常数)，则f(-1)=( )。A.3
B.1
C.-1
D.-3答案：D解析：因为设f(x)为定义在R上的奇函数，故f(0)=20+2xO+b=0，得6=-1，即当x≥0时f(x)=2x+2x-1，故，f(1)=21+2x1-1=3，故f(-1)=f(1)=-3。 -
第21题：
在a，b，c坐标中，转子和A相轴线夹角为，下列叙述正确的是：（）。
- A、定子绕组自感系数是α的周期函数，周期为π
- B、定子绕组互感系数是2α的周期函数，周期为π
- C、转子绕组自感系数是α的周期函数，周期为π
- D、转子绕组互感系数是2α的周期函数，周期为π
正确答案:A -
第22题：
单选题f（x）＝|xsinx|ecosx（－∞＜x＜＋∞）是（ ）。A有界函数
B单调函数
C周期函数
D偶函数
正确答案： D解析：
因f（－x）＝|（－x）sin（－x）|ecos（－x）＝f（x），故f（x）为偶函数。 -
第23题：
单选题设F（x）是连续函数f（x）的一个原函数，“M⇔N”表示“M的充分必要条件是N”，则必有（ ）。AF（x）是偶函数⇔f（x）是奇函数
BF（x）是奇函数⇔f（x）是偶函数
CF（x）是周期函数⇔f（x）是周期函数
DF（x）是单调函数⇔f（x）是单调函数
正确答案： C解析：
采用举例的方法进行排除，令f（x）＝x，在（－∞，＋∞）内单调增加，但是F（x）＝x2/2＋C在（－∞，＋∞）内不单调，D项错误；
令f（x）＝x2为偶函数，但是F（x）＝x3/3＋C，其中C≠0时不是奇函数，故B项错误；
令f（x）＝1＋cosx是以2π为周期的函数，但是F（x）＝x＋sinx＋C不是周期函数，故C项错误。