设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是 A.A若{xn}收敛，则{f(xn)}收敛 B.若{xn}单调，则{f(xn)}收敛 C.若{f(xn)}收敛，则{xn}收敛 D.若{f(xn)}单调，则{xn}收敛
题目
设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是
A.A若{xn}收敛，则{f(xn)}收敛
B.若{xn}单调，则{f(xn)}收敛
C.若{f(xn)}收敛，则{xn}收敛
D.若{f(xn)}单调，则{xn}收敛
B.若{xn}单调，则{f(xn)}收敛
C.若{f(xn)}收敛，则{xn}收敛
D.若{f(xn)}单调，则{xn}收敛
相似考题
更多“设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是”相关问题
-
第1题：
设函数f(x)在(-∞，+∞)内单调有界，{xn}为数列，下列命题正确的是
A.若{xn}收敛，则{f(xn)}收敛
B.若{xn}单调，则{f(nx)}收敛
C.若{f(xn)}收敛，则{xn}收敛
D.若{f(xn)}单调，则{xn}收敛答案：B解析：(方法一)由于{xn}单调，f(xn)单调有界，则数列{f(xn)}单调有界.由单调有界准则知数列{f(xn)}收敛，故应选(B). (方法二)排除法：若取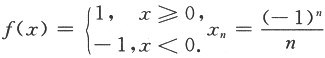
，则显然f(xn)单调，{xn}收敛，但显然{f(xn)}不收敛，这样就排除了(A).若取f(xn)=arctanx，x=n，则f(xn)=arctann，显然{f(xn)}收敛且单调，但{xn}不收敛，这样就排除了(C)和(D)，故应选(B). -
第2题：
下列命题中，错误的是( ).A.设f(x)为奇函数，则f(x)的傅里叶级数是正弦级数
B.设f(x)为偶函数，则f(x)的傅里叶级数是余弦级数
C.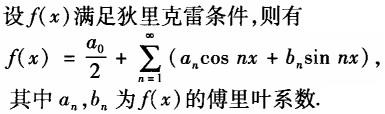
D.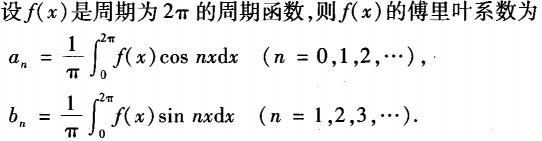
答案：C解析：
-
第3题：
设函数f（x）在x=0处连续，下列命题错误的是（ ）.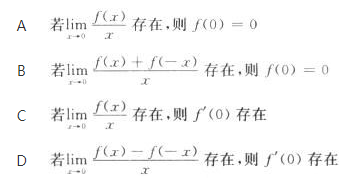
答案：D解析：
-
第4题：
下列命题中，哪个是正确的？
A.周期函数f(x)的傅立叶级数收敛于f (x)
B.若f(x)有任意阶导数，则f(x)的泰勒级数收敛于f(x)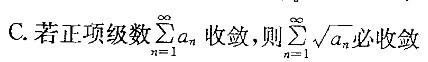
D.正项级数收敛的充分且“条件是级数的部分和数列有界答案：D解析：提示:本题先从熟悉的结论着手考虑，逐一分析每一个结论。选项D是正项级数的基本定理，因而正确，其余选项均错误。选项A，只在函数的连续点处级数收敛于f(x)；选项B，级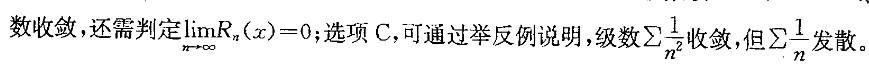
-
第5题：
根据f(x)的导函数f'(x)的图像，判定下列结论正确的是（）
A.在(－∞，－1)内，f(x)是单调增加的
B.在(－∞，0)内，f(x)是单调增加的
C.f(－1)为极大值
D.f(－1)为极小值答案：D解析：x轴上方的f'(x)＞0，x轴下方的f'(x)＜0，即当x＜－1时，f'(x)＜0；当x＞－1时f'(x)＞0，根据极值的第一充分条件，可知f(－1)为极小值，所以选D． -
第6题：
下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数，则f(x)也为单调函数
C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0答案：D解析：可导函数的极值点必定是函数的驻点，故选D. -
第7题：
设函数f(x)在(0，1)内可导，f'(x)>0，则f(x)在(0，1)内（ ）A.单调减少
B.单调增加
C.为常量
D.不为常量，也不单调答案：B解析：由于f'(x)>0，可知f(x)在(0，1)内单调增加．因此选B． -
第8题：
设单调可微函数f(x)的反函数为g(x),f(1)=3,f′(1)=2,f″(3)=6则g′(3)=（）
正确答案:1/2 -
第9题：
单选题设函数在（a，b）内连续，则在（a，b）内（）。Af（x）必有界
Bf（x）必可导
Cf（x）必存在原函数
DD.必存在一点ξ∈（a，，使f（ξ）=0
正确答案： A解析： 暂无解析 -
第10题：
单选题函数f（x）＝[cos（1/x）]/x在x＝0点的任何邻域内都是（ ）。A有界的
B无界的
C单调增加的
D单调减少的
正确答案： B解析：
f（1/（2kπ））＝2kπcos2kπ＝2kπ，其中，k＝±1，±2，…，故f（x）在x＝0点的任何邻域内无界。 -
第11题：
单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（ ）。A对任意x，f′（x）＞0
B对任意x，f′（x）≤0
C函数－f（－x）单调增加
D函数f（－x）单调增加
正确答案： A解析：
令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。 -
第12题：
问答题设函数f（x）在（a，b）内连续，a＜x1＜x2＜…＜xn＜b，证明：必∃ξ∈（a，b），使f（ξ）＝[f（x1）＋f（x2）＋…＋f（xn）]/n。正确答案：
设f(x)在[x1,xn]上的最大值为M,最小值为m。
则由题设可知,f(x)在[x1,xn]上连续,则它在[x1,xn]上必有最大值和最小值,则m≤[f(x1)+f(x2)+…+f(xn)]/n≤M。
由最值介值定理可知,必∃ξ∈[x1,xn]⊂(a,b),使得f(ξ)=[f(x1)+f(x2)+…+f(xn)]/n。解析： 暂无解析 -
第13题：
设f（x）在（-∞，+∞）内可导，则下列命题正确的是（ ）
答案：D解析：
-
第14题：
函数f(x)=｜xsinx｜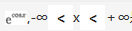
是().
A.有界函数
B.单调函数
C.周期函数
D.偶函数答案：D解析：显然函数为偶函数，选(D). -
第15题：
函数：y=sin1/x在定义域内是：
A.单调函数 B.周期函数
C.无界函数 D.有界函数答案：D解析：提示:利用sin(1/x)的图形或取绝对值 sin(1/x) ≤1确定。 -
第16题：
设函数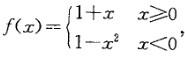
在(-∞，+∞)内：
A.单调减少 B.单调增加
C.有界 D.偶函数答案：B解析：提示:方法一可通过画出的图形判定，方法二求导数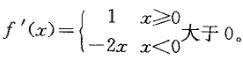
-
第17题：
设{en}是单调增加的有界数列，则下列级数中收敛的是
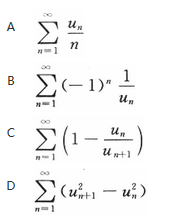答案：D解析：
-
第18题：
设?(x)为开区间(a，b)上的可导函数，则下列命题正确的是（ ）A.(x)在(a，b)上必有最大值
B.(x)在(a，b)上必一致连续
C.(x)在(a，b)上必有界
D.(x)在(a，b)上必连续答案：D解析：根据微积分的知识，可导的函数必连续，
-
第19题：
设函数在（a，b）内连续，则在（a，b）内（）。
- A、f（x）必有界
- B、f（x）必可导
- C、f（x）必存在原函数
- D、D.必存在一点ξ∈（a，，使f（ξ）=0
正确答案:C -
第20题：
下列命题正确的是（）。
- A、分段函数必存在间断点
- B、单调有界函数无第二类间断点
- C、在开区间连续，则在该区间必取得最大值和最小值
- D、在闭区间上有间断点的函数一定有界
正确答案:B -
第21题：
单选题下列说法正确的是（ ）。A单调数列必收敛
B收敛数列必单调
C有界数列必收敛
D收敛数列必有界
正确答案： A解析： -
第22题：
单选题f（x）＝|xsinx|ecosx（－∞＜x＜＋∞）是（ ）。A有界函数
B单调函数
C周期函数
D偶函数
正确答案： D解析：
因f（－x）＝|（－x）sin（－x）|ecos（－x）＝f（x），故f（x）为偶函数。 -
第23题：
单选题设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（ ）。A曲线是向上凹的
B曲线是向上凸的
C单调减少
D单调增加
正确答案： C解析：
判断函数的单调性及凹凸性，需求出其导函数和二阶导数，并判断其正负号。g′（x）＝[xf′（x）－f（x）]/x2，构造函数F（x）＝xf′（x）－f（x），F′（x）＝xf″（x）＜0（题中已给出f″（x）＜0），故F（x）单调减少。则F（x）＜F（1）＝0，故g′（x）＜0，即g（x）在（1，＋∞）内单调减少。 -
第24题：
单选题设函数f（x）在（－∞，＋∞）内单调有界，{xn}为数列，下列命题正确的是（ ）。A若{xn}收敛，则{f（xn）}收敛
B若{xn}单调，则{f（xn）}收敛
C若{f（xn）}收敛，则{xn}收敛
D若{f（xn）}单调，则{xn}收敛
正确答案： A解析：
由题意知，若{xn}单调，则{f（xn）}单调有界，则{f（xn）}一定存在极限，即{f（xn）}收敛。