A. xf'(x)-f'(x)+c B.xf'(x)-f(x)+c C.xf'(x)+f'(x)+c D.xf'(x)-f(x)+c
题目
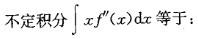
A. xf'(x)-f'(x)+c
B.xf'(x)-f(x)+c
C.xf'(x)+f'(x)+c
D.xf'(x)-f(x)+c
B.xf'(x)-f(x)+c
C.xf'(x)+f'(x)+c
D.xf'(x)-f(x)+c
相似考题
更多“A. xf'(x)-f'(x)+c B.xf'(x)-f(x)+c C.xf'(x)+f'(x)+c D.xf'(x)-f(x)+c”相关问题
-
第1题:
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。A. [f(x)/g(x)]>[f(a)/g(b)]
B. [f(x)/g(x)]>[f(b)/g(b)]
C. f(x)g(x)>f(a)g(a)
D. f(x)g(x)>f(b)g(b)答案:C解析:因为[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)>0,所以函数f(x)g(x)在[a,b]上单调递增。所以,当x∈(a,b)时,f(a)g(a)<f(x)g(x)<f(b)g(b)。 -
第2题:
不定积分∫xf"(x)dx等于:A.xf'(x)-f'(x)+c
B.xf'(x)-f(x)+c
C.xf'(x)+f'(x)+c
D.xf'(x)+f(x)+c答案:B解析: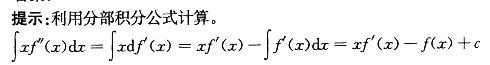
-
第3题:
 A.f(-x,y)=f(x,y),f(x,-y)=-f(x,y)
A.f(-x,y)=f(x,y),f(x,-y)=-f(x,y)
B.f(-x,y)=f(x,y),f(x,-y)=f(x,y)
C.f(-x,y)=-f(x,y),f(x,-y)=-f(x,y)
D.f(-x,y)=-f(x,y),f(x,-y)=f(x,y)答案:B解析:要求f(x,y)关于x和y都是偶函数。 -
第4题:
不定积分∫xf(x)dx等于( )。
A. xf(x)-f(x) + C B. xf(x)-f(x) + C
C. xf(x) + f(x) + C D. xf(x) +f(x)+ C答案:B解析:提示:用分部积分法。 -
第5题:
设函数f(x),g(x)是大于零的可导函数,且f′(x)g(x)-f(x)g′(x)<0,则当a<x<b时有( )《》( )A.f(x)g(b)>f(b)g(x)
B.f(x)g(a)>f(a)g(x)
C.f(x)g(x)>f(b)g(b)
D.f(x)g(x)>f(a)g(a)答案:A解析: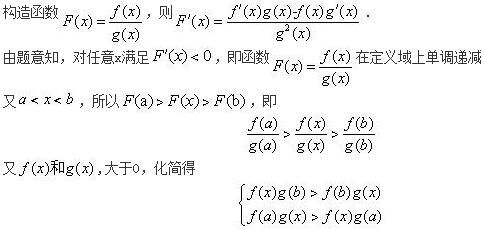
-
第6题:
若f(x)、F(x)分别为随机变量X的密度函数、分布函数,则( )。A.F(x)=f(x)
B.F(x)≥f(x)
C.F(x)≤f(x)
D.f(x)=-F'(x)答案:D解析:
-
第7题:
设F(x)是f(x)的一个原函数,则∫e-xf(e-x)dx等于下列哪一个函数?()
- A、F(e-x)+c
- B、-F(e-x)+c
- C、F(ex)+c
- D、-F(ex)+c
正确答案:B -
第8题:
若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()
- A、(f″(x)f(x)-[f′(x)]2)/[f(x)]2
- B、f″(x)/f′(x)
- C、(f″(x)f(x)+[f′(x)]2)/[f(x)]2
- D、ln″[f(x)]·f″(x)
正确答案:A -
第9题:
设z=f(x2+y2),其中f具有二阶导数,则等于().
- A、2f’(x2+y2)
- B、4x2f"(x2+y2)
- C、2’(x2+y2)+4x2f"(x2+y2)
- D、2xf"(x2+y2)
正确答案:C -
第10题:
单选题设f(u,v)是二元可微函数,z=f(y/x,x/y),则x∂z/∂x-y∂z/∂y=( )。A-yf1′/x+xf2′/y
B2(-yf1′/x+xf2′/y)
C-yf1′/x+2xf2′/y
D-yf1′/x+f2′/y
正确答案: A解析:
设f1′为函数f(u,v)对第一中间变量的偏导,f2′为函数f(u,v)对第二中间变量的偏导,则∂z/∂x=f1′·(-y/x2)+f2′·(1/y),∂z/∂y=f1′·(1/x)+f2′·(-x/y2),x∂z/∂x-y∂z/∂y=2(-yf1′/x+xf2′/y)。 -
第11题:
单选题设y=f(lnx)ef(x),其中f可微,则dy=( )。A[f(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
B[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx
C[f′(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
D[f(lnx)ef(x)/x+f(x)f(lnx)ef(x)]dx
正确答案: A解析:
由y′=f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x),得dy=[f′(lnx)ef(x)/x+f′(x)f(lnx)ef(x)]dx。 -
第12题:
单选题若f″(x)存在,则函数y=ln[f(x)]的二阶导数为:()A(f″(x)f(x)-[f′(x)]2)/[f(x)]2
Bf″(x)/f′(x)
C(f″(x)f(x)+[f′(x)]2)/[f(x)]2
Dln″[f(x)]·f″(x)
正确答案: B解析: 暂无解析 -
第13题:
若∫f(x)dx=F(x)+C,则∫xf(1-x^2)dx=( )。A. F(1-x^2)+C
B. -(1/2)F(1-x^2)+C
C. (1/2)F(1-x^2)+C
D. -(1/2)F(x)+C答案:B解析:∫xf(1-x^2)dx=(-1/2)∫f(1-x^2)d(1-x^2)=(-1/2)F(1-x^2)+C
这里C均表示常数。 -
第14题:
若f(-x)=f(x),且在(0,+∞)内f′(x)>0,f″(x)<0,则f(x)在(-∞,0)内( )。《》( )A.f′(x)<0,f″(x)<0
B.f′(x)<0,f″(x)>0
C.f′(x)>0,f″(x)<0
D.f′(x)>0,f″(x)>0答案:A解析:已知在给出的(0,+∞)内,f′(x)>0,f″(x)<0,故在(0,+∞)上f(x)单调递增,且图形是凸的,再根据已知条件f(-x)=f(x)可知f(x)是偶函数,利用图形的对称性可得出f(x)在(-∞,0)是单调递减且也是凸的。故应该选择A。 -
第15题:
设,在x=0连续,且对任何x,y∈R有f(x﹢y)=f(x)﹢f(y)
证明:(1)f在R上连续;(2)f(x)=xf(1)。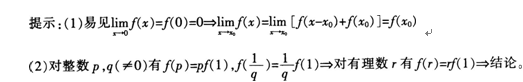 答案:解析:(1)因f(0) =f(0+0)=f(0) +f(0) =2f(0),所以f(0)=0。又对任意算∈(一∞,+∞)有△y=f(x+△x) -f(x) =f(x) +f(△x) -f(x) =f(△x)
答案:解析:(1)因f(0) =f(0+0)=f(0) +f(0) =2f(0),所以f(0)=0。又对任意算∈(一∞,+∞)有△y=f(x+△x) -f(x) =f(x) +f(△x) -f(x) =f(△x)
(2)先证对任意有理数r,都有以rx)=rf(x)。事实上,令y=x,得以2x)=2f(x),由数学归纳法
-
第16题:
设f(x)为连续函数,那么 等于( )。
等于( )。
A. f(x + b) + f(x+a) B. f(x + b)-f(x + a) C. f(x+b)-f(a) D. f(b)-f(x+a)答案:B解析: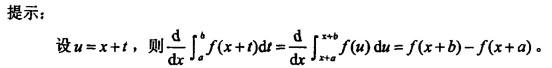
-
第17题:
若f(x)=-f(-x),在(0,+∞)内f′(x)>0,f″(x)>0,则在(-∞,0)内( )《》( )A.f′(x)<f″(x)<0
B.f′(x)<f″(x)>0
C.f′(x)>f″(x)<0
D.f′(x)>f″(x)>0答案:C解析:
-
第18题:
烤烟XF各等级代号为X1F、X2F、()。
X3F、X4F
略 -
第19题:
不定积分∫xf″(x)dx等于:()
- A、xf′(x)-f′(x)+c
- B、xf′(x)-f(x)+c
- C、xf′(x)+f′(x)+c
- D、xf′(x)+f(x)+c
正确答案:B -
第20题:
X→Y∈F+()
- A、X∈XF+
- B、X∈YF+
- C、Y∈YF+
- D、Y∈XF+
正确答案:D -
第21题:
单选题不定积分∫xf″(x)dx等于:()Axf′(x)-f′(x)+c
Bxf′(x)-f(x)+c
Cxf′(x)+f′(x)+c
Dxf′(x)+f(x)+c
正确答案: B解析: 暂无解析 -
第22题:
单选题∫xf″(x)dx=( )。Axf′(x)-∫f(x)dx
Bxf′(x)-f′(x)+C
Cxf′(x)-f(x)+C
Df(x)-xf′(x)+C
正确答案: B解析:
∫xf″(x)dx=∫xd[f′(x)]=xf′(x)-∫f′(x)dx=xf′(x)-f(x)+C。 -
第23题:
单选题若∫f(x)dx=F(x)+C,则∫xf(1-x2)dx=( )。[2018年真题]AF(1-x2)+C
B(-1/2)F(1-x2)+C
C(1/2)F(1-x2)+C
D(-1/2)F(x)+C
正确答案: B解析:
计算得∫xf(1-x2)dx=(-1/2)∫f(1-x2)d(1-x2)=(-1/2)F(1-x2)+C,这里C均表示常数。
