美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?
题目
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?
相似考题
参考答案和解析
答案:
解析:
相对于无补贴,波音公司的利润增加了36 -16 =20,空客公司的利润减少了16-9=7。美国 政府补贴额为3q1=18,美国作为整体,利润增加了20 - 18=2。
更多“ 美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?”相关问题
-
第1题:
某国电信市场原本由一家公司经营,其成本函数为TC=Q2- 10Q +30,市场需求为Qd=15 -P (1)求市场均衡产量、均衡价格及利润。 (2)现将该公司拆分为A、B两家公司,由于技术水平和规模状态的不同,A、B两家公司的成本,函数分别为
(A)假设两家公司独立行动,各自谋求本公司利润最大化,求均衡时A、B两家公司的产量、利润和市场价格。 (B)若两家公司共谋形成卡特尔,求均衡时A、日两家公司的产量、利润和市场价格。答案:解析:
-
第2题:
假定某寡头厂商面临一条弯折的需求曲线,产量在0~30单位范围内时需求函数为P=60-0.3Q,产量超过30单位时需求函数为P=66 -0.50;该厂商的短期总成本函数为STC=0.005 Q3-0. 2Q2 +36Q +200。 (1)求该寡头厂商利润最大化的均衡产量和均衡价格。 (2)假定该厂商成本增加,导致短期总成本函数变为STC =0.005Q3 -0.2Q2 +50Q +200,求该寡头厂商利润最大化的均衡产量和均衡价格。 (3)对以上(1)和(2)的结果作出解释。
答案:解析:
边际成本函数为MC=0.015Q2 -0.4Q+36。 在Q =30时,边际收益的上限和下限分别为42、36。故在产量为30单位时,边际收益曲线间断部分的范围为36—42。 由厂商的边际成本函数可知,当Q =30时,有MC=37.5。 根据厂商的最大化利润原则,由于MC= 37.5处于边际收益曲线间断部分的范围MR=MC为36—42之内,符合利润最大化原则,所以厂商的产量和价格分别为Q=30、P=51。 (2)厂商边际成本函数为MC =0.015Q2-0. 4Q +50。 当Q =30时,MC= 51.5。 超出了边际收益曲线间断部分的范围36~ 42,此时根据厂商利润最大化原则MR= MC,得Q =20,P=54。 (3)由(1)结果可知,只要在Q=30时MC值处于边际收益曲线间断部分36—42范围之内,寡头厂商的产量和价格总是为Q= 30、P=51,这就是弯折曲线模型所解释的寡头市场的价格刚性现象。 只有边际成本超出了边际收益曲线间断部分36—42的范围,寡头市场的均衡价格和均衡产量才会发生变化。 -
第3题:
假定某寡头市场有两个厂商生产同种产品,市场的反需求函数为P=100—Q,两个厂商的成本函数分别为TC1=20Q,TC2=0.5Q22。 (1)假定两厂商按古诺模型行动,求两厂商各自的产量和利润量,以及行业的总利润量。 (2)假定两厂商联合行动组成卡特尔,追求共同利润最大化,求两厂商各自的产量和利润量,以及行业的总利润量。 (3)比较(1)与(2)的结果。答案:解析:(1)对于第一个厂商而言: π1= PQ1 - TC1
-
第4题:
假设某大宗商品的国际需求函数Q=a-P。两个寡头公司1和2向该市场提供同质产品,拥有不变的单位边际成本,分别为c1和c2,且有a>c2 >c1。若两个企业的供给能力充足而展开伯川德(Bertrand)竞争,则各自的纳什均衡价格策略是什么?答案:解析:伯川德的均衡情况为:对于厂商1来说,其利润函数为:π1(q1,q2)=(P-c)·D1 (q1,q2),这里 D1 (q1,q2)表示厂商1的需求函数,由下式给出:
从上式可知,如果厂商1的定价Pl大于厂商2的定价P2,则厂商1会失去整个市场,对其产品的 需求为零,该厂商的利润也就为零;但如果P1C2>C1,厂商1肯定会以P2=C2 -ε(ε>0,且是个无穷小量)的价格进行生产,此时 厂商1会占领所有的市场份额,厂商2停产。 -
第5题:
一个垄断厂商生产某种产品的成本函数为:C=5+3Q,将其产品在两个地理分割的市场上销售,这两个市场对该产品的需求函数分别为:P1=15-Q1,P2=25-2Q2。 假设企业被禁止使用价格歧视策略,那么该企业将采取何种价格策略?能够在两个市场各自销售多少产品?两个市场总共实现多少利润?在两个市场上分别造成多少福利损失?答案:解析:
-
第6题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。问这两个公司是否愿意合谋而平分垄断利润?答案:解析:两个公司愿意合谋并平分利润。 合并后的总利润函数为: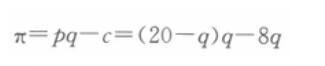
利润最大化的一阶条件为:
解得:q=6,p=14,π=36。 若两个公司平分利润,有π1=π2=18>16,所以两个公司愿意合谋而平分垄断利润。 -
第7题:
某小镇的电影公司的市场需求函数是Q=500-20P,这里P是每场电影的票价,Q是观看电影的需求;公司播放电影的成本函数C(Q) =100+0. 5Q。 (1)电影公司的每场票价定在多少合适? (2)电影公司决定对长者进行票价优惠,经市场调查发现,65岁以上长者的需求是Q1=50-20P。电影公司决定对长者凭证购票优惠,公司应该如何实行对长者优惠票价? (3)电影公司是否同时需要调整非长者票价?答案:解析:(1)由已知可得市场反需求函数为:P=25- Q,则电影公司的利润函数为: π=PQ-C= (25-- Q) Q- (100+0. 5Q) =24. 5Q- Q2-100 利润最大化的一阶条件为: =24.5-0.1Q=0,可得:Q= 245。且满足利润最大化的二阶条件: =-0.1<0。因此,电影公司应将每场票价定为:P=25- Q=12. 75。 (2)由于长者的需求为Q1=50-20P,电影公司实现利润最大化要求MR1=MC,即有: 2.5- (1/10)Q1 =0.5 解得:Q1 =20,此时对长者优惠票价为:P1=2.5- Q1 =1.5。 (3)电影公司需要同时调整非长者票价。若长者的均衡需求为20,总需求245不变,则非长者的需求为Q2=Q-Q1=225,则P=25- Q=13. 75, -
第8题:
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果政府规定,禁止在不同市场上制定不同的价格,求此时该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。答案:解析:
-
第9题:
已知某完全垄断企业的需求函数为P=17-4Q,成本函数为TC=5Q+2Q2。 (1)计算企业利润最大化的价格和产出、利润。 (2)如果政府实行价格管制,按边际成本定价与按平均成本定价,价格分别是多少?厂商是否亏损?
(1)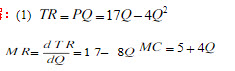 当MR=MC 时获得最大利润 即 17-8=5+4Q
当MR=MC 时获得最大利润 即 17-8=5+4Q
所以Q=1; P=13 π=TR-TC=PQ-TC=13×1-(5×1+2×12)=6
(2) MC==5+4Q AC=5+2Q 当P=AC 17-40=5+2Q Q=2 P=5+2Q=4+4=9
则:TC=10+8=18 TR=PQ=9×2=18 所以盈亏持平。
当P=MC 17-4Q=5+4Q Q=1.5 P=5+4Q=11 TC=5Q+2Q2=7.5+4.5=12
TR=PQ=11×1.5=16.5 所以盈利。
略 -
第10题:
某寡头垄断市场上有两个厂商,总成本均为自身产量的20倍, 市场需求函数为Q=200-P。若两个厂商达成协议垄断市场,共同安排产量,则各自的利润情况如何?
正确答案:200-2Q=20,Q=90,Q1=Q2=45 -
第11题:
问答题某生产商通过统计分析得:需求函数:Q=1000—4p成本函数:C=6000+50Q如果公司以利润最大化为定价目标,则其价格为多少的时候可取得最大利润?最大利润是多少?(提示:依据成本、收入和利润之间的关系,设立公式)正确答案: 设:利润为Z,销售收入为R
则:Z=R–C
=PQ–C
∵Q=1000-4PC=6OOO+5Q
=P(1000-4P)-(6000+50Q)
=-56000+1200P-4P2
根据二次函数求极值原理,欲使Z最大,则:
P=1200/2×(4)=150
那么,最大利润maxZ=56000+1200–4×1502
=34000解析: 暂无解析 -
第12题:
问答题假设垄断企业的成本函数为50+20Q,其面对的市场需求函数为P=100-4Q,试求垄断企业利润最大化的产量、价格与利润。正确答案:
垄断企业其面对的市场需求函数为P=100—4Q,边际收益为:MR=100-8Q;
边际成本为:MC=20;
由MR=MC可以解得:Q=10;
价格为:P=100-4Q=60;
利润为:10×60-50-20×10=350。解析: 暂无解析 -
第13题:
假设某大宗商品的国际需求函数Q=a-P。两个寡头公司1和2向该市场提供同质产品,拥有不变的单位边际成本,分别为c1和c2,且有a>c2 >c1。 若两个公司展开古诺(Cournot)竞争,则各自的纳什均衡产量q1和q2是多少?答案:解析:若两个企业展开古诺竞争,则寡头公司1的利润函数为: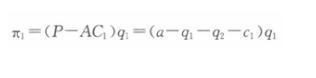
利润最大化的一阶条件为: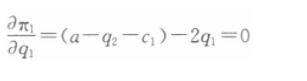
从而寡头公司1的反应函数为: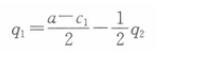
寡头公司2的利润函数为: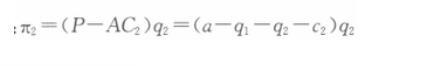
同理可得其反应函数为: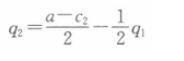
联立两个公司的反应函数①②可得: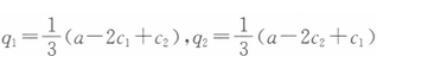
此即为古诺竞争 下的纳什均衡产量。 -
第14题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。 假定两公司都生产,找出古诺/纳什均衡并求出均衡时的产量、价格与利润。答案:解析:在寡头市场上,生产的古诺均衡解是假定一方产量不变,另一方实现自身利润最大化的解,因此也是纳什均衡解。 波音公司的利润函数为: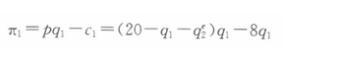
利润最大化的一阶条件为: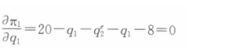
由此得波音公司的反应函数为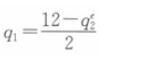
同理可得,空客公司的反应函数为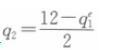
令q1 =qe1,q2=qe2,联立两个反应函数,得到古诺均衡解为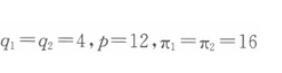
-
第15题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。上问中的结果反映古诺模型假定是否合适?为什么?答案:解析:上述结果反映古诺模型假定合适。古诺均衡解是纳什均衡解,在均衡状态,假定一方的产量不变,另一方为实现利润最大化的产量也不会发生变化。若某一方的产量偏离了均衡状态,双方的利润均会减少,且主动改变产量的一方利润减少更多。在(4)的结果中,美国政府对波音公司进行补贴,从而改变了波音公司的成本函数。在新的古诺均衡中,波音公司的产量增加,而美国作为整体的利润却变为2,小于补贴前的16;同时,空客公司的利润变为9,也小于之前的16,但利润下降幅度比美国少。 -
第16题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。假定美国政府决定给予波音公司每架飞机3单位的生产补贴,问新的古诺/纳什均衡(价格、产量与各自利润)为多少?答案:解析:美国政府给予波音公司补助后,波音公司的成本函数变为c’1(q1)=8q1-3q1=5q1,波音公司 的利润函数变为:
利润最大化的一阶条件为:
得波音公司的反应函数为
同理可得空客公司的反应函数为
令q1=qe1,q2一qe2,联立两个反应函数,得到古诺均衡解为:q1 =6,q2 =3;p=11;π1=36,π2 =9。 -
第17题:
竞争性市场下有3个完全相同的企业,生产相同产品。市场的反需求曲线为p(Q)-l-Q,Q=q1+q2+q3,每个企业成本为零。若其中两个公司合并,企业各自的利润分别是多少?答案:解析:不妨设企业1和2合并为企业4,那么企业4的利润函数为π4=p4q4=(1- q3 - q4)q4,利润最大化的一阶条件为: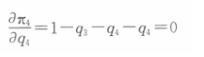
得厂商4的反应函数为
同理可得厂商3的反应函数为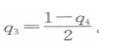
联立两个反应函数,得到古诺均衡解为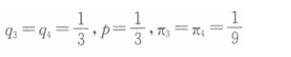
若企业1和2平分利润,则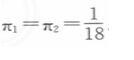
-
第18题:
假设某完全竞争行业有200个相同的企业,企业的短期成本函数为TC =0. 2Q2+Q+15,市场需求函数为Qp= 2475 - 95P,厂商的长期总成本函数为LTC=0.1Q3-1. 2Q2+11.1Q,求: (1)市场短期均衡价格、产量及厂商利润。 (2)市场长期均衡价格与产量。 (3)说明是否会有厂商退出经营。答案:解析:(1)先求单个企业的供给函数: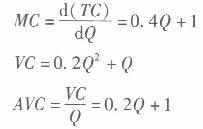
故A VC的最小值为1。 而MC的最小值也为1,故只有价格大于等于1,厂商才会供给商品。 此时单个企业的供给函数为P= MC =0.4Q +l,即Q=2.SP -2.5。 市场的供给函数为Qs=200Q =500P -500(P≥1),由QD=QS可得P=5。 市场均衡产量为2000单位,每个厂商产量为10单位。 单个厂商利润为5 x10 - (0.2 x102 +10+15) =5。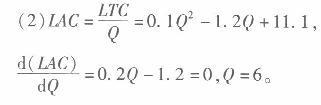
将Q=6代入LAC,得IAC =7.5。 由长期均衡条件可得P=7. 5. (3)将P=7.5代入需求函数可得市场需求量为1762.5,而200个厂商的供给量为1200,再加上厂商短期利润为正,长期利润为O,所以没有厂商退出经营。 -
第19题:
美国的波音公司与法国的空客公司都向世界出售民用客机。假设世界对飞机的需求函数为p=20-q,两个公司的成本函数均为c(q)=8q。(1)相对于无补贴的均衡,两个公司各自的利润是否改变?美国政府作为整体,利润是否改变?
上问中的结果反映古诺模型假定是否合适?为什么?答案:解析:相对于无补贴,波音公司的利润增加了36 -16 =20,空客公司的利润减少了16-9=7。美国 政府补贴额为3q1=18,美国作为整体,利润增加了20 - 18=2。
上述结果反映古诺模型假定合适。古诺均衡解是纳什均衡解,在均衡状态,假定一方的产量不变,另一方为实现利润最大化的产量也不会发生变化。若某一方的产量偏离了均衡状态,双方的利润均会减少,且主动改变产量的一方利润减少更多。在(1)的结果中,美国政府对波音公司进行补贴,从而改变了波音公司的成本函数。在新的古诺均衡中,波音公司的产量增加,而美国作为整体的利润却变为2,小于补贴前的16;同时,空客公司的利润变为9,也小于之前的16,但利润下降幅度比美国少。 -
第20题:
一厂商分别向东西部两个市场销售Q1与Q2单位的产品。已知厂商的总成本函数为C=5+3(Q1+Q2),东部市场对该产品的需求函数为P1=15-Q1,西部市场对该产品的需求函数为P2=25一2Q2。 如果该厂商可以将东西部市场区分开,在不同的市场制定不同的价格出售,求该厂商利润最大化时的P1、P2、Q1、Q2以及边际收益、总利润。答案:解析:
-
第21题:
()是全球航空航天业的领袖公司,也是世界上最的民用和军用飞机制造商
- A、空客公司
- B、麦道公司
- C、中国民用航空
- D、波音公司
正确答案:D -
第22题:
问答题假设某垄断竞争厂商的产品需求函数为P=9400-4Q,成本函数为TC=4000+3000Q,求该厂商均衡时的产量、价格和利润。正确答案: 根据利润最大化原则MR=MC,MR=9400-8Q,MC=3000,得Q=800,P=6200,π=TR-TC=2556000解析: 暂无解析 -
第23题:
问答题某垄断者的产品在两个分割市场出售,产品的成本函数和两个市场的需求函数分别为TC=Q2+10Q,Q1=32-0.4P1,Q2=18-0.1P2,其中Q=Q1+Q2。 (1)假设两个市场能实行差别价格,求解利润最大时的两个市场的售价、销售量和利润。 (2)假设两个市场只能索取相同价格,求解利润最大时的售价、销售量和利润。正确答案: (1)由成本函数可得出边际成本为:MC=TC′=2(Q1+Q2)+10。
由需求函数可得出反需求函数分别为:
P1=80-2.5Q1,P2=180-10Q2
TR1=P1Q1=(80-2.5Q1)Q1,可得出:MR1=80-5Q1;
TR2=P2Q2=(180-10Q2)Q2,可得出:MR2=180-20Q2。
根据三级价格歧视利润最大化均衡条件MR1=MR2=MC,即有:
80-5Q1=180-20Q2=2(Q1+Q2)+10
解得:Q1=8,Q2=7,Q=15。
将销售量分别代入各自的反需求函数,可得:P1=60,P2=110。
厂商利润:π=P1Q1+P2Q2-TC=60×8+110×7-152-10×15=875。
(2)若两个市场只能卖同一价格,即P1=P2,则:
Q=Q1+Q2=32-0.4P+18-0.1P=50-0.5P
由需求函数可得出反需求函数为:P=100-2Q。
TR=PQ=(100-2Q)Q,可得出:MR=100-4Q。
根据利润最大化均衡条件MR=MC,解得:Q=15。
将销售量代入反需求函数,可得:P=70。
在这一价格下,Q1=4,Q2=11,说明当P=70时厂商在两个市场上都售出了产品。
厂商利润π=PQ-TC=70×15-152-10×15=675。解析: 暂无解析

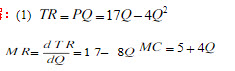 当MR=MC 时获得最大利润 即 17-8=5+4Q
当MR=MC 时获得最大利润 即 17-8=5+4Q