微分方程的通解为
题目
微分方程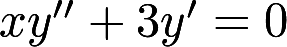 的通解为
的通解为
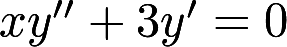 的通解为
的通解为相似考题
更多“微分方程的通解为”相关问题
-
第1题:
微分方程(3+2y)xdx+(1+x2)dy=0 的通解为: 答案:B解析:
答案:B解析:
-
第2题:
微分方程y''+2y=0的通解是:
(A,B为任意常数)答案:D解析:提示:本题为二次常系数线性齐次方程求通解,写出方程对应的特征方程r2+2 = 0,r =
-
第3题:
微分方程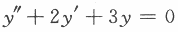 的通解为y=________.答案:解析:
的通解为y=________.答案:解析:
-
第4题:
微分方程yy'=1的通解为()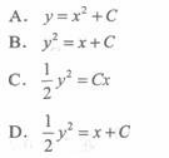 答案:D解析:
答案:D解析: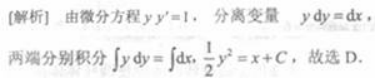
-
第5题:
微分方程y''+y=0的通解是 .答案:解析:【考情点拨】本题考查了二阶线性微分方程的通解知识点.【应试指导】微分方程y''+y=0的特征方程是r2+1=0. -
第6题:
系统微分方程的通解
正确答案: 系统由于初始条件引起的瞬态响应过程。 -
第7题:
填空题微分方程y″-2y′+2y=ex的通解为____。正确答案: y=ex(c1cosx+c2sinx)+ex解析:
原微分方程为y″-2y′+2y=ex,其对应的齐次方程为y″-2y′+2y=0,该齐次方程的特征方程为r2-2r+2=0,解得r1,2=1±i。故原方程对应的齐次方程的通解为y=ex(c1cosx+c2sinx)。设y*=Aex为原方程的特解,将其代入原方程可解得A=1。故原方程的通解为y=ex(c1cosx+c2sinx)+ex。 -
第8题:
填空题微分方程xy″+3y′=0的通解为____。正确答案: y=-c1/(2x2)+c2解析:
原微分方程为xy″+3y′=0,令y′=p,则y″=p′,则原方程变形为xp′=-3p,即dp/dx=-3p/x,分离变量并两边积分得∫(dp/p)=-∫(3/x)dx,ln|p|=-3ln|x|+ln|c|,p=c1x-3,即y′=c1/x3。故y=-c1/(2x2)+c2,此即为原微分方程的通解。 -
第9题:
微分方程y′′=x+sinx的通解是(C1,C2为任意常数): 答案:B解析:
答案:B解析:
-
第10题:
微分方程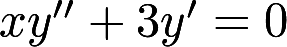 的通解为答案:解析:
的通解为答案:解析: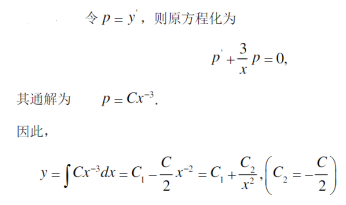
-
第11题:
微分方程(1+2y)xdx+(1+x2)dy的通解为:(c为任意常数) 答案:B解析:提示 方程为一阶可分离变量方程,分离变量后求解。
答案:B解析:提示 方程为一阶可分离变量方程,分离变量后求解。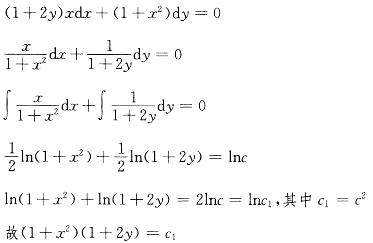
-
第12题:
以. 为通解的二阶线性常系数齐次微分方程为_____答案:解析:所给问题为求解微分方程的反问题.常见的求解方法有两种:解法1先由通解写出二阶线性常系数齐次微分方程的特解,再由此写出方程的特征根r1,
为通解的二阶线性常系数齐次微分方程为_____答案:解析:所给问题为求解微分方程的反问题.常见的求解方法有两种:解法1先由通解写出二阶线性常系数齐次微分方程的特解,再由此写出方程的特征根r1,
r2,第三步写出特征方程(r-r1)(r-r2)=0,再依此写出相应的微分方程;
解法2由所给方程的通解,利用微分法消去任意常数,得出微分方程.这里只利用解法1求解.由于二阶线性常系数齐次微分方程的通解为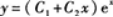 ,由其解的结构定理可知方程有两个特解:
,由其解的结构定理可知方程有两个特解: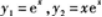 ,从而知道特征方程的二重根r=1.
,从而知道特征方程的二重根r=1.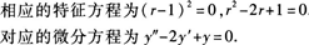
-
第13题:
微分方程的含有任意常数的解是该微分方程的通解。
正确答案:正确 -
第14题:
函数是微分方程的()。
- A、通解
- B、特解
- C、是解,但既非通解也非特解
- D、不是解
正确答案:B -
第15题:
名词解释题系统微分方程的通解正确答案: 系统由于初始条件引起的瞬态响应过程。解析: 暂无解析
