微分方程xdy-ydx=2dy的通解为____________________.

题目

微分方程xdy-ydx=2dy的通解为____________________.

相似考题

1.微分方程y′-3y =O的通解为______.

2.微分方程（3+2y）xdx+（1+x2）dy=0 的通解为:

3.微分方程的通解为

4.微分方程的通解为y=________.

参考答案和解析
正确答案：
更多“微分方程xdy-ydx=2dy的通解为____________________.”相关问题

  • 第1题：

    3阶常系数线性齐次微分方程的通解为y=________


    答案：
    解析：

  • 第2题：

    微分方程y''=x+sinx的通解是（c1，c2为任意常数）：


    答案：B
    解析：
    提示 本题为可降阶的高阶微分方程，连续积分二次，得通解。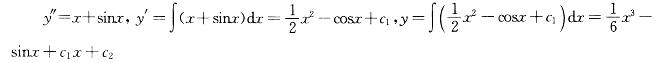

  • 第3题：

    微分方程(1+2y)xdx+(1+x2)dy的通解为:（c为任意常数）


    答案：B
    解析：
    提示 方程为一阶可分离变量方程，分离变量后求解。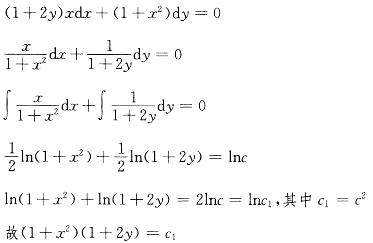

  • 第4题：

    下列解中是某二阶常微分方程的通解为《》（ ）



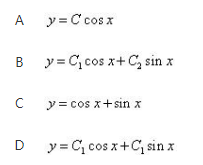    答案：B
    解析：

  • 第5题：

    以.为通解的二阶线性常系数齐次微分方程为_____


    答案：
    解析：
    所给问题为求解微分方程的反问题．常见的求解方法有两种：解法1先由通解写出二阶线性常系数齐次微分方程的特解，再由此写出方程的特征根r1，
    r2，第三步写出特征方程(r-r1)(r-r2)=0，再依此写出相应的微分方程；
    解法2由所给方程的通解，利用微分法消去任意常数，得出微分方程．这里只利用解法1求解．由于二阶线性常系数齐次微分方程的通解为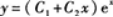，由其解的结构定理可知方程有两个特解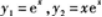：，从而知道特征方程的二重根r=1．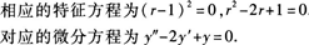

  • 第6题：

    微分方程dy+xdx=0的通解y=_____.


    答案：
    解析：
    【解析】所给方程为可分离变量方程．

  • 第7题：

    微分方程的含有任意常数的解是该微分方程的通解。


    正确答案:正确

  • 第8题：

    单选题
    微分方程xdy－ydx＝y2eydy的通解为（　　）。
    A

    y＝x（ex＋C）

    B

    x＝y（ey＋C）

    C

    y＝x（C－ex）

    D

    x＝y（C－ey）


    正确答案： C
    解析：
    原微分方程xdy－ydx＝y2eydy，变形可得（xdy－ydx）/y2＝eydy，即－d（x/y）＝d（ey），积分得－x/y＝ey－C。即x＝y（C－ey）就是微分方程的通解。

  • 第9题：

    微分方程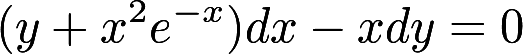的通解是=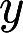


    答案：
    解析：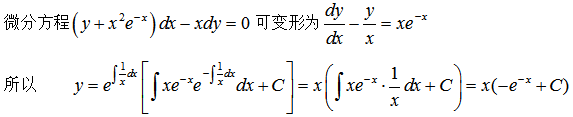

  • 第10题：

    微分方程xy'-ylny=0的通解为( )。

    A、y=cex
    B、y=clnx
    C、y=lncx
    D、y=ecx

    答案：D
    解析：
    方程是可分离变量的方程，可化为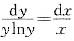，两边积分得lnlny=lnx+lnc，即其通为y=ecx

  • 第11题：

    微分方程y′+y=0的通解为（ ）.《》（ ）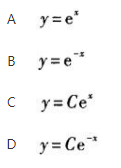


    答案：D
    解析：

  • 第12题：

    微分方程yy'=1的通解为（）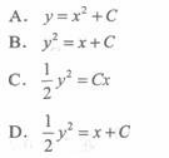


    答案：D
    解析：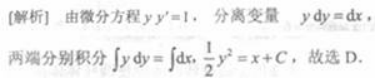

  • 第13题：

    微分方程y''+y=0的通解是 .


    答案：
    解析：
    【考情点拨】本题考查了二阶线性微分方程的通解知识点.【应试指导】微分方程y''+y=0的特征方程是r2+1=0.

  • 第14题：

    微分方程y′-2xy=0的通解为y=_____.


    答案：
    解析：
    所给方程为可分离变量方程．

  • 第15题：

    单选题
    微分方程2yy″＝（y′）2的通解为（　　）。
    A

    y＝（x－c）2

    B

    y＝c1（x－1）2

    C

    y＝c1＋（x－c）2

    D

    y＝c1（x－c2）2


    正确答案： C
    解析：
    由于二阶微分方程的通解中应该有两个独立的未知常数，故可排除A、B项。将C、D项代入原方程，C项代入后等式两边不相等，故排除C项，D项代入后等式两边相等。

相关内容