设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型（1）求常数a; (2）求可逆线性变换矩阵C

题目
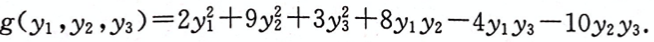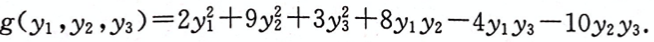设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型（1）求常数a; (2）求可逆线性变换矩阵C

相似考题

1.设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ).A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同

2.设A是3阶矩阵，P=(a1,a2,a3)是3阶可逆矩阵， 若矩阵Q=(a1,a2,a3)，则Q-1AQ=

3.设二次型. （Ⅰ）求二次型的矩阵的所有特征值； （Ⅱ）若二次型的规范形为，求的值

4.A.|A|＞0 B. C.f的正惯性指数p=n D.f的负惯性指数q=0

更多“设二次型的正惯性指数p=2,负惯性指数q=0,且可用可逆线性变换x=Cy将其化为二次型（1）求常数a; (2）求可逆线性变换矩阵C”相关问题

  • 第1题：

    设二次型
    　　(b>0),
    　　其中二次型的矩阵A的特征值之和为1，特征值之积为-12.
    　　(1)求a，b的值；
    　　(2)利用正交变换将二次型f化为标准形，并写出所用的正交变换和对应的正交矩阵.


    答案：
    解析：

  • 第2题：

    设随机变量X,y相互独立,且X～P(1),y～P(2),求P(max{X,Y}≠0)及P(min{X,Y}≠0).


    答案：
    解析：

  • 第3题：

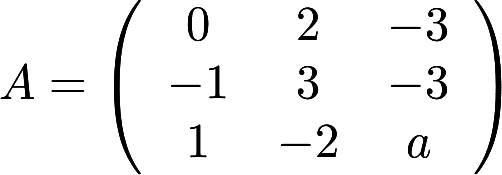    设矩阵相似于矩阵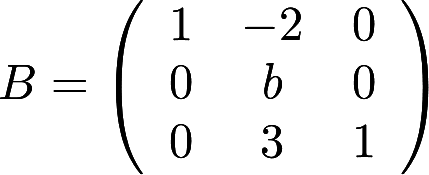. （1）求a,b的值；（2）求可逆矩阵P，使为对角阵


    答案：
    解析：

  • 第4题：

    设连续型随机变量X的分布函数为F(x)=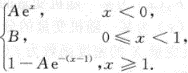
    　　(1)求常数A,B;(2)求X的密度函数f(x)；(3)求P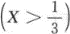


    答案：
    解析：

  • 第5题：

    设n阶矩阵A满足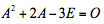，（1）证明A，A+2E，A+4E可逆，并求它们的逆；（2）当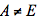时，判断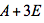是否可逆，并说明理由。


    答案：
    解析：

  • 第6题：

    设二次型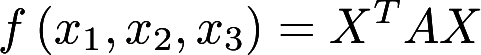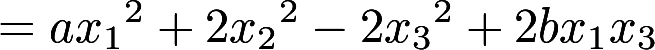,(b>0)其中A的特征值之和为1, 特征值之积为-12.(1) 求a,b. (2) 用正交变换化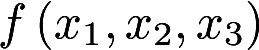为标准型


    答案：
    解析：

  • 第7题：

    设n阶矩阵A可逆，且detA=a，求，.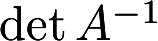


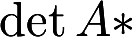    答案：
    解析：

  • 第8题：

    设二次型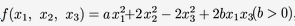其中二次型矩阵A的特征值之和为1, 特征值之积-12.(1) 求a,b的值; (2) 求一正交变换把二次型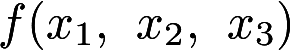化成标准型(需写出正交变换及标准型)


    答案：
    解析：

  • 第9题：

    设矩阵A=
    　　(1)已知A的一个特征值为3，试求y;
    　　(2)求可逆矩阵P，使(AP)^T(AP)为对角矩阵.


    答案：
    解析：

  • 第10题：

    已知a是常数，且矩阵可经初等列变换化为矩阵.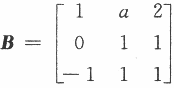
    　　(Ⅰ)求a；
    　　(Ⅱ)求满足AP=B的可逆矩阵P.


    答案：
    解析：

  • 第11题：

    三阶矩阵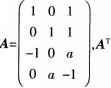 为矩阵A的转置，已知r(ATA)=2，且二次型
    (1)求a；
    (2)求二次型对应的二次矩阵，并将二次型化为标准型，写出正交变换过程。


    答案：
    解析：
    (1)由r(ATA)=r(A)=2可得， (2）

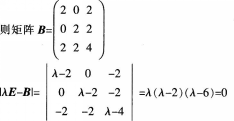
  • 第12题：

    设A是3阶矩阵，P = (α1，α2，α3)是3阶可逆矩阵，且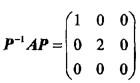，若矩阵Q=(α2，α1，α3),则Q-1AQ=( )。


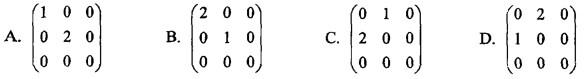    答案：B
    解析：
    提示：由条件知，λ1=1，λ2=2，λ3=0是矩阵A的特征值,而α1，α2，α3是对应的特征向量，故有。

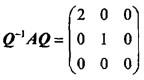  • 第13题：

    已知二次型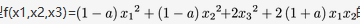的秩为2.(1)求a.(2)求作正交变换X=QY,把f(x1,x2,x3)化为标准形.(3)求方程f(x1,x2,x3)=0的解


    答案：
    解析：

  • 第14题：

    设二次型的正、负惯性指数分别为1，2，则


    A.a大于1
    B.a小于-2
    C.-2
    D.a=1或a=-2


    答案：
    解析：

  • 第15题：

    设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B.
    　　(1)证明B可逆；
    　　(2)求AB^-1.


    答案：
    解析：

  • 第16题：

    设A是n阶可逆方阵，将A的第i行和第j行对换后得到的矩阵记为B， (1)证明B可逆； (2)求.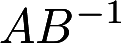


    答案：
    解析：

  • 第17题：

    设U为可逆矩阵, , 证明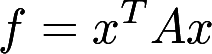为正定二次型


    答案：
    解析：

  • 第18题：

    二次型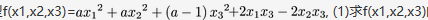, (1)求f(x1,x2,x3)的矩阵的特征值. (2)设f(x1,x2,x3)的规范形为. 求a


    答案：
    解析：

  • 第19题：

    设二次型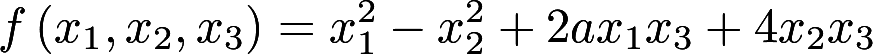的负惯性指数为1，则a的取值范围是


    答案：
    解析：

  • 第20题：

    设二次型f(x1,x2,x3)=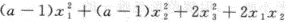（a>0）的秩为2.(1)求a;(2)用正交变换法化二次型为标准形.


    答案：
    解析：

  • 第21题：

    已知矩阵A=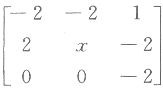与B=相似.
    　　(Ⅰ)求x，y；
    　　(Ⅱ)求可逆矩阵P使得P^-1AP=B.


    答案：
    解析：

  • 第22题：

    设A是3阶矩阵，P=(a1,a2,a3)是3阶可逆矩阵，且P-1AP=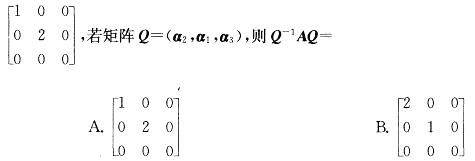


    答案：B
    解析：
    提示 当P-1AP=Λ时，P=(a1,a2,a3)中a1,a2,a3的排列满足对应关系，a1对应λ1，a2对应λ2，a3对应λ3，可知a1对应特征值λ1=1，a2对应特征值λ2=2，a3对应特征值

  • 第23题：

    已知矩阵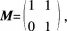求曲线y2=x+y=O在矩阵M-1对应的线性变换作用下得到的曲线方程。


    答案：
    解析：

相关内容