设 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为
题目
设 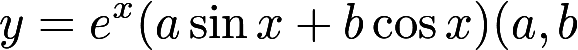 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为
为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为
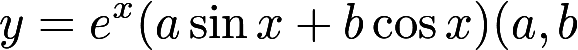 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为
为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为相似考题
更多“设 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为”相关问题
-
第1题:
3阶常系数线性齐次微分方程 的通解为y=________答案:解析:
的通解为y=________答案:解析:
-
第2题:
微分方程(1+2y)xdx+(1+x2)dy的通解为:(c为任意常数) 答案:B解析:提示 方程为一阶可分离变量方程,分离变量后求解。
答案:B解析:提示 方程为一阶可分离变量方程,分离变量后求解。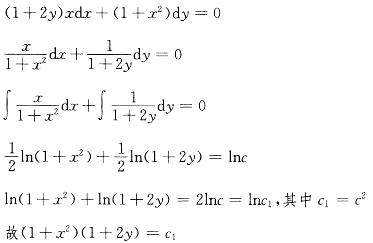
-
第3题:
微分方程y''=y'2的通解是( )(C1、C2为任意常数)。 答案:D解析:提示:这是不显含y可降阶微分方程,令p=y',则dp/dx=y'',用分离变量法求解得,-y'=1/(x+C1) ,两边积分,可得y=C2-ln x+C1 ,故应选D,也可采用检验的方式。
答案:D解析:提示:这是不显含y可降阶微分方程,令p=y',则dp/dx=y'',用分离变量法求解得,-y'=1/(x+C1) ,两边积分,可得y=C2-ln x+C1 ,故应选D,也可采用检验的方式。 -
第4题:
设y1(x)、y2(x)是二阶常系数线性微分方程y″+py′+qy=0的两个线性无关的解,则它的通解为______.答案:解析:由二阶线性常系数微分方程解的结构可知所给方程的通解为 其中C1,C2为任意常数.
其中C1,C2为任意常数. -
第5题:
二阶常系数齐次微分方程y″-4y′+4y=0的通解为_____.答案:解析:
-
第6题:
微分方程的含有任意常数的解是该微分方程的通解。
正确答案:正确 -
第7题:
填空题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=____。正确答案: -xex+x+2解析:
由题意可知,r=1是已知齐次方程对应的特征方程的二重根,则该特征方程为(r-1)2=r2-2r+1=0,齐次方程为y″-2y′+y=0设y*=Ax+B为已知非齐次方程y″-2y′+y=x的特解,代入y″-2y′+y=x得0-2A+Ax+B=x,则A=1,B=2A=2。故已知非齐次方程的通解为y=(C1+C2x)ex+x+2。又y(0)=2,y′(0)=0,代入以上通解得C1=0,C2=-1。故所求方程特解为y=-xex+x+2。 -
第8题:
单选题设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为( )。Ay″-y′+y=0
By″-2y′+2y=0
Cy″-2y′=0
Dy′+2y=0
正确答案: B解析:
根据题中所给的通解y=ex(c1sinx+c2cosx)的结构可知,所求方程对应的特征根为λ1,2=1±i,特征方程为[λ-(1+i)][λ-(1-i)]=λ2-2λ+2=0,则所求方程为y″-2y′+2y=0。 -
第9题:
判断题微分方程的含有任意常数的解是该微分方程的通解。A对
B错
正确答案: 对解析: 暂无解析 -
第10题:
填空题设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为____。正确答案: y″-2y′+2y=0解析:
根据题中所给的通解y=ex(c1sinx+c2cosx)的结构可知,所求方程对应的特征根为λ1,2=1±i,特征方程为[λ-(1+i)][λ-(1-i)]=λ2-2λ+2=0,则所求方程为y″-2y′+2y=0。 -
第11题:
问答题设y1=x,y2=x+e2x,y3=x(1+e2x)是二阶常系数线性非齐次方程的特解,求该方程及其通解。正确答案:
由题意可知,y2-y1=e2x,y3-y1=xe2x是对应齐次方程的两个线性无关的解,齐次方程的通解为y=(C1+C2x)e2x,且特征方程有二重根r1,2=2,则特征方程为(r-2)2=r2-4r+4=0,则齐次方程为y″-4y′+4y=0。
令所求非齐次方程为y″-4y′+4y=f(x),将其解之一y1=x代入得f(x)=4x-4,则所求方程为y″-4y′+4y=4x-4,又齐次方程的通解为y=(C1+C2x)e2x,且非齐次方程的通解为y=(C1+C2x)e2x+x。解析: 暂无解析 -
第12题:
单选题设y=ex(c1sinx+c2cosx)(c1、c2为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为( )。Ay″+2y′+2y=0
By″-2y′+2y=0
Cy″-2y′-2y=0
Dy″+2y′+2y=0
正确答案: A解析:
根据题中所给的通解y=ex(c1sinx+c2cosx)的结构可知,所求方程对应的特征根为λ1,2=1±i,特征方程为[λ-(1+i)][λ-(1-i)]=λ2-2λ+2=0,则所求方程为y″-2y′+2y=0。 -
第13题:
微分方程ydx+(x-y)dy=0的通解是:(c为任意常数) 答案:A解析:
答案:A解析:
-
第14题:
下列解中是某二阶常微分方程的通解为《》( )
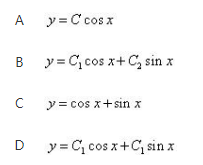 答案:B解析:
答案:B解析: -
第15题:
以. 为通解的二阶线性常系数齐次微分方程为_____答案:解析:所给问题为求解微分方程的反问题.常见的求解方法有两种:解法1先由通解写出二阶线性常系数齐次微分方程的特解,再由此写出方程的特征根r1,
为通解的二阶线性常系数齐次微分方程为_____答案:解析:所给问题为求解微分方程的反问题.常见的求解方法有两种:解法1先由通解写出二阶线性常系数齐次微分方程的特解,再由此写出方程的特征根r1,
r2,第三步写出特征方程(r-r1)(r-r2)=0,再依此写出相应的微分方程;
解法2由所给方程的通解,利用微分法消去任意常数,得出微分方程.这里只利用解法1求解.由于二阶线性常系数齐次微分方程的通解为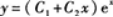 ,由其解的结构定理可知方程有两个特解:
,由其解的结构定理可知方程有两个特解: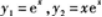 ,从而知道特征方程的二重根r=1.
,从而知道特征方程的二重根r=1.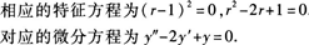
-
第16题:
二阶线性常系数齐次微分方程y″+2y=0的通解为____.答案:解析:
-
第17题:
设y1、y2是二阶常系数线性齐次方程y"+p1y'十p2y=0的两个特解,C1、C2为两个任意常数,则下列命题中正确的是()A.C1y1+C2y2为该方程的通解
B.C1y1+C2y2不可能是该方程的通解
C.C1y1+C2y2为该方程的解
D.C1y1+C2y2不是该方程的解答案:C解析:由线性方程解的结构定理知应选C.仅当y1、y2为线性无关特解时,A才正确. -
第18题:
线性微分方程的各项系数为常数时,称为定常系统。
正确答案:正确 -
第19题:
单选题若二阶常系数线性齐次微分方程y″+ay′+by=0的通解为y=(C1+C2x)ex,则非齐次方程y″+ay′+by=x满足条件y(0)=2,y′(0)=0的解为y=( )。Axex+x2+2
B-xex+x2+2
C-xex+x+2
D-xex+x
正确答案: C解析:
由题意可知,r=1是已知齐次方程对应的特征方程的二重根,则该特征方程为(r-1)2=r2-2r+1=0,齐次方程为y″-2y′+y=0设y*=Ax+B为已知非齐次方程y″-2y′+y=x的特解,代入y″-2y′+y=x得0-2A+Ax+B=x,则A=1,B=2A=2。故已知非齐次方程的通解为y=(C1+C2x)ex+x+2。又y(0)=2,y′(0)=0,代入以上通解得C1=0,C2=-1。故所求方程特解为y=-xex+x+2。 -
第20题:
填空题已知某二阶非齐次线性微分方程的三个解分别为y1=ex,y2=xex,y3=x2ex,则它的通解为____。正确答案: y=C1(x-1)ex+C2(x2-1)ex+ex解析:
因为y1=ex,y2=xex,y3=x2ex是二阶非齐次微分方程的特解,故xex-ex,x2ex-ex是该微分方程对应齐次微分方程的两个线性无关的解。故二阶非齐次微分方程的通解为y=C1(xex-ex)+C2(x2ex-ex)+ex,化简可得y=C1(x-1)ex+C2(x2-1)ex+ex。 -
第21题:
单选题二阶常系数非齐次线性微分方程y″-4y′+3y=2e2x的通解为y=( )。AC1x+C2x3+2e2x(其中C1,C2为任意常数)
BC1x+C2x3-2e2x(其中C1,C2为任意常数)
CC1ex+C2e3x-2e2x(其中C1,C2为任意常数)
DC1ex+C2e3x+2e2x(其中C1,C2为任意常数)
正确答案: A解析:
原微分方程为y″-4y′+3y=2e2x,对应齐次方程y″-4y′+3y=0的特征方程为r2-4r+3=0,特征根为r1=1,r2=3。故原方程所对应齐次方程的通解为y=C1ex+C2e3x。设y*=Ae2x是原方程的特解,代入原方程解得A=-2,故原方程的通解为y=C1ex+C2e3x-2e2x,其中C1,C2为任意常数。 -
第22题:
填空题设y1=3+x2,y2=3+x2+e-x是某二阶线性非齐次微分方程的两个特解,且相应的齐次方程有一个解为y3=x,则该方程的通解为____。正确答案: y=3+x2+c1x+c2e-x解析:
由解的叠加原理可知,y2-y1=e-x是原方程对应齐次方程的一个特解,可知该特解与题中给出的y3=x线性无关,则原方程的通解为y=3+x2+c1x+c2e-x。 -
第23题:
判断题线性微分方程的各项系数为常数时,称为定常系统。A对
B错
正确答案: 错解析: 暂无解析
