求两条异面直线所成的角的大小与在空间内选取的点的位置有关.

题目

求两条异面直线所成的角的大小与在空间内选取的点的位置有关.

相似考题

1.测角前方交汇点的精度与测角误差大小有关,与未知点相对于已知点的位置无关。()此题为判断题(对，错)。

2.（Ⅱ）设M为线段DE的中点，求直线FM与平面A′DE所成角的余弦值．

3.（Ⅱ）求直线PB与平面PCD所成角的大小；

4.张老师在学生学了异面直线的定义后，提出如下命题并判断其正确性：(1)在两个平面内的两条直线是异面直线；(2)不在同一个平面内的两条直线是异面直线；(3)不相交的两条直线是异面直线；(4)不同在任何一个平面的两条直线是异面直线．学生通过此类练习，对异面直线的定义中的“不同在任何一个平面的两条直线”的实质有了更深刻的认识．仔细阅读案例，分析张老师运用了什么教学策略？结合自己的教学实践指出该教学策略运用的技巧．

更多“求两条异面直线所成的角的大小与在空间内选取的点的位置有关.”相关问题

  • 第1题：

    在查询直线角度时，其显示数值与()有关。

    A.拾取点顺序

    B.直线与水平线所成角是锐角还是钝角

    C.直线两端点距离有关

    D.直线与竖直线所成角是锐角还是钝角


    正确答案：A

  • 第2题：



    A.两条相交的直线
    B.两条异面直线
    C.两条平行但不重合的直线
    D.两条重合的直线

    答案：B
    解析：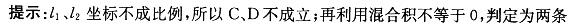

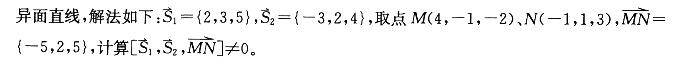
  • 第3题：

    下列四个命题中正确的是（　　）
    ①已知a，6，c三条直线，其中a，b异面，a//c，则b，c异面．
    ②若a与b异面，b与C异面，则a与c异面．
    ③过平面外一点与平面内一点的直线，和平面内不经过该点的直线是异面直线．
    ④不同在任何一个平面内的两条直线叫异面直线．

    A.③④
    B.②③④
    C.①②③④
    D.①②

    答案：A
    解析：
    ①b与c可相交，②a与C可以有平行、相交、异面三种位置关系．(答案为A)

  • 第4题：


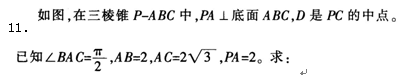
    (1)三棱锥P-ABC的体积；
    (2)异面直线BC与AD所成的角的大小(结果用反三角函数值表示)。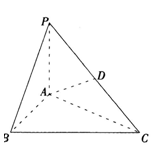



    答案：C
    解析：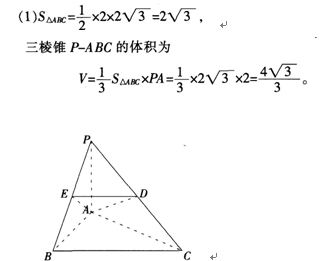

    (2)取PB的中点E，连接DE，AE，则ED／／BC，所以∠ADE加(或其补角)是异面直线BC与
    AD所成的角。
    在三角形ADE中，DE=2，AE=根号2 ，AD=2，

  • 第5题：

    如图，正方体ABCD-A1B1C1D1中，E，F，G分别为AA1，A1D1，BC的中点，则异面直线EF与D1G所成角的大小为__________。



    答案：
    解析：
    连接AD1，AG，由于EF平行于AD1，则异面直线EF与D1G所成角等于AD1与D1G所成角。设正方体棱长为2，在△AD1G中，D1G=3，根据余弦定理，cos∠AD1G=

  • 第6题：

    关于流体静压强特性，正确的说法是（）

    • A、流体静压强的方向与受压面垂直并指向受压面，流体静压强的大小与该点的位置和受压面方向有关
    • B、流体静压强的方向与受压面垂直并背向受压面，流体静压强的大小与该点的位置有关，与受压面方向无关
    • C、流体静压强的方向与受压面垂直并背向受压面，流体静压强的大小与该点的位置和受压面方向有关
    • D、流体静压强的方向与受压面垂直并指向受压面，流体静压强的大小与该点的位置有关，与受压面方向无关

    正确答案:D

  • 第7题：

    在查询直线角度时，其显示数值与（）有关。

    • A、拾取点顺序
    • B、直线与水平线所成角是锐角还是钝角
    • C、直线两端点距离有关
    • D、直线与竖直线所成角是锐角还是钝角

    正确答案:A

  • 第8题：

    压力角是（）上径向直线与齿面在该点处的切平面所夹的锐角。


    正确答案:分度圆

  • 第9题：

    当使用一根绳索起吊设备时，绳索的捆扎点（吊点）必然是在重心位置的上方并且成（），此时起吊是最稳的。

    • A、一条直线
    • B、2°角
    • C、3°角
    • D、5°角

    正确答案:A

  • 第10题：

    单选题
    已知两条直线a，b和平面α，则a∥b的一个充分条件是（　　）．
    A

    a∥α，b∥α

    B

    a，b与α所成的角相等

    C

    a⊥α，b⊥α

    D

    a，b在平面α内的射影平行


    正确答案： A
    解析：
    ABD三项，直线a与直线b平行或相交或异面；C项，由直线与平面垂直的性质可知，两条直线同垂直于一个平面，则这两条直线平行．

  • 第11题：

    单选题
    在查询直线角度时，其显示数值与（）有关。
    A

    拾取点顺序

    B

    直线与水平线所成角是锐角还是钝角

    C

    直线两端点距离有关

    D

    直线与竖直线所成角是锐角还是钝角


    正确答案： C
    解析： 暂无解析

  • 第12题：

    填空题
    压力角是（）上径向直线与齿面在该点处的切平面所夹的锐角。

    正确答案： 分度圆
    解析： 暂无解析

  • 第13题：

    两条直线垂直于同一条直线，这两条直线的关系为（ ）

    A．平行

    B．相交

    C．异面

    D．位置不确定


    正确答案：D

  • 第14题：

    已知两直线则它们的关系是：
    A.两条相交的直线 B.两条异面直线
    C.两条平行但不重合的直线 D.两条重合的直线


    答案：B
    解析：
    提示:l1,l2坐标不成比例，所以C、D不成立，再利用混合积不等于0，判定为两条异面直

  • 第15题：

    分别和两条异面直线AB、CD同时相交的两条直线AC、BD（　　）

    A.相交．
    B.平行．
    C.是异面直线．
    D.垂直．

    答案：C
    解析：

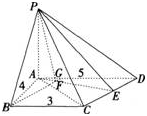
  • 第16题：

    如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90o，E是CD的中点。
    (1)证明：CD⊥平面PAE；
    (2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P-ABCD的体积。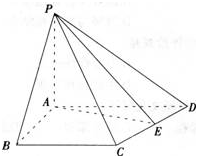


    答案：
    解析：



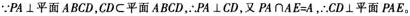
  • 第17题：

    已知A点的磁偏角为西偏18′，过A点的真子午线与中央子午线的收敛角为+3′，直线AB的坐标方位角α=66°22′，求AB直线的真方位角与磁方位角。


    正确答案: （1）A真=α+γ=66°22′+3′=66°25′
    （2）A磁= A真-δ=66°22′+18′=66°43′

  • 第18题：

    已知两条异面直线，直线1过（20.3，0，53.1）和（38.2，40，31.5）两点，直线2过（24.1，81.6，0）和（86.2，37.9，-76.4）两点，求两条异面直线的公垂线长度（）（两异面直线的最短距离）。

    • A、31.0554
    • B、31.0555
    • C、31.0556
    • D、31.0557

    正确答案:B

  • 第19题：

    测角前方交会点的精度与测角误差大小有关，与未知点相对于已知点的位置无关。


    正确答案:错误

  • 第20题：

    徒手画圆角时，先用目测在直角边的分角线上选取圆心位置，使它与角的两边的距离等于圆角的半径大小，过圆心向两边引垂直线定出圆弧的起止点，并在分角线上也定出一个圆周点，然后把这（）连成圆弧即可。

    • A、1个点
    • B、2个点
    • C、3个点
    • D、4个点

    正确答案:C

  • 第21题：

    单选题
    两条异面直线是指（　　）．
    A

    两条不相交的直线

    B

    两条不平行的直线

    C

    不在同一平面内的两条直线

    D

    不在任何一个平面内的两条直线


    正确答案： B
    解析：
    A项，两条直条不相交但可以平行，这两条直线不一定异面；B项，两条不平行的直线可能相交，不一定异面；C项，分别在两平面的直线有可能相交也可能平行；D项，由异面直线定义可知为正确．

  • 第22题：

    单选题
    关于流体静压强特性，正确的说法是（）
    A

    流体静压强的方向与受压面垂直并指向受压面，流体静压强的大小与该点的位置和受压面方向有关

    B

    流体静压强的方向与受压面垂直并背向受压面，流体静压强的大小与该点的位置有关，与受压面方向无关

    C

    流体静压强的方向与受压面垂直并背向受压面，流体静压强的大小与该点的位置和受压面方向有关

    D

    流体静压强的方向与受压面垂直并指向受压面，流体静压强的大小与该点的位置有关，与受压面方向无关


    正确答案： D
    解析： 流体静压强的第一个特性是它的方向垂直受压面并指向受压面；第二个特性是它的大小只与该点的位置有关，而与方向无关，即静止流体内任一点上各方向的静压强均相等。因此正确的答案应是D。

  • 第23题：

    填空题
    在空间中，①若四点不共面．则这四点中任何三点都不共线；②若两条直线没有公共点，则这两条直线是异面直线，以上两个命题中。逆命题为真命题的是____．

    正确答案： ②
    解析：
    ①项，逆命题是若空间四点中任何三点都不共线，则四点不共面。该命题不符合客观实际；②项，其逆命题为若两条直线是异面直线，则两条直线没有公共点。该命题符合客观实际．

  • 第24题：

    单选题
    已知空间两条直线a、b和平面M，则a∥b的充分条件是（　　）．
    A

    a∥M，b∥M

    B

    a、b与M所成的角相等

    C

    a⊥M，b⊥M

    D

    a、b在M内的射影平行


    正确答案： C
    解析：
    A项，a∥M，b∥M，但a、b还可能相交；B项，a、b可能和M相交于同一点； C项，由直线和平面垂直的性质定理知，a∥b．

相关内容