曲线y=x^3+x-2在点(1,0)处的切线方程是()A、y=2(x-1)B、y=4(x-1)C、y=4x-1D、y=3(x-1)
题目
曲线y=x^3+x-2在点(1,0)处的切线方程是()
A、y=2(x-1)
B、y=4(x-1)
C、y=4x-1
D、y=3(x-1)
相似考题
更多“曲线y=x^3+x-2在点(1,0)处的切线方程是() ”相关问题
-
第1题:
曲线y=sin(x+1)在点(-1,0)处的切线斜率为______.答案:解析:填1.因为y'=cos(x+1),则y'(-1)=1. -
第2题:
曲线y=x3-x在点(1,0)处的切线方程y=______.答案:解析:填2(x-1).因为y'=3x2-1,y'(1)=2,则切线方程为y=2(x-1). -
第3题:
(I)求曲线y=Inx在(1,0)点处的切线方程.
(Ⅱ)并判定在(0,+∞)上的增减性.答案:解析:
-
第4题:
曲线y=2x2在点(1,2)处的切线方程y=______.答案:解析: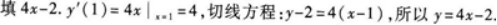
-
第5题:
曲线sin(xy)+ln(y-x)=x在点(0,1)处的切线方程是________.答案:1、y=x+1.解析:先求曲线sin(xy)+ln(y-x)=x在点(0,1)处切线斜率y'(0).等式sin(xy)+ln(y-x)=x两端对x求导得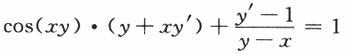
在上式中令x=0,y=1得y'(0)=1,于是该曲线在点(0,1)处的切线方程为y-1=x,即y=x+1.
