图示质量为m，半径为r的定滑轮O上绕有细绳，依靠摩擦使绳在轮上不打滑，并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为a，0

题目
图示质量为m，半径为r的定滑轮O上绕有细绳，依靠摩擦使绳在轮上不打滑，并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为a，0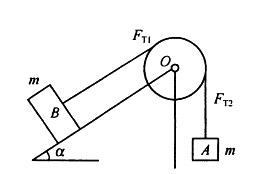

相似考题

1.小物块质量为m在转动的圆桌上，其离心力转轴的距离为r，如图所示。设物块与圆桌之间的摩擦系数为μ，为使物块不产生滑动，则最大速度不应超过（　　）。

2.一绳索跨过匀质滑轮B，绳的一端挂一重物A；另一端缠绕一匀质圆柱C，如图所示。已知重物A的质量为mA；定滑轮B和圆柱C的质量分别为mB和mC，它们的半径均为r。绳的质量略去不计，它对定滑轮无相对滑动。设mB=mC=2mA，则定滑轮与圆柱之间绳索的拉力T为( )。

3.图示两重物的质量均为m，分别系在两软绳上。此两绳又分别绕在半径各为r与2r，并固结在一起的两圆轮上。两圆轮构成的鼓轮的质量亦为m，对轴O的回转半径为ρ0外。两重物中一铅垂悬挂，一置于光滑平面上。当系统在左重物重力作用下运动时，鼓轮的角加速度α为：

4.图示在倾角为α的光滑斜面上置一弹性系数为k的弹簧，一质量为m的物块沿斜面下滑s距离与弹簧相碰，碰后弹簧与物块不分离并发生振动，则自由振动的固有圆频率应为：A. (k/m)1/2 B.[k/(ms)]1/2 C. [k/(msinα)]1/2 D. (ksinα/m)1/2

参考答案和解析
答案：B
解析：
在右侧物重力作用下，滑轮顺时针方向转动，故轮上作用的合力矩应有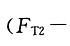
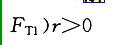
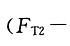
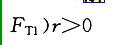
答案:B
更多“图示质量为m，半径为r的定滑轮O上绕有细绳，依靠摩擦使绳在轮上不打滑，并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾角为a，0 ”相关问题

  • 第1题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计质量的软绳上，绳绕过勻质定滑轮，滑轮半径为r，质量为m，则此滑轮系统对转轴O之动量矩为：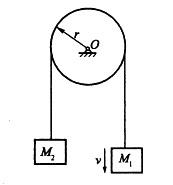



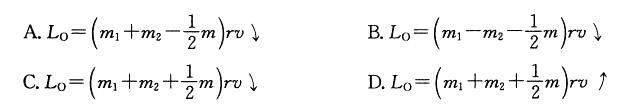    答案：C
    解析：
    根据动量矩定义和公式：Lo=Mo(m1v)+Mo(m2v)+Jo轮ω

  • 第2题：

    图示质量为m，半径为r的定滑轮O上绕有细绳，依靠摩擦使绳在轮上不打滑，并带动滑轮转动。绳之两端均系质量m的物块A与B。块B放置的光滑斜面倾斜角为α，0T1和FT2的大小有关系：

    A. FT1= FT2 B.FT1T2 C. FT1>FT2 D.只依据已知条件则不能确定


    答案：B
    解析：
    提示:根据动量矩定理求力。

  • 第3题：

    图示均质圆轮，质量m，半径R，由挂在绳上的重为W的物块使其绕质心轴O转动。设重物的速度为v，不计绳重，则系统动量、动能的大小是（　　）。




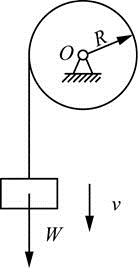
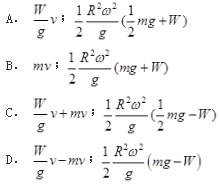    答案：A
    解析：

  • 第4题：

    图示圆轮上绕一细绳，绳端悬挂物块。物块的速度v、加速度a。圆轮与绳的直线段相 切之点为P，该点速度与加速度的大小分别为：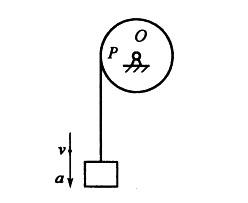



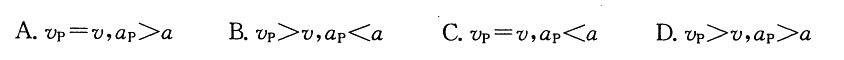    答案：A
    解析：
    定轴转动刚体上P点与绳直线段的速度和切向加速度相同，而P点还有法向加速度。
    答案:A

  • 第5题：

    质量为m，半径为r 的定滑轮O 上绕有细绳。依靠摩擦使绳在轮上不打滑，并带动滑轮转动。绳之两端均系质量m 的物块A 与B。块B放置的光滑斜面倾角为α 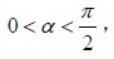，假定定滑轮O 的轴承光滑，当系统在两物块的重力作用下开始运动时，B与O间，A 与O
    间的绳力FT1和FT2的大小有关系：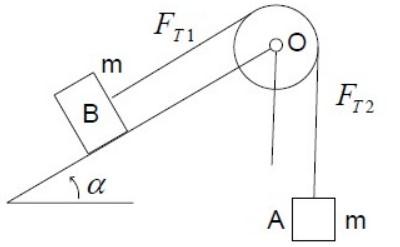

    （A） FT1=FT2
    （B） FT1 T2
    （C） FT1 >FT2
    （D）只根据已知条件不能确定


    答案：B
    解析：
    解：选B。
    此题的关键处在于：绳在滑轮上是有摩擦的，因此FT1 =FT2
    因为在重力作用下，物块 A 向下运动，列受力表达式（两物块加速度大小和速度大小均相同）可得，FT1 T2。

  • 第6题：

    两重物的质量均为m，分别系在两软绳上，此两绳又分别绕在半径各为r与2r并固结一起的两圆轮上，两圆轮构成之鼓轮的质量亦为m,对轴O的回转半径为p0,两重物中一铅垂悬挂，一置于光滑平面上，当系统在左重物重力作用下运动时，鼓轮的角加速度a为：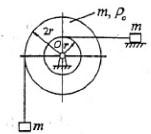



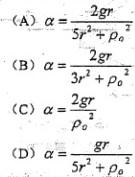    答案：A
    解析：
    均匀细直杆对一端的转动惯量：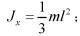
    均匀细直杆对垂直与杆的中心轴的转动惯量：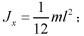
    匀质圆板对垂直于板的中心轴的转动惯量：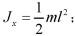
    惯性半径：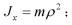
    作受力分析，下降的重物：mg-T1=ma1,水平方向上的重物T2=ma2;
    又 a1 = 2ar, a2 = ar。再根据动量矩定理，联列以上方程得选项（A）。

  • 第7题：

    如图半径为R的滑轮上绕一绳子，绳与轮间无相对滑动。绳子一端挂一物块，在图示位置物块有速度和加速度。M点为滑轮上与铅垂绳段的相切点，则在此瞬时M点加速度的大小为（　　）。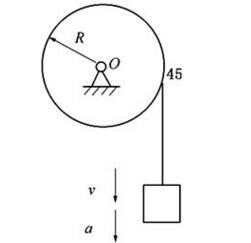



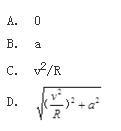    答案：C
    解析：

  • 第8题：

    如图8-2所示，物块A放在水平的光滑桌面上，用细绳的一端系住A绳穿过小孔O，另一端系物块B．当A在桌面上以角速度ω=5 rad/s绕O做匀速圆周运动时，绳被拉紧，B静止才动．已知A的质量mA=1 kg，A离O的距离为1 m，则B的质量等于（　　）（取g=10 m/s2）


    A.2.5 kg
    B.2 kg
    C.1.5 kg
    D.0.5 kg

    答案：A
    解析：
    本试题考查的知识点是牛顿定律和圆周运动的向心力． A、B用一根细线系在两端，当细线拉紧时，线上各点的张力相等．A受细线拉力FA作用，B受重力G和细线拉力FB的作用，A的重力和桌面的支持力抵消，不予考虑．FA=FB=F．A做匀速圆周运动，它的向心力就是细线拉力F．B静止不动．
    对A、B写出牛顿方程有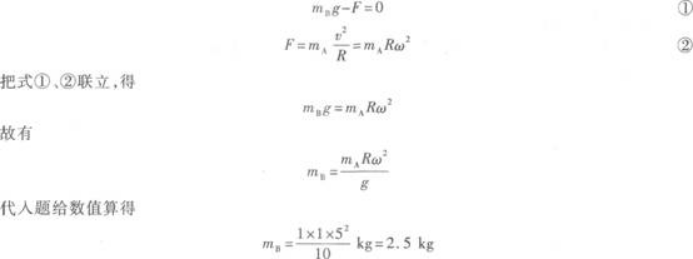

  • 第9题：

    确定物体绕某个轴的转动惯量，可以由理论计算也可通过实验测定。
    (1)用积分计算质量为m，半径为R的均质薄圆盘绕其中心轴的转动惯量。
    (2)该圆盘质量未知，可用如图9所示的实验方法测得该圆盘绕中心轴的转动惯量。在圆盘的边缘绕有质量不计的细绳，绳的下端挂一质量为m的重物，圆盘与转轴间的摩擦忽略不计。测得重物下落的加速度为a，求圆盘绕其中心轴的转动惯量。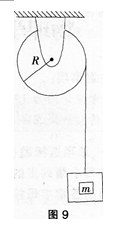


    答案：
    解析：

  • 第10题：

    如图4-63所示，两重物m1和m2的质量分别为m1和m2，两重物系在不计质量的软绳上，绳绕过均质定滑轮，滑轮半径为r,质量为M,则此滑轮系统对转轴O之动量矩为（）。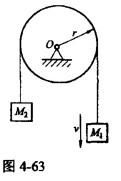



    答案：C
    解析：
    提示：根据动量矩定义和公式

  • 第11题：

    半径为R具有光滑轴的定滑轮边缘绕一细绳，绳的下端挂一质量为m的物体绳的质量可以忽略，绳与定滑轮之间无相对滑动若物体下落的加速度为a，则定滑轮对轴的转动惯量J＝（）。


    正确答案:m（g-a）R2/a

  • 第12题：

    单选题
    质量为2m，半径为R的偏心圆板可绕通过中心O的轴转动，偏心距OC＝ 。在OC连线上的A点固结一质量为m的质点，OA＝R如图示。当板以角速度w绕轴O转动时，系统动量K的大小为（）。（注：C为圆板的质心）。
    A

    K＝0

    B

    K＝mRw

    C

    K＝mRw

    D

    K＝2mRw


    正确答案： A
    解析： 暂无解析

  • 第13题：

    均质圆盘质量为m，半径为R，在铅垂平面内绕O轴转动，图示瞬时角速度为ω，则其对O轴的动量矩和动能大小分别为：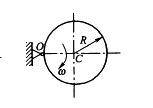



    答案：D
    解析：

  • 第14题：

    圆轮上绕一细绳，绳端悬挂物块，物块的速度为v、加速度a,圆轮与物块的直线段相切之点为P，该点速度与加速度的大小分别为：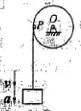

    (A)vp=v,ap＞a
    (B)vp＞v,ap＜a
    (C)vp=v,ap＜a
    (D)vp＞v,ap＞a


    答案：A
    解析：
    速度肯定是和物块速度保持一致，加速度的大小是大于物块的。

  • 第15题：

    两重物的质量均为m，分别系在两软绳上。此两绳又分别绕在半径各为r与2r并固结在一起的两轮上。两圆轮构成之鼓轮的质量亦为m，对轴O的回转半径为ρO。两重物中一铅垂悬挂，一置于光滑平面上。当系统在左重物重力作用下运动时，鼓轮的角加速度α为：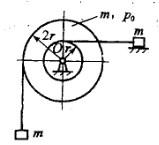



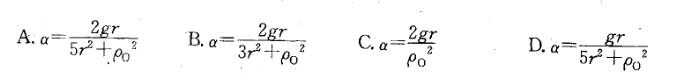    答案：A
    解析：

  • 第16题：

    圆轮上绕一细绳，绳端悬挂物块。物块的速度v、加速度a。圆轮与绳的直线段相切之点为P，该点速度与加速度的大小分别为：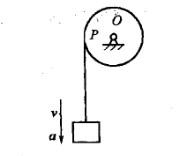

    A. vp = v，ap>a B. vp>v，apC. vp =v，app>v，ap>a


    答案：A
    解析：
    提示:定轴转动刚体上P点与绳直线段的速度和切向加速度相同，而P点还有法向加速度。

  • 第17题：

    各重为P的两物块A和B用绳连接并将此绳缠绕在均质滑轮O上，如图所示，如滑轮半径为R，重为Q，角速度为ω，则系统对O轮的动量矩为（　　）。


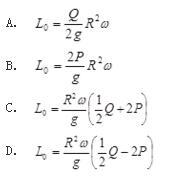    答案：C
    解析：
    系统对O轮的动量矩为物体A、B以及滑轮对O的动量矩的矢量和，因三个动量矩均为逆时针方向，因此，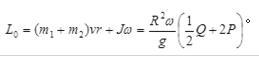

  • 第18题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统的动量为：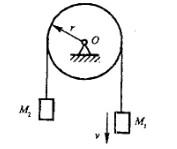



    答案：B
    解析：
    提示:根据动量的定义p=∑mivi。

  • 第19题：

    图示鼓轮半径r=3.65m，对转轴O的转动惯量JO= 0.92kg ? m2；绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦，欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物，需对鼓轮作用的转矩M的大小是：

    A. 37.8N ? m B. 47N ? m
    C. 36.3N ? m D. 45.5N ? m


    答案：B
    解析：
    提示:动量矩定理(JO +mr2 )α=M-mgr。

  • 第20题：

    如图所示的装置中，物块A、B、C的质量分别为M、m和mo，物块曰放置在物块A上，物块A用不可伸长的轻绳通过滑轮与物块C连接，绳与滑轮之间的摩擦不计。若日随A一起沿水平桌面做匀速运动，则可以断定(重力加速度为9)（　　）。



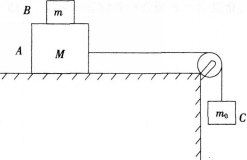    A．物块A与桌面之间有摩擦力，大小为，mog

    B．物块A与B之间有摩擦力.大小为mog

    C．桌面与A之间，B与A之间，都有摩擦力，两者方向相同，它们的合力为mog

    D．桌面与A之间，B与A之间，都有摩擦力，两者方向相反，它们的合力为meg

    答案：A
    解析：
    对B分析，B受重力、支持力，因B水平方向不受外力，故B不会受到A对B的摩擦力，故AB间没有摩擦力，BCD均错误；对AB整体受力分析可知，整体受绳的拉力、重力、支持力，要使整体做匀速直线运动，A应受到地面对其向左的摩擦力，大小与绳子的拉力相同；对C分析，可知C受重力与绳子的拉力而处于匀速运动状态，故绳子的拉力为mog；由此可知，物体A与桌面间的摩擦力大小为mog；故A正确。

  • 第21题：

    如图所示，两重物M1和M2的质量分别为m1和m2，两重物系在不计重量的软绳上，绳绕过均质定滑轮，滑轮半径r，质量为M，则此滑轮系统对转轴O之动量矩为：



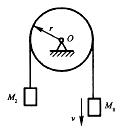    答案：C
    解析：
    提示 根据动量矩定义和公式:LO= MO(m1v) + MO(m2v)+JO轮w。

  • 第22题：

    圆柱体定滑轮的质量为m，半径为R，绕其质心轴转动的角位移为θ=a+bt+ct2，a、b、c为常数，作用在定滑轮上的力矩为（）

    • A、（1/2）maR2
    • B、bmR2
    • C、（1/2）mbR2
    • D、mcR2

    正确答案:D

  • 第23题：

    单选题
    图示鼓轮半径r=3.65m，对转轴O的转动惯量Jo=0.92kg·m 2；绕在鼓轮上的绳端挂有质量m=30kg的物体A。不计系统质量与摩擦，欲使鼓轮以角加速度α=37.8rad/s2转动来提升重物，需对鼓轮作用的转矩M的大小是：（）
    A

    37.8N.m

    B

    47N.m

    C

    36.3N.m

    D

    45.5N.m


    正确答案： C
    解析： 暂无解析

相关内容