函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程的( )。A.通解 B.特解 C.不是解 D.是解，但不是通解也不是特解

题目
函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程



的( )。

A.通解
B.特解
C.不是解
D.是解，但不是通解也不是特解
相似考题

1.若 Normal 0 7.8 磅 0 2 false false false EN-US ZH-CN X-NONE MicrosoftInternetExplorer4 y1·y2为二阶线性常系数微分方程y〞+p1y＇+p2y=0的两个特解，则C1y1+C2y2（）.A.为所给方程的解，但不是通解B.为所给方程的解，但不一定是通解C.为所给方程的通解D.不为所给方程的解

2.微分方程y''=(y')2的通解是： A. lnx+c B. ln(x+c) C. c2+ln x+c1 D. c2-lnlx+c1 (以上各式中，c1、c2为任意常数）

3.一种解？ A通解 B.特解 C.不是解 D.是解，但不是通解也不是特解

4.微分方程y''+2y=0的通解是：(A,B为任意常数）

参考答案和解析
答案：D
解析：
y=c1e2x+c2=c3e2x经验证是方程的解，但不是通解也不是特解
更多“函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程 的( )。A.通解 B.特解 C.不是解 D.是解，但不是通解也不是特解”相关问题

  • 第1题：


    A、 通解
    B、 特解
    C、 不是解
    D、 解，既不是通解又不是特解

    答案：D
    解析：

  • 第2题：


    A.是此方程的解，但不一定是它的通解
    B.不是此方程的解
    C.是此方程的特解
    D.是此方程的通解

    答案：D
    解析：

  • 第3题：

    在下列微分方程中，以函数y＝C1e^－x＋C2e^4x（C1，C2为任意常数）为通解的微分方程是（　　）。

    A． y″＋3y′－4y＝0
    B． y″－3y′－4y＝0
    C． y″＋3y′＋4y＝0
    D． y″＋y′－4y＝0

    答案：B
    解析：

    由题意知，二阶常系数齐次线性微分方程的特征方程的两个根为－1和4，只有B项满足。
    【总结】求二阶常系数齐次线性微分方程y″＋py′＋qy＝0的通解的步骤：
    ①写出微分方程的特征方程r2＋pr＋q＝0；
    ②求出特征方程的两个根r1，r2；
    ③根据r1，r2的不同情形，写出微分方程的通解：
    a．当r1≠r2，



    b．当r1＝r2，



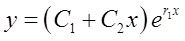
    c．一对共轭复根r1，2＝α±βi，y＝eαx（C1cosβx＋C2sinβx）。

  • 第4题：

    微分方程y''=(y')2的通解是：

    A. lnx+c
    B. ln(x+c)
    C. c2+ln x+c1
    D. c2-lnlx+c1
    （以上各式中，c1、c2为任意常数）

    答案：D
    解析：
    提示 此题为可降阶的高阶微分方程，按方程不显含变量y计算。


    y=c2-lnlx+c1 。

  • 第5题：

    的哪一种解？

    A.通解
    B.特解
    C.不是解
    D.是解，但不是通解也不是特解

    答案：D
    解析：

  • 第6题：

    微分方程y''-4y=4的通解是（ ）（C1,C2为任意常数)。


    答案：B
    解析：
    提示：显然C不是通解；对应齐次方程的通解为C1e2x+C2e-2x ,y=-1是一个特解，故应选B。

  • 第7题：

    设y1、y2是二阶常系数线性齐次方程y"+p1y'十p2y=0的两个特解，C1、C2为两个任意常数，则下列命题中正确的是（）

    A.C1y1+C2y2为该方程的通解
    B.C1y1+C2y2不可能是该方程的通解
    C.C1y1+C2y2为该方程的解
    D.C1y1+C2y2不是该方程的解

    答案：C
    解析：
    由线性方程解的结构定理知应选C．仅当y1、y2为线性无关特解时，A才正确．

  • 第8题：

    微分方程y"=y’2的通解是（）（C1、C2为任意常数）。

    • A、lnx+C
    • B、ln（x+C）
    • C、C2+ln
    • D、C2-ln

    正确答案:D

  • 第9题：

    单选题
    微分方程y"=y’2的通解是（）（C1、C2为任意常数）。
    A

    lnx+C

    B

    ln（x+C）

    C

    C2+ln

    D

    C2-ln


    正确答案： C
    解析： 暂无解析

  • 第10题：

    单选题
    设函数y1，y2，y3都是线性非齐次方程y″＋p（x）y′＋q（x）y＝f（x）的不相等的特解，则函数y＝（1－c1－c2）y1＋c1y2＋c2y3（　　）。（c1，c2为任意常数）
    A

    是所给方程的通解

    B

    不是方程的解

    C

    是所给方程的特解

    D

    可能是方程的通解，但一定不是其特解


    正确答案： C
    解析：
    由于y1，y2，y3都是y″＋p（x）y′＋q（x）y＝f（x）的不相等的特解，则y2－y1，y3－y1是它对应的齐次方程的特解，故y＝（1－c1－c2）y1＋c1y2＋c2y3＝y1＋c1（y2－y1）＋c2（y3－y1）是非齐次方程y″＋p（x）y′＋q（x）y＝f（x）的解，但是，由于无法确定y2－y1与y3－y1是否为线性无关，故不能肯定它是y″＋p（x）y′＋q（x）y＝f（x）的通解。

  • 第11题：

    单选题
    函数（C1，C2为任意数）是微分方程y″－y′－2y＝0的（　　）。[2014年真题]
    A

    通解

    B

    特解

    C

    不是解

    D

    解，既不是通解又不是特解


    正确答案： B
    解析：
    微分方程y″－y′－2y＝0的特征方程为：r2－r－2＝0，解特征方程得：r1＝2，r2＝－1。故其通解为：y＝C1e2x＋C2e－x，即题中函数是方程的解，但不是通解或特解。

  • 第12题：


    A．通解
    B．特解
    C．不是解
    D．既不是通解又不是特解，而是解

    答案：D
    解析：

  • 第13题：

    微分方程y''=x+sinx的通解是（c1，c2为任意常数）：


    答案：B
    解析：
    提示 本题为可降阶的高阶微分方程，连续积分二次，得通解。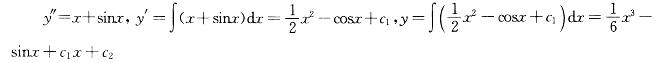

  • 第14题：

    函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程



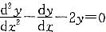
    的( )。

    A.通解
    B.特解
    C.不是解
    D.是解，但不是通解也不是特解

    答案：D
    解析：
    y=c1e2x+c2=c3e2x经验证是方程的解，但不是通解也不是特解

  • 第15题：

    已知微分方程y'+p（x）y = q（x）[q（x）≠0]有两个不同的特解y1（x）， y2（x），C为任意常数，则该微分方程的通解是：

    A.y=C（y1-y2）
    B. y=C（y1+y2）
    C. y=y1+C（y1+y2）
    D. y=y1+C（y1-y2）

    答案：D
    解析：
    提示：y'+p（x）y=q（x），y1（x）-y2 （x）为对应齐次方程的解。微分方程：y'+p（x）=q（x）的通解为：y=y1+C（y1 -y2）。

  • 第16题：


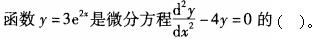    A.通解
    B.特解
    C.是解，但既非通解也非特解
    D.不是解

    答案：B
    解析：
    代入检验。

  • 第17题：

    微分方程y''=y'2的通解是（ ）（C1、C2为任意常数）。


    答案：D
    解析：
    提示：这是不显含y可降阶微分方程，令p=y',则dp/dx=y'',用分离变量法求解得，-y'=1/(x+C1) ，两边积分，可得y=C2-ln x+C1 ，故应选D,也可采用检验的方式。

  • 第18题：

    微分方程的含有任意常数的解是该微分方程的通解。


    正确答案:正确

  • 第19题：

    函数是微分方程的（）。

    • A、通解
    • B、特解
    • C、是解，但既非通解也非特解
    • D、不是解

    正确答案:B

  • 第20题：

    判断题
    微分方程的含有任意常数的解是该微分方程的通解。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第21题：

    单选题
    函数是微分方程的（）。
    A

    通解

    B

    特解

    C

    是解，但既非通解也非特解

    D

    不是解


    正确答案： A
    解析： 暂无解析

相关内容