双曲线x2-y2/2 =1在点(-√2,√2)处的切线的方程是( ).(A)y=-x+√2.(B)y=-x+3√2.(C)y=-2x-√2.(D)y=-2x+3√2.

题目

双曲线x2-y2/2 =1在点(-√2,√2)处的切线的方程是( ).

(A)y=-x+√2.

(B)y=-x+3√2.

(C)y=-2x-√2.

(D)y=-2x+3√2.

相似考题

1.曲线y=2＋lnx在点x=1处的切线方程是()A、y=x-1B、y=x+1C、y=xD、y=-x

2.曲线y=x3+1在点（1，2）处的切线方程是__________．

3.曲线y=x3—2x在点（1，-1）处的切线方程为 ．

4.曲线y=x^3＋x－2在点(1,0)处的切线方程是()A、y=2(x-1)B、y=4(x-1)C、y=4x-1D、y=3(x-1)

更多“双曲线x2-y2/2 =1在点(-√2,√2)处的切线的方程是( ).(A)y=-x+√2.(B)y=-x+3√2.(C)y=-2x-√2.(D)y=-2x+3√2.”相关问题

  • 第1题：

    曲线y=x3-5x+l在点（2，-l）处的切线方程为 （ ）

    A.7x—Y一15—0

    B.7x-Y+15=0

    C.x+y-1=0

    D.z+y+1=0


    正确答案：A
    本题主要考查的知识点为曲线的切线方程．【应试指导】y=x3-5x+1在点(2，-l)处的切线的斜率为

  • 第2题：

    如果曲线y=f(x)在点（x,y）处的切线斜率与x2成正比，并且此曲线过点（1，-3）和（2，11），则此曲线方程为（ ）。

    A. y=x3-2

    B. y=2x3-5

    C. y=x2-2

    D. y=2x2-5


    正确答案：B

    由曲线过点（1，-3）排除A、C项。由此曲线过点（2，11）排除D，故选B。y=2x3-5显然过点（1,-3）和（2，11），且它在（x,y）处的切线斜率为6x2，显然满足与x2成正比。

  • 第3题：

    曲线y=x4-3在点(1，-2)处的切线方程为（）

    A.2x-y-6=0
    B.4x-y-6=0
    C.4x-y-2=0
    D.2x-y-4=0

    答案：B
    解析：
    【考情点拨】本题考查了曲线上一点处的切线方程的知识点．

  • 第4题：

    曲线y=e2x-4x在点(0，1)处的切线方程是（）

    A.2x-y-1=0
    B.2x+y-1=0
    C.2x-y+1=0
    D.2x+y+1=0

    答案：B
    解析：
    【考情点拨】本题考查了曲线的切线方程的知识点．

  • 第5题：

    曲线y=x3-4x+2在点(1，-l)处的切线方程为()

    A.x-y-2=0
    B.x-y=0
    C.x+y=0
    D.27+y-2=0

    答案：C
    解析：

  • 第6题：

    过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是（ ）。

    A.(x-3)2+(y+1)2=4
    B.(x+3)2+(y-1)2=4
    C.(x-1)2+(y-1)2=4
    D.(x+1)2+(y+1)2=4

    答案：C
    解析：

  • 第7题：

    设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。

    A.
    B.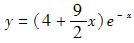
    C.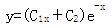
    D.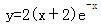

    答案：D
    解析：

  • 第8题：

    曲线y=3x+1在点(1，3)处的切线方程为( )。

    A、y=2x+1
    B、r=4x-1
    C、y=4x+2
    D、y=3x

    答案：B
    解析：
    先求出y=x3+1在点(1，3)处切线的斜率为4，再根据过(1，3)，得到切线方程为y=4x-l。

  • 第9题：

    填空题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。

    正确答案： y=-exsin2x
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

  • 第10题：

    填空题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

    正确答案： x-y=0
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第11题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第12题：

    单选题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。
    A

    y＝exsin2x

    B

    y＝－exsin2x

    C

    y＝exsinx

    D

    y＝－exsinx


    正确答案： B
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

  • 第13题：

    曲线y＝x2＋1在点(1，2)处的切线方程为__________．


    正确答案：
    y＝2x

  • 第14题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第15题：

    曲线x2+y2=2x在点(1，1)处的切线方程为.


    答案：
    解析：
    【答案】y=1【考情点拨】本题考查了曲线上一点处的切线方程的知识点．
    【应试指导】由x2+y2=2x，两边对x求导得2x+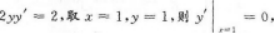

  • 第16题：

    曲线y=2x2在点(1，2)处的切线方程y=______．


    答案：
    解析：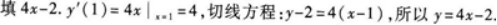

  • 第17题：

    曲线y＝x3＋2x－1在点M(1，2)处的切线方程是

    A.5x－y－3＝0
    B.x－5y－3＝0
    C.5x＋y－3＝0
    D.x＋5y－3＝0

    答案：A
    解析：

  • 第18题：

    曲线y=x3-4x+2在点(1，-1)处的切线方程为（　　）

    A.x-y-2-0
    B.x-y=0
    C.x+y=0
    D.x+y-2=0

    答案：C
    解析：

  • 第19题：

    曲线y=χ3+2χ-1在点(1，2)处的切线方程为( )。

    A、5χ-y-3=0
    B、14χ-y-12=0
    C、5χ-y+3=0
    D、14χ+y-12=0

    答案：A
    解析：
    由已知得y'=3x2+2，则其在(1，2)处切线的斜率为k=5，又切线过点(1，2)则其方程为5x— y-3=0。

  • 第20题：

    过z轴和点(1，2，-1)的平面方程是（ ）。
    A. x + 2y-z-6 = 0 B. 2x-y = 0 C.y+ 2z = 0 D. x+ z = 0


    答案：B
    解析：
    正确答案是B。
    提示：过z轴的平面方程为Ax+By=0,再将点(1，2，-1)代入确定A和B的值则可。

  • 第21题：

    单选题
    已知y＝x/lnx是微分方程y′＝y/x＋φ（x/y）的解，则φ（x/y）的表达式为（　　）。
    A

    －y2/x2

    B

    y2/x2

    C

    －x2/y2

    D

    x2/y2


    正确答案： B
    解析：
    将y＝x/lnx代入微分方程得（lnx－1）/ln2x＝1/lnx＋φ（x/y）。故φ（x/y）＝－1/ln2x＝－1/（x/y）2＝－y2/x2。

  • 第22题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    －x－y＝0

    B

    x－y－1＝0

    C

    x－y＝0

    D

    x＋y＝0


    正确答案： A
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第23题：

    单选题
    曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为（　　）。
    A

    y＝excos2x

    B

    y＝－excos2x

    C

    y＝exsin2x

    D

    y＝－exsin2x


    正确答案： A
    解析：
    所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r2－2r＋5＝0，解得r1，2＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝ex（c1cos2x＋c2sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝ex（c1cos2x＋c2sin2x）得c1＝0，c2＝－1。故所求曲线方程为y＝－exsin2x。

相关内容